3. 制御で用いられる関数
ここでは、制御工学の中で良く用いられる主要な関数を挙げる。
- インパルス関数
- 指数関数
- ステップ関数
- 正弦波関数
- ランプ関数
- 指数関数重み付き正弦波関数
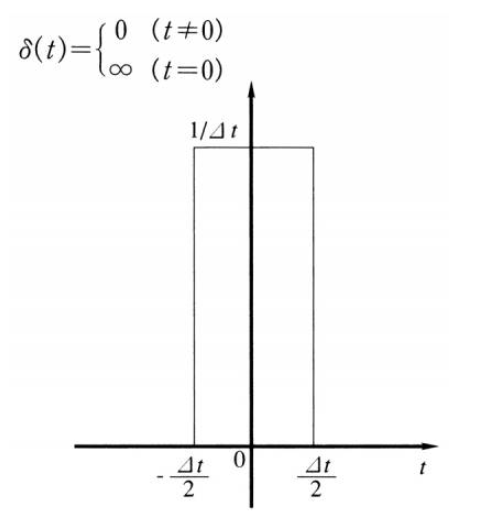
図のように時刻t=0において微少時間Δtのあいだだけ存在する高さ1/Δtの関数y(t)において、Δt→0としたときに得られる極限関数のことをインパルス関数(または、デルタ関数)という。以下のような性質をもつ。
$$\delta(t)=\begin{cases} \infty \enspace (t=0) \\ 0 \enspace \enspace (t \neq 0)\end{cases}$$ $$\int_{-\infty}^{\infty} \delta(t) dt =1 $$ $$\delta(t - \tau)=\begin{cases} \infty \enspace (t=\tau) \\ 0 \enspace \enspace (t \neq \tau)\end{cases} $$ $$\int_{- \infty}^{\infty} f(t) \delta(t- \tau)dt=f(\tau)$$
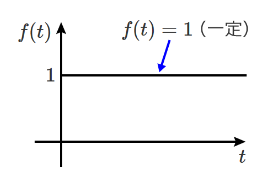
$$f(t)=\begin{cases} 0 \enspace \enspace (t \lt 0) \\ 1 \enspace \enspace (t \geq 0)\end{cases}$$ で表わされる関数をステップ関数という。
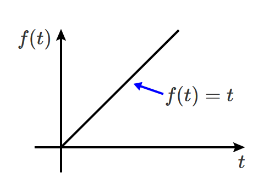
$$f(t)=at$$ で表せる関数をランプ関数という。
*指数関数 \(e^{at}\)
$$\frac{d e^{at}}{dt}=a e^{at}$$ $$\int e^{at}dt=\frac{1}{a} e^{at} $$
*正弦波関数 \( f(t)=A\sin (\omega t + \theta) \)
\(A\):振幅
\(\omega\):角周波数
\(\theta\):初期位相
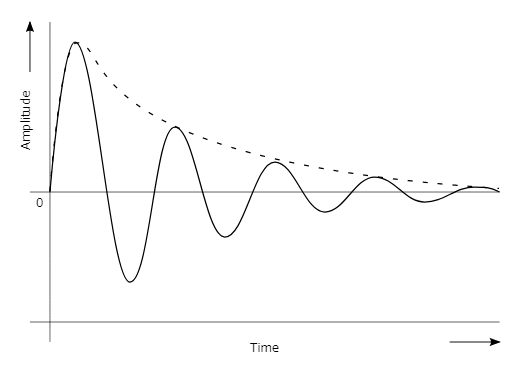
*指数関数重み付き正弦波関数
$$ f(t)=e^{at}\sin (\omega t + \theta) $$


“3. 制御で用いられる関数” に対して1件のコメントがあります。
コメントは受け付けていません。