11. インパルス応答
動的システムの時間応答を知りたい場合、次の方法が考えられる。
1)実システムに実入力を加えて出力応答を実験的に観測する。
2)数式モデルを基に計算で求める。
1)の場合、問題点として、コストがかかる、実験が難しい場合が多い、危険が伴う(システムが不安定だと暴走)、等があるが、製品試作の最終段階では重要である。2)の場合、様々な入力に対する時間応答が容易に求まる利点があるが、一般には数式モデルが実システムを正確に反映していないと駄目である。(ただし、簡略した数式モデルで傾向を把握することで済む場合もある。)
2)は、現在の制御システム開発で一般的であり、制御工学を学習する方法としても適している。
動的システムの時間応答を求める
動的システムの入出力関係を微分方程式で記述し、微分方程式を解くことで入力信号u(t) を入力したときの出力信号y(t) の時間的変化(時間応答)が求められる。これを微分方程式で記述した入出力関係をラプラス変換して求められた伝達関数をベースにして考える。


インパルス応答と伝達関数
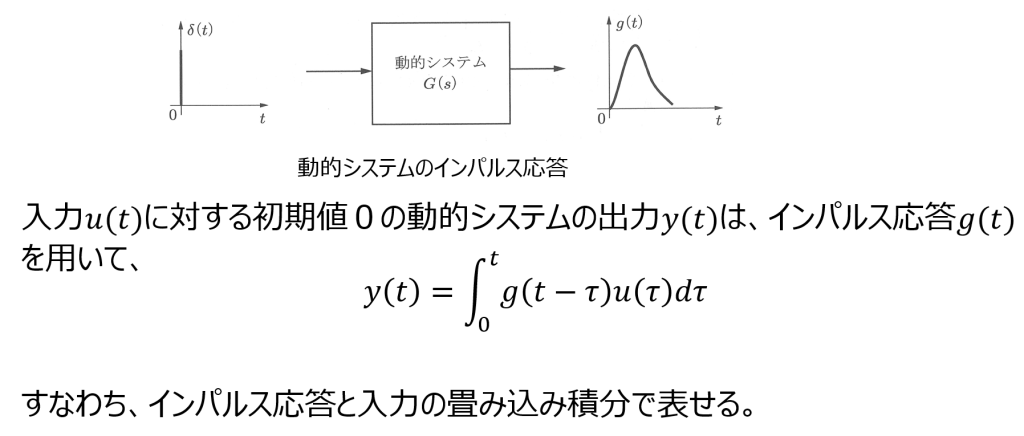
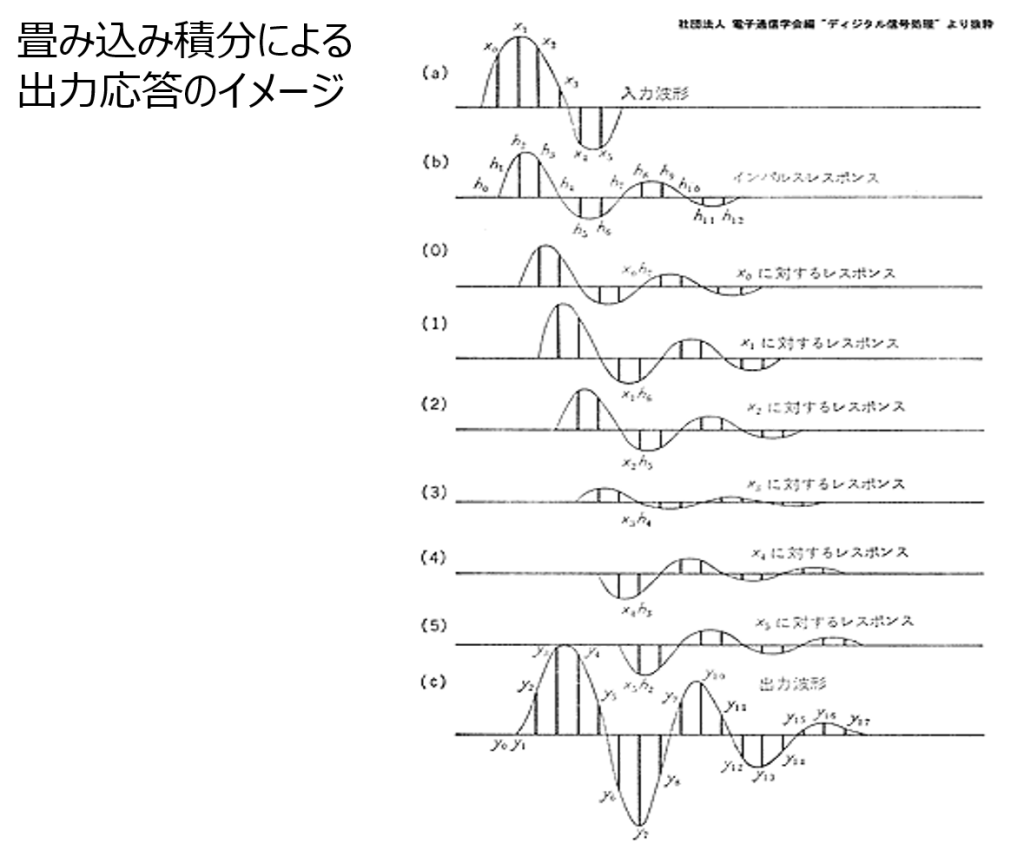
(a)を入力波形として、これはインパルス信号の集合と考えることができる。(b)をシステムのインパルス応答とすると、(a)の各インパルスに(b)の形状で応答することになる。(0)~(5)がその各インパルスに対する応答で(b)と形状が同じで振幅が(a)の各インパルスに比例する。これら(0)~(5)を足し合わせたものが出力波形(c)となる。これを厳密に連続時間において畳み込み積分で表したのが、インパルス応答が\(g(t)\)であるシステムに対して任意の入力\(u(t)\)に対する出力\(y(t)\)である。


極とインパルス応答


*極、零点の考え方は、複素関数論によっている。詳しくは、解析学の本で学んで欲しいが、概要はこちらを参考にして欲しい。



畳み込み積分のラプラス変換
畳み込み積分:$$y(t)=\int_0^t g(t-\tau) u(\tau)d\tau$$ これをラプラス変換すると、
$$Y(s)=\int_0^{\infty}\left\{\int_0^t g(t-\tau)u(\tau)d\tau \right\}e^{-st}dt$$ :積分順序を替えて
$$=\int_0^\infty \left\{\int_\tau^\infty g(t-\tau)u(\tau)e^{-st}dt\right\}d\tau$$ : \(t-\tau =x \)と変数変換する
$$=\int_0^\infty \int_0^\infty g(x)u(\tau)e^{-s(x+\tau)}dxd\tau$$
$$=\int_0^\infty g(x)e^{-sx}dx\int_0^\infty u(\tau)e^{-s\tau}d\tau$$
$$=G(s)U(s)$$
以上のように、畳み込み積分をラプラス変換すると、各関数\(g(t) , u(t)\)をラプラス変換した\(G(s) , U(s)\)の積となる。


“11. インパルス応答” に対して2件のコメントがあります。
コメントは受け付けていません。