8. 動的システム
数学によって記述されたモデルを数式モデルという。ここでモデルとは、対象とするシステムを簡略化してその性質を表したものをいう。なお、この制御工学で扱う制御対象は、機械や電気回路などの工学的な存在とする。
動的システム(Dynamic System)は、ある時間 t での出力 y がその時間の入力 u のみではなく、過去に入力してきた値や未来で入力する予定の値で決定する。従って、多くの動的システムの挙動は微分方程式で記述されることになる。
システムとは、特定の機能を有する要素が複数個相互結合したものをいう。
基礎制御工学(古典制御理論)では、要素への入力、出力に着目し、その数学モデルは、入出力関係を主に微分方程式を使って数学的に表現したものになる。
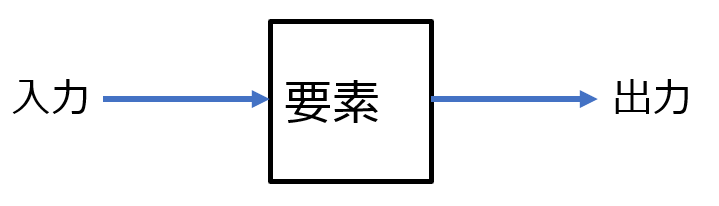
数学モデルの例(電気系の動的システム)
抵抗:オームの法則が成り立つ静的システムと見なせる要素
抵抗Rの両端に電圧 v(t) を印可すると電流 i(t) が流れる。
$$i(t)=\frac{1}{R}v(t)$$
インダクタ(コイル):インダクタ L の端子間電圧 v(t) は流れる電流i(t)の時間変化に比例する。
$$\frac{di(t)}{dt}=\frac{1}{L}v(t)$$ $$v(t)=L\frac{di(t)}{dt}$$
キャパシタ(コンデンサ):キャパシタ C の端子間電圧 v(t) は流れた電流 i(t) の時間積分(電荷)に比例する。
$$i(t)=C\frac{dv(t)}{dt}$$ $$v(t)=\frac{1}{C}\int i(t)dt=\frac{q}{C}$$
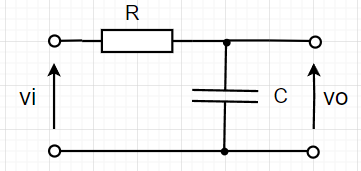
R-C回路の入出力関係
$$v_i(t)=R i(t) + v_o(t)$$ $$i(t)=C\frac{dv_o(t)}{dt} $$ $$RC\frac{dv_o(t)}{dt} + v_o(t) = v_i(t)$$
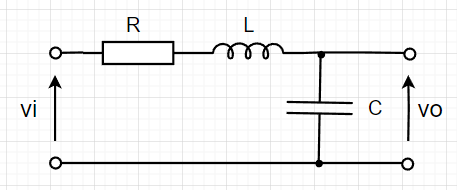
R-L-C回路の入出力関係
$$R i(t)+L\frac{di(t)}{dt} + v_o(t) = v_i(t)$$ $$i(t) = C\frac{dv_o(t)}{dt} , \frac{di(t)}{dt}=C\frac{d^2v_o(t)}{dt^2}$$ $$LC\frac{d^2v_o(t)}{dt^2} +RC\frac{dv_o(t)}{dt} +v_o(t) = v_i(t)$$

数学モデルの例(機械系の動的システム)
変位:\(x(t)\) 速度:\(v(t)\) 力:\(f(t)\) とする。
よって、 加速度: \( \frac{dv(t)}{dt}=\frac{d^2x(t)}{dt^2} \)
基本的な各機械要素は次のような数式モデルで表される。
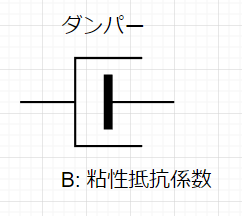
*ダンパー
$$v(t)=\frac{1}{B}f(t)$$
\(B\):粘性抵抗係数
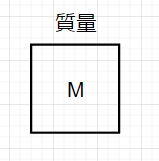
*質量
$$f(t)=M\frac{d^2x(t)}{dt^2}$$ $$\frac{dv(t)}{dt}=\frac{1}{M}f(t)$$ $$v(t)=\frac{1}{M}\int f(t)dt $$
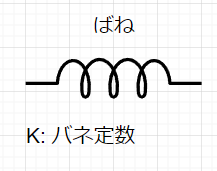
*ばね
$$f(t)=K x(t)$$ $$v(t)=\frac{1}{K}\frac{df(t)}{dt}$$

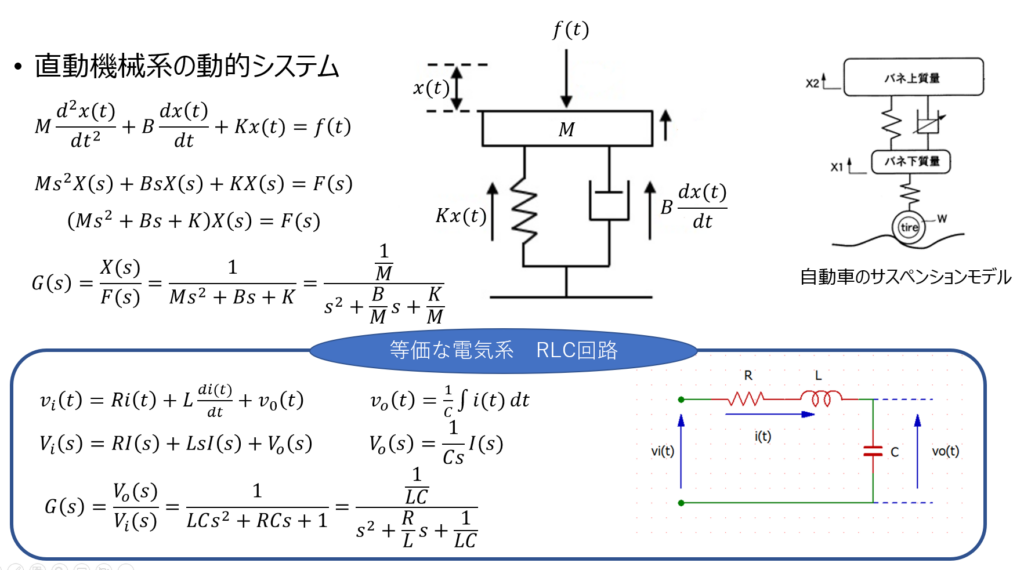
直動機械の質量、ダンパー、ばね力学系の数式モデル
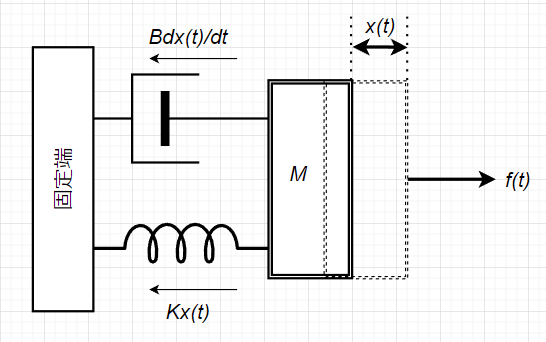
$$M\frac{d^2x(t)}{dt^2}=f(t)-B\frac{dx(t)}{dt}-Kx(t)$$ $$M\frac{d^2x(t)}{dt^2} + B\frac{dx(t)}{dt} + Kx(t)=f(t)$$


“8. 動的システム” に対して4件のコメントがあります。
コメントは受け付けていません。