16. システムの安定性

インパルス応答と伝達関数

動的システムのインパルス応答は、伝達関数の逆ラプラス変換となる。$$g(t)=\mathcal{L}^{-1}\left\{G(s)\right\}$$ 伝達関数は一般的に複素多項式の比である複素有理関数で表されるので、\(n\)次の伝達関数の分母多項式（特性方程式）\(d(s)=0\)の根（伝達関数\(G(s)\)の極）を\(p_1,p_2,\cdots,p_n\)とすると、$$G(s)=\frac{n(s)}{d(s)}$$ $$=\frac{b_ms^m+b_{m-1}s^{m-1}+\cdots+b_0}{(s-p_1)(s-p_2)\cdots(s-p_n)}$$と表せて、部分分数展開できる。すなわち、$$G(s)=\frac{A_1}{s-p_1}+\frac{A_2}{s-p_2}+\cdots+\frac{A_n}{s-p_n}$$ となる。ここで、\(A_1,A_2,\cdots,A_n\)は部分分数展開したときの係数である。これを逆ラプラス変換すると、伝達関数\(G(s)\)をもつシステムのインパルス応答が求まり、$$g(t)=\mathcal{L}^{-1}\left\{G(s)\right\}$$ $$=A_1e^{p_1t}+A_2e^{p_2t}+\cdots+A_ne{p_nt}$$となる。従って、全ての極\(p_1,p_2,\cdots,p_n\)の実部が負であれば、\(g(t)\)は十分に時間が経ったら０に収束する。極のうち一つでも実部が正だと発散することになる。(詳細な導出はこちらで）
まとめると、すべての極の実部が負（\(Re\{p\}\lt0\))ならば、このシステムのインパルス応答は十分に時間が経ったら０に収束する。

システムの安定性

安定性とは、システムの状態が何らかの原因で一時的に平衡状態または定常状態からはずれても、その原因がなくなればもとの平衡状態または定常状態に復帰するような特性をいう。これより、あるシステムのインパルス応答が十分に時間が経ったときに０に収束するということは、システムに何か信号が入ってもその信号がなくなって十分時間が経てば、応答が０になるということなのでシステムは安定といえる。もし、システムの極の一つでも負でないものがあると、インパルス応答は０に収束しないので不安定といえる。
安定条件：システムの伝達関数\(G(s)\)の全ての極の実部が負　(\(Re\{p\}\lt0\))

BIBO安定

\(y(t)=\mathcal{L}^{-1}\{G(s)U(s)\}\) （\(U(s)=\mathcal{L}\{u(t)\})\)という入出力関係を持つ因果的なシステムが、\(u(t)\) が有界なら\(y(t)\) も有界という性質を持つとき、 このシステムはBIBO安定(Bounded -Input Bounded- Output Stable)という。
BIBO安定の必要十分条件は、システムのインパルス応答を\(g(t)\)とするとき、$$\int_0^\infty\left|g(t)\right|dt\lt\infty$$ である。　また、これは1入力1出力システム（古典制御理論の範囲）の場合、インパルス応答が０に収束する$$\lim_{t\rightarrow\infty}g(t)\rightarrow0$$（漸近安定）と同等である。

極とインパルス応答

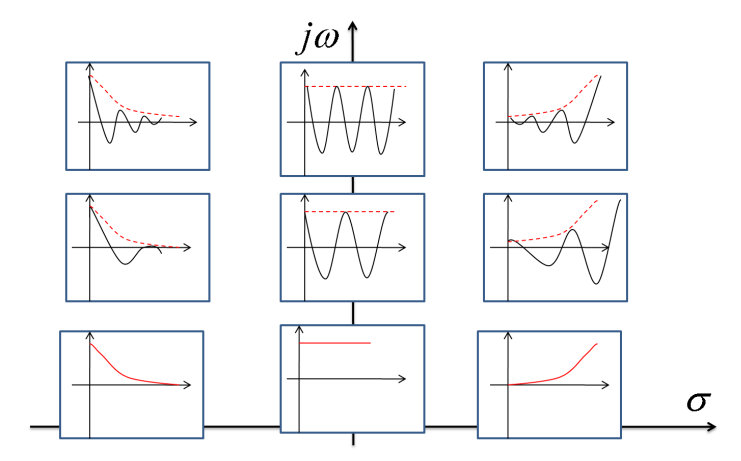
極の実部が負であればインパルス応答は０に収束する。極が負で実軸上にある場合は非振動的に減衰し０に収束する。極の実部が負の複素共役根の場合はインパルス応答は振動しながら０に収束する。極が虚軸上にある場合は定常振動となり、極が原点の場合は一定値となる。極の実部が正の場合はインパルス応答は発散する。極が正で実軸上にある場合は非振動的に発散する。極の実部が正の複素共役根の場合はインパルス応答は振動しながら発散する。