20. ベクトル軌跡とナイキスト軌跡

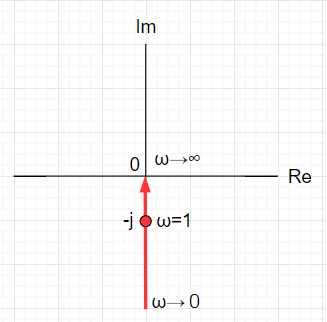
積分要素の伝達関数$G(s)=\frac{1}{s}$の周波数伝達関数は、$s \rightarrow j\omega$ として、 $$G(j\omega)=\frac{1}{j\omega}=-\frac{j}{\omega}$$ となる。従って、 $$\left|G(j\omega)\right|=\frac{1}{\omega}$$ $$\arg G(j\omega)=-90\text{°}$$ である。
$\omega \rightarrow 0$のとき、$\left|G(j\omega)\right| \rightarrow \infty$
$\omega =1$のとき、$\left|G(j\omega)\right|=1$
$\omega \rightarrow \infty$のとき、$\left|G(j\omega)\right| \rightarrow 0$
であり、位相は常に$90\text{°}$遅れである。

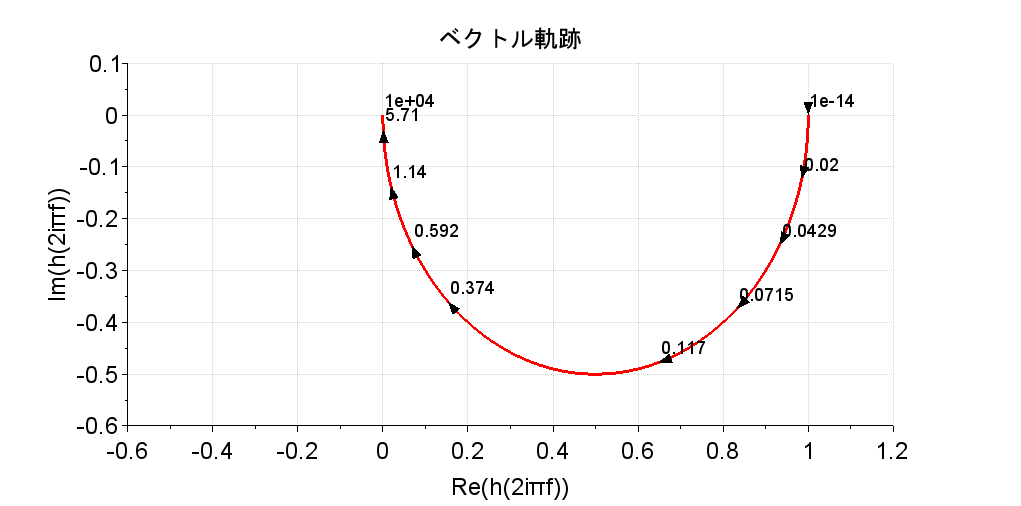
※ナイキスト軌跡は、このベクトル軌跡に実軸対称のグラフを追加した図になる。

一次遅れ系の伝達関数$G(s)=\frac{1}{1+sT}$の周波数伝達関数は、$s \rightarrow j\omega$ として、 $$G(j\omega)=\frac{1}{1+j \omega T}$$ となる。従って、 $$\left|G(j\omega)\right|=\frac{1}{\sqrt{1+(\omega T)^2}}$$ $$\arg G(j\omega)=-\tan^{-1}(\omega T)$$ である。これより、$G(j\omega)$の大きさと偏角が決定し、複素平面上にベクトルが描ける。角周波数$\omega$を$0$から$\infty$まで変化させたときのベクトルの先端の軌跡がベクトル軌跡となる。

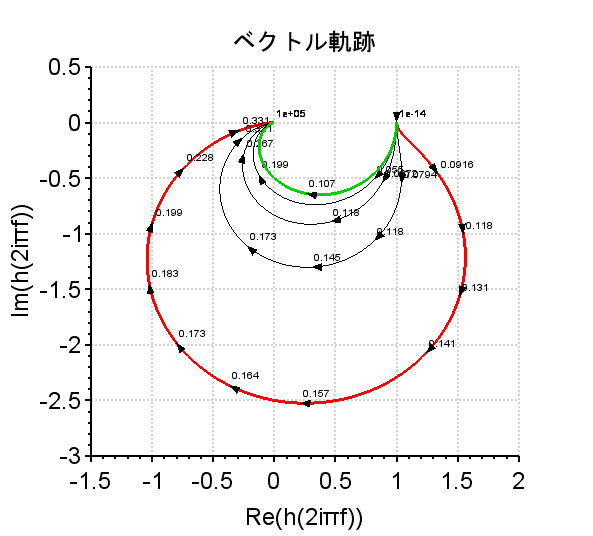
自然角周波数$\omega_n$）を１[rad/s]とし、減衰係数 $\zeta$ を0.2～1.0まで0.2刻みで変化させて、ベクトル軌跡を描いた。緑の線が$\zeta=1.0$、赤の線が$\zeta=0.2$の場合である。$\zeta$が小さいほど$\omega$に対する軌跡の変化が大きくなる。また、$\zeta > 1$の場合、一次遅れ系に近い軌跡となり、ステップ応答でも分かるように挙動も一次遅れ系に近くなる。

二次遅れ系の伝達関数は、 $$G(s)=\frac{\omega_n^2}{s^2+2\zeta \omega_n s + \omega_n^2}$$ ここで、$\omega_n$：自然角周波数、$\zeta$ ：減衰係数　である。この周波数伝達関数は、$s \rightarrow j\omega$として、 $$G(j\omega)=\frac{\omega_n^2}{-\omega^2 + j2 \zeta \omega_n \omega + \omega_n^2}$$ $$= \frac{1}{1 - \left(\frac{\omega}{\omega_n}\right)^2+j2\zeta\frac{\omega}{\omega_n}}$$ となる。従って、 $$\left|G(j\omega)\right|=\frac{1}{\sqrt{\left\{1 - \left(\frac{\omega}{\omega_n}\right)^2\right\}^2 + \left(2\zeta\frac{\omega}{\omega_n} \right)^2}}$$ $$\arg G(j\omega)=-\tan^{-1}\frac{2\zeta\frac{\omega}{\omega_n}}{1-\left(\frac{\omega}{\omega_n}\right)^2}$$ となる。

//一次遅れ系のベクトル軌跡
clear; clf();
s=%s;
//時定数　T＝１
T=1;
// 一次遅れ系の伝達関数
G=1/(T*s+1);
Gs=syslin('c',G); /* Scilab 内部のシステム表現に変換*/
//ベクトル軌跡の描画
nyquist(Gs, 0, 10000, %f);

//二次遅れ系のベクトル軌跡
clear; clf();
s=%s;
//自然角周波数 wn=1[rad/s]
wn=1;
//減衰係数 zeta (減衰係数を0.2から1.0まで変える)
for zeta=0.2:0.2:1.0
//二次遅れ系の伝達関数
G=(wn*wn)/(s^2+2.*zeta*wn*s+wn*wn);
Gs=syslin('c',G); /* Scilab 内部のシステム表現に変換*/
//ベクトル軌跡の描画
nyquist(Gs, 0, 100000, %f);
end

※nyquist()関数はsymmetry引数（グラフの対称性を指定する引数）をとれる。デフォルトでは%t（true）となっており上下対称のグラフを描くようになっている。周波数の正の範囲だけを描画させたいときはsymmetry引数を%f（false）に指定する。