23. フィードバックの安定性
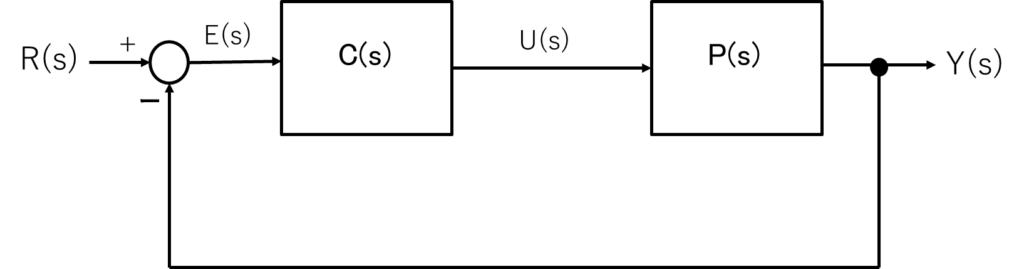
図の単位フィードバック制御系で、フィードバック制御系の安定性について考える。
システムの安定条件は、伝達関数の全ての極が複素平面の左半平面にあることである。
フィードバック制御系では、入力から出力までの伝達関数(閉ループ伝達関数T(s))は、開ループ伝達関数L(s)=P(s)C(s)とすると、T(s)=\frac{L(s)}{1+L(s)}=\frac{P(s)C(s)}{1+P(s)C(s)}で表せる。
従って、T(s)の極は、1+L(s)=0の根となる。1+L(s)=0を特性方程式と呼び、その根を特性根と呼ぶ。この特性根は、閉ループ伝達関数T(s)の極となる。これより、全ての特性根(すなわち閉ループ伝達関数の極)がRe\{p_i \} \lt 0 (極の実部が負)であればフィードバック制御系は安定といえる。
特性方程式:1+L(s)=0 で、開ループ伝達関数L(s)は、L(s)=\frac{q(s)}{p(s)} q(s)=K(s - z_1)(s - z_2) \cdots (s - z_m) p(s)=(s - p_1)(s - p_2) \cdots (s - p_n)と表せ、閉ループ伝達関数T(s)は、T(s)=\frac{L(s)}{1+L(s)}=\frac{\frac{q(s)}{p(s)}}{1+\frac{q(s)}{p(s)}}=\frac{q(s)}{q(s)+p(s)}と表せる。従って、閉ループ伝達関数T(s)の分母多項式は、d(s)=q(s)+p(s) =K(s - z_1)(s - z_2) \cdots (s - z_m) + (s - p_1)(s - p_2) \cdots (s - p_n) となる。閉ループ伝達関数T(s)の全ての特性根(極)が複素平面の左半平面にあれば安定なので、特性方程式d(s)=0(sの高次方程式)にラウス・フルビッツの安定判別法を適用すれば、閉ループ伝達関数の安定性が分かる。(安定性の判別だけであれば、特性方程式の根の実部の正負が分かれば良いということになるので、ラウス・フルビッツの安定判別法の適用で良い。)
フィードバック制御系の安定判別の例
制御対象がP(s)=\frac{1}{2s-1}(不安定な制御対象)で、制御器をC(s)=\frac{3}{s+1}として、単位フィードバック制御系を構成する。このときの制御系の安定性を考える。
開ループ伝達関数は、L(s)=P(s)C(s)=\frac{1}{2s-1} \cdot \frac{3}{s+1} =\frac{3}{(2s-1)(s+1)}=\frac{q(s)}{p(s)}となる。閉ループ伝達関数は、T(s)=\frac{L(s)}{1+L(s)}となるので、特性方程式は、1+L(s)=1+\frac{q(s)}{p(s)}=\frac{q(s)+p(s)}{p(s)} =\frac{d(s)}{p(s)}=0となる。整理すると特性方程式は、d(s)=q(s)+p(s)=3+(2s-1)(s+1) =2s^2+s+2=0となる。この根(特性根)は、\frac{-1\pm j\sqrt{15}}{4}と求まる。特性根の実部(-\frac{1}{4})が負なので、この制御系は安定である。
ナイキストの安定判別法
特性方程式より、1+L(s)=\frac{q(s)+p(s)}{p(s)} =\frac{(s - l_1)(s - l_2) \cdots (s - l_n)}{(s - p_1)(s - p_2) \cdots (s - p_n)}=0 つまり、特性方程式1+L(s)=0の全ての零点{l_1, l_2, \cdots , l_n}が複素平面の左半平面にあれば安定ということになる。(閉ループ伝達関数の全ての極が左半平面にあれば安定ということ)
このことより、開ループ伝達関数L(s)=\frac{q(s)}{p(s)}より、p(s)+q(s)(つまり、開ループ伝達関数L(s)の分母多項式と分子多項式)で安定判別が可能といえる。
ナイキストの安定判別法(1)
L(s)の不安定極の数をp個とする。 s \rightarrow j\omegaとおいて、\omega = -\infty \sim +\infty として、L(j\omega)の描くナイキスト軌跡がn回 L(s)平面上の点(-1,j0 )を反時計方向に回るとする。このとき、z=p-n=0 が成立すればフィードバック制御系は安定である。
※詳細を追記予定。
ナイキストの安定判別法(2)
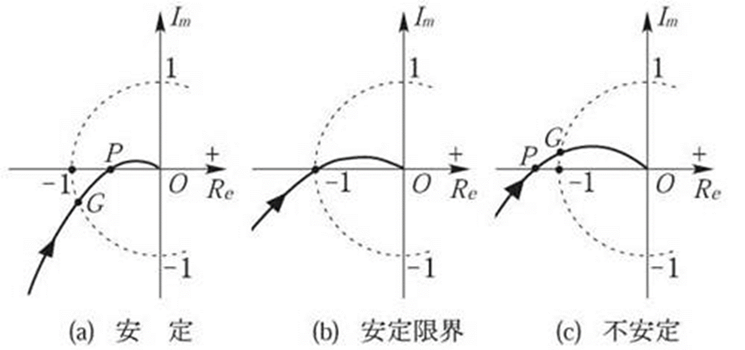
実際の制御系では、L(s)が不安定極を持たない場合が多い。この場合p=0なので、ナイキストの安定判別は簡単になる。
s \rightarrow j\omegaとおいて、\omega = 0 \sim +\infty としてL(j\omega)の描くベクトル軌跡が、
複素平面上の
点(-1,j0)を左側に見れば安定、
点(-1,j0)を右側に見れば不安定、
点(-1 ,j0)上を通れば安定限界といえる。
ナイキストの安定判別法の例
制御対象P(s)=\frac{1}{2s-1}(不安定な制御対象)で、制御器をC(s)=\frac{3}{s+1}とする。L(s)=P(s)C(s)=\frac{3}{(2s-1)(s+1)} =\frac{3}{2s^2+s-1} L(j\omega)=\frac{3}{-(\omega ^2 +1)+j\omega} よって、大きさ(利得):\left|L(j\omega)\right| = \frac{3}{\sqrt{(\omega ^2+1)^2 + \omega ^2}} 位相:\arg \{L(j \omega)\} = \tan^{-1} \left(\frac{\omega}{\omega ^2 +1}\right)
Scilabのスクリプト
//ナイキストの安定判別法(2)を適用した例
clear; clf;
s=%s;
P=1/(2*s-1);
Ps=syslin('c',P);
//C(s)を使わない場合 (C(s)が1)
scf(0);
nyquist(Ps,%f);
//C(s)を使う場合
C=3/(s+1);
L=P*C;
Ls=syslin('c',L);
scf(1);
nyquist(Ls,%f);
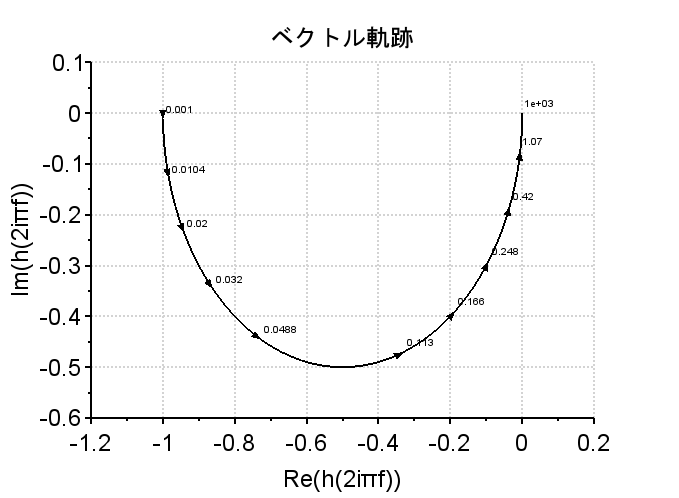
C(s)を使わない場合、すなわちP(s)だけでフィードバック制御系を構成した場合、L(j\omega)=P(j\omega)のベクトル軌跡は、点(-1 ,j0)上を通るので安定限界(一般的には不安定といえる)となる。
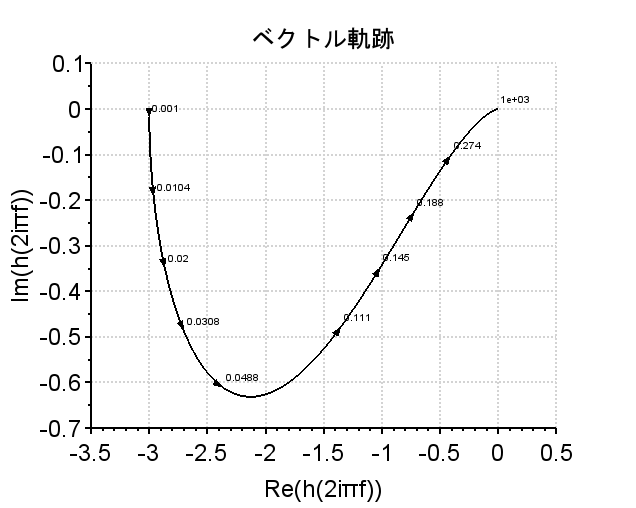
C(s)を使ってフィードバック制御系を構成した場合は、L(j\omega)=P(j\omega)C(j\omega)のベクトル軌跡は、\omega = 0 \sim +\infty としたとき、点(-1 ,j0)を左側に見るので安定となる。
フィードバック制御による安定化の例
制御対象をP(s)=\frac{1}{3s-6}とする。このとき、特性方程式は3s-6=0なので極は2となり複素平面の右半平面に極があるので不安定な制御対象とわかる。インパルス応答を求めると、g(t)=\mathcal{L}^{-1}\left\{\frac{1}{3s-6}\right\} =\mathcal{L}^{-1}\left\{\frac{\frac{1}{3}}{s-2}\right\} =\frac{1}{3}e^{2t}となり、t \rightarrow \inftyで発散する。このことからも制御対象P(s)が不安定であることがわかる。
制御器をC(s)=K(ゲイン制御)として、フィードバック制御を構成すると閉ループ伝達関数は、T(s)=\frac{KP(s)}{1+KP(s)}=\frac{\frac{K}{3s-6}}{1+\frac{K}{3s-6}} =\frac{K}{3s-6+K}となる。このとき特性方程式は、3s-6+K=0になるので、特性根(閉ループ伝達関数の極)が負になるためには、K \gt 6が安定条件となる。
例えば、C(s)=K=10とするとT(s)=\frac{10}{3s+4}=\frac{10}{3}\cdot \frac{1}{s+\frac{4}{3}}となり、インパルス応答はg(t)=\mathcal{L}^{-1}\left\{T(s)\right\}=\frac{10}{3}e^{-\frac{4}{3} t}となり、制御系が安定となることがわかる。
しかし、単位ステップ応答はy(t)=\mathcal{L}^{-1}\left\{\frac{10}{3s+4} \cdot \frac{1}{s}\right\}=\frac{5}{2}-\frac{5}{2}e^{-\frac{4}{3} t} となり、y(\infty )=\frac{5}{2}となる。つまり、単位ステップ 1 に一致しない、定常偏差が生じることになる。よって、C(s)=K(ゲイン制御)では安定化できても制御器としては不十分ということになる。


“23. フィードバックの安定性” に対して2件のコメントがあります。
コメントは受け付けていません。