28. 補償器の設計

線形制御理論の範囲での制御器（補償器）設計の概要

古典制御理論（classical control theory）では、一入力一出力（SISO）システムを主に扱い、周波数応答による制御器設計を考え、最適化やモデル化誤差の影響抑制は経験と試行錯誤で補うことが多い。近年（といっても20年以上は経つが）では、コンピュータシミュレーションが発達したので、周波数応答法で設計し、時間応答の結果で制御器を修正するなどの手法をとることも多い。古典といっても現代でもPID制御などは産業での主力の制御手法として使われている。

現代制御理論（modern control theory） では、時間領域における最適化設計を主に考える。精密な数理モデルに基づく最適化設計で、状態フィードバック、状態観測器、最適制御などの設計手法を使う。多入力多出力（MIMO）システムも統一的に扱える。しかし、モデル化誤差などは反映できないため、周波数応答などを使いながら制御器の調整が必要になる。

ロバスト制御理論（\(H^\infty\)制御など）では、周波数応答を含んだ制御器の最適化設計手法となっており、モデル化誤差を許容する制御器の最適化設計ができる。線形制御理論の範囲では、古典制御理論、現代制御理論を統合した制御器設計手法といえる。

※補償器（compensater）：制御対象単独でフィードバックしても望む特性が得られず、制御対象と直列に挿入するか、フィードバックループに入れ、閉ループの特性を望ましい設計仕様に修正/補償することから補償器という。制御器の一形態だが、古典制御理論の範囲では、制御器と補償器は同じと考えて問題ない。電気電子回路での補償器は少し意味が異なってくる。

周波数応答による制御器設計の基本（古典制御理論）

フィードバック制御系に適切な制御器を挿入することにより、安定化、目標値追従性能の改善、外乱抑制、パラメータ変動の影響抑制などを実現する。制御系設計の手順は、以下のようになる。
１．制御対象のモデル化（システム同定）
２．制御対象の解析（解析、シミュレーション）
３．制御系の仕様の作成（制御要求の分析に基づき制御仕様を決定）
４．制御器の設計
５．性能評価（シミュレーション、実機実装実験）仕様を満たさない場合は手順３に戻る。
＊場合によっては、１．制御対象のモデル化に戻る。

開ループ伝達関数\(L(s)\)を基にした周波数応答による補償器の設計

時間応答のパラメータ値（\(t_r,t_d, A_p\)など）と補償器の伝達関数\(C(s)\)との明確な関係を見つけるのは困難である。そのため、以下の設計仕様を基に設計することが多い。
＊閉ループ伝達関数の周波数応答による仕様
・\(M_p\)は\(1.1 \sim 1.5\)にする。\(\omega_b\) は立ち上がり時間を満たすように適切にとる。（\(\omega_b\)はなるべく高く）
・定常特性として、位置偏差、速度偏差、加速度偏差を適切な値にとる。
閉ループ伝達関数は、\(T(s)=\frac{C(s)P(s)}{1 + C(s)P(s)}\)  であり、制御器\(C(s)\)が分母、分子にあり、制御器設計の見通しが難しい。\(L(s)=C(s)P(s)\) に置き換えると、\(T(s)=\frac{L(s)}{1 + L(s)}\) となる。従って、\(L(s)\)を基に制御器\(C(s)\)の設計を考えると制御器設計の見通しが良くなる。
＊開ループ伝達関数の周波数応答による仕様（\(T(s) \rightarrow L(s)\)）
・ゲイン余裕 \(g_m\)を\(10 \sim 20\)dB、位相余裕 \(p_m\) を\(40^{°} \sim 60^{°}\)程度とし、ゲイン交差周波数 \(\omega_c\) はバンド幅\(\omega_b\) を満たす様に十分に高くとる。
・定常偏差か定常偏差定数の値、あるいは開ループ伝達関数\( L(s)\) の型を指定する。

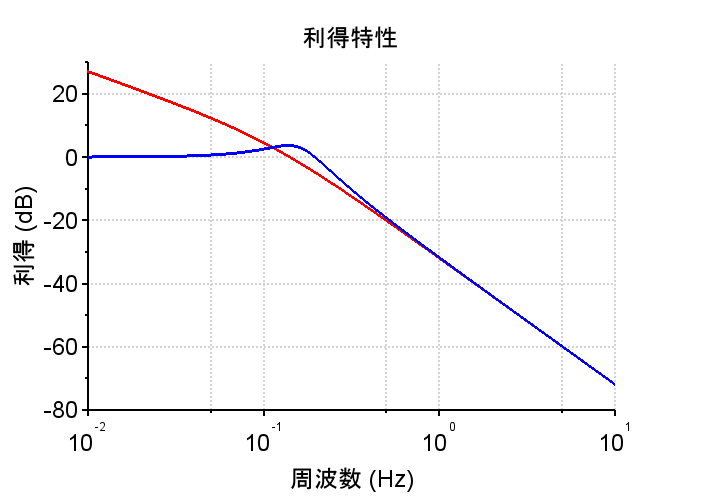
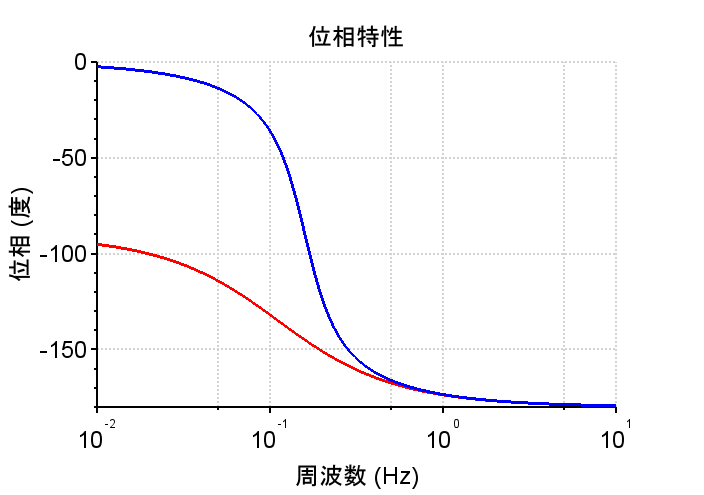
\(L(s)\)と\(T(s)\)の例（Scilabスクリプト）

\(L(s)\)と\(T(s)\)のボード線図の関係から、開ループ伝達関数の周波数応答による仕様をもとに制御器を設計するとよいことが分かる。
\(T(s)=\frac{L(s)}{1 + L(s)}\)の関係にあるので、\(L(s)\)の利得が高い低域では、\(T(s)\)は\(0\)ｄBとなり、位相は\(0^{°}\)となる。\(T(s)\)がこの特性を示す範囲では、目標値に出力が一致することになる。
※ボード線図を描く場合は、\(s \rightarrow j\omega \)としている。

//開ループL(s)と閉ループT(s)の周波数応答特性
clear; clf();
s=%s;

L=1/(s*(s+0.7)); /*開ループ伝達関数*/
T=L/(1+L); /*閉ループ伝達関数*/
Ls=syslin('c',L);
Ts=syslin('c',T);

//ボード線図
scf(0);
gainplot([Ls;Ts],0.01,100);
scf(1);
phaseplot([Ls;Ts],0.01,100);