29. ゲイン補償器
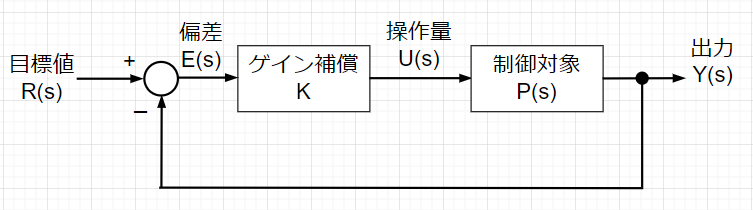
開ループ伝達関数\(L(s)\)をもとにした制御器の設計例を考える。まず、もっとも単純な制御器であるゲイン補償器だけでの特性調整を検討する。
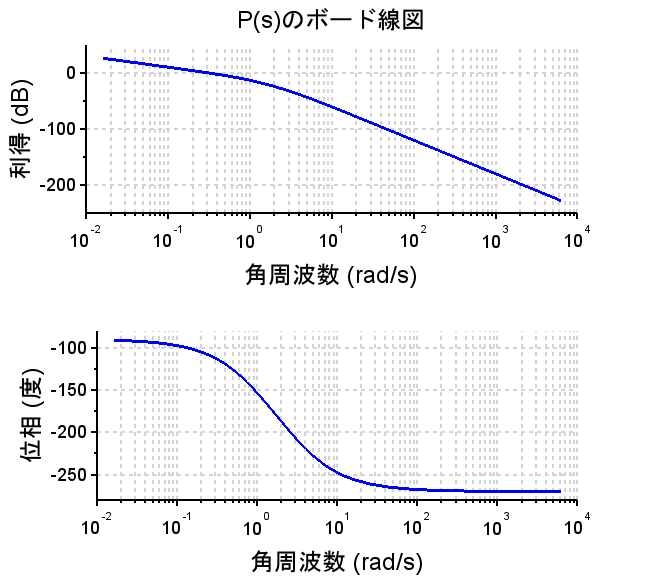
制御対象を$$P(s)=\frac{1}{s(s+1)(s+3)}$$とする。\(P(s)\)の極は、\([0, -1, -3]\)なので安定限界(不安定)である。また、\(\frac{1}{s}\)を持っているので1型系である。この制御対象の伝達関数\(P(s)\)は、電動モータなどの伝達関数を単純化したものである。
制御仕様は以下とする。
・位相余裕\(p_m=45^{°}\)程度、ゲイン余裕\(g_m=12dB\)程度、ゲイン交差周波数\(\omega_c\)はできるだけ高くとる。
・定常位置偏差\(e_p=0\)、定常速度偏差\(e_v=0.5\)を目標とする。
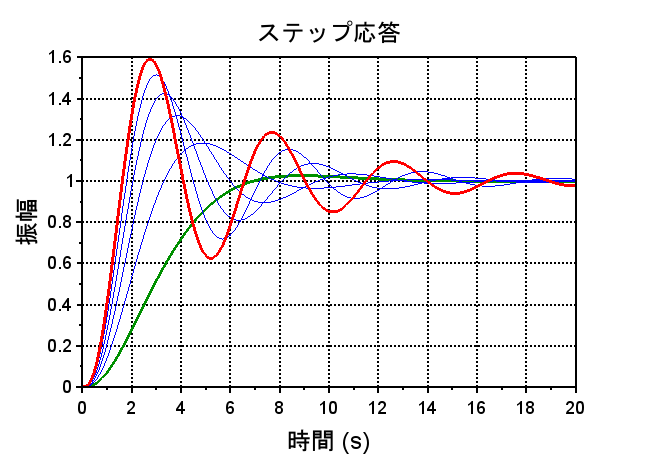
\(K=1\):緑線、\(K=6\):赤線
ゲイン補償は、\(L(s)\)の利得調整だけで制御系の特性を改善する 手法である。制御対象が\(P(s)=\frac{1}{s(s+1)(s+3)}\)で、 補償器は\(C(s)=K\)なので、開ループ伝達関数は、$$L(s)=C(s)P(s)=\frac{K}{s(s+1)(s+3)}$$であり、閉ループ伝達関数は、$$T(s)=\frac{L(s)}{1 + L(s)}=\frac{K}{s(s+1)(s+3)+K}$$である。特性方程式は、$$1 + L(s)=s(s+1)(s+3)+K$$ $$=s^3+4s^2+3s+K=0$$である。ラウスの安定判別から、\(0 \lt K \lt 12\) と制御系を安定にする\(K\)の範囲が分かる。
開ループ伝達関数が\(L(s)=C(s)P(s)=\frac{K}{s(s+1)(s+3)}\)と1型系なので、内部モデル原理より定常位置偏差\(e_p=0\)である。
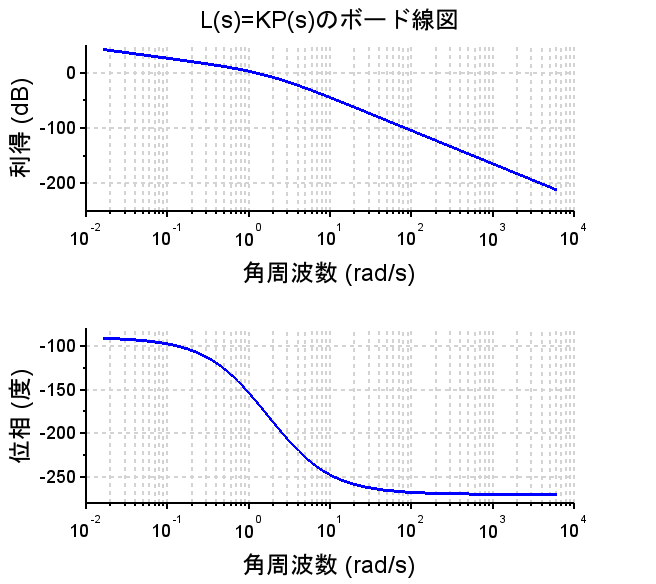
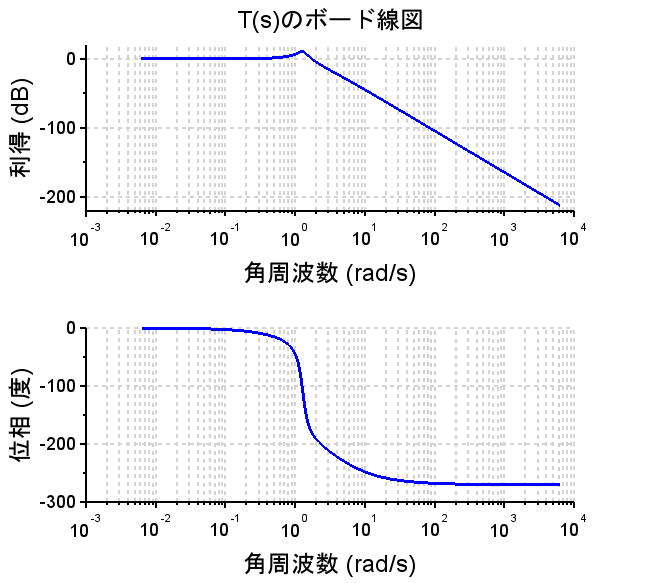
制御仕様の定常速度偏差\(e_v=0.5\)を満たすには、\(e_v=\frac{1}{K_v}=0.5\) \(K_v=2\) $$Kv=\lim_{s \rightarrow 0} sL(s)=\lim_{s \rightarrow 0}\frac{K}{(s+1)(s+3)}$$ $$=\frac{K}{3}=2$$ よって、\(K=6\)となる。以上より、開ループ伝達関数は、$$L(s)=\frac{6}{s(s+1)(s+3)}$$閉ループ伝達関数は、 $$T(s)=\frac{6}{s(s+1)(s+3)+6}$$となる。しかし、このゲイン補償では\(L(s)=KP(s)\)のボード線図からわかるように、制御仕様の位相余裕\(p_m=45^{°}\)程度、ゲイン余裕\(g_m=12dB\)程度を満たすことができない。ステップ応答から分かるようにゲイン\(K=6\)(赤線)にすると行き過ぎ量が大きくなり安定性が悪くなる。
制御仕様を満たすにはゲインを下げる必要があるが、ゲインを下げると定常速度偏差\(e_v=0.5\)の仕様を満たすことができない。以上よりゲイン補償だけでは、制御仕様を満たせないことになる。
ゲイン補償(Scilabスクリプト)
//ゲイン補償器
clear; clf();
s=%s;
//制御対象P(s)の周波数応答
P=1/(s*(s+1)*(s+3));
Ps=syslin('c',P);
scf(0);
bode(Ps,'rad');
//ゲイン補償
K=6;
L=K*P;
Ls=syslin('c',L);
scf(1);
//ゲイン補償したときのL(s)周波数応答
bode(Ls,'rad');
scf(2);
//ゲイン補償したときのT(s)周波数応答
T=(K*P)/(1+K*P);
Ts=syslin('c',T);
bode(Ts,'rad');
scf(3);
//Kを変化させたときのステップ応答変化
for K=1:1:6
T1=(K*P)/(1+K*P);
T1s=syslin('c',T1);
t=0:0.1:20;
y1=csim('step',t,T1s) ;
plot(t,y1);xgrid;
end;


“29. ゲイン補償器” に対して2件のコメントがあります。
コメントは受け付けていません。