32. 積分補償器

積分補償器（PI制御器）は、主に低域の利得を上げることで、定常偏差を低減させることに使われる。積分補償器の伝達関数は、$$C(s)=\frac{1 + Ts}{s}$$である。周波数伝達関数は、$$C(j\omega)=\frac{1 + j\omega T}{j \omega}$$利得は、$$\left|C(j \omega) \right | = \frac{\sqrt{1 + (\omega T)^2}}{\omega}$$ となり、\(\omega \rightarrow 0\)で、\(\left|C(j \omega)\right| \rightarrow \infty\)となる。また、\(\omega \rightarrow \infty\)で、\(\left|C(j \omega)\right| \rightarrow 1 (=0dB)\)となる。位相は、$$\phi(\omega) = \tan^{-1} \omega T - 90^{°}$$なので、低域での位相は\(- 90^{°}\)で高域での位相は\(0^{°}\)となる。
積分補償器の働きは、
・定常特性の改善
・低周波領域における外乱抑圧特性の改善
である。

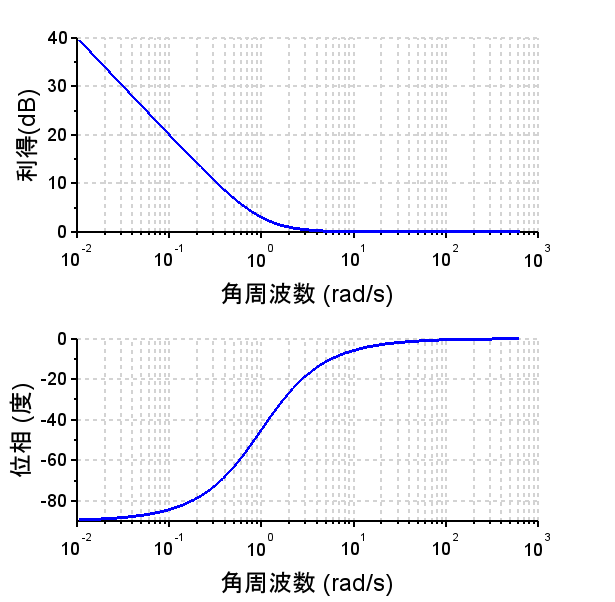
積分補償器の例
（Scilabスクリプト）

\(T = 1\)とすると、\(C(s) = \frac{1 + s}{s}\)で、周波数伝達関数は、$$C(j \omega) = \frac{1 + j \omega}{j \omega}$$で、利得は、$$\left|C(j \omega) \right| = \frac{\sqrt{1 + \omega^2}}{\omega}$$位相は、$$\phi(\omega) = \tan^{-1}\omega - 90^{°}$$である。

//積分補償器
clear; clf();
s=%s;
//T=1
T=1;
C=(1+T*s)/s;
Cs=syslin('c',C);
scf(0);
bode(Cs,10^-4,10^2,'rad');