34. 根軌跡法
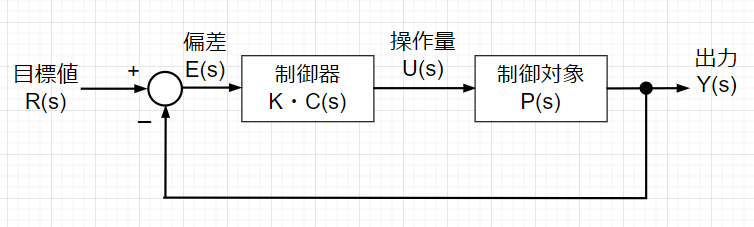
制御対象\(P(s)\)、直列制御器\(C(s)\)とした単位フィードバック制御系を考える。開ループ伝達関数は\(L(s) = C(s)P(s)\)であり、制御器\(C(s)\)の前にゲイン\(K\)を入れると\(L(s)=KC(s)P(s)\)となる。この時、閉ループ伝達関数は、$$T(s)=\frac{KC(s)P(s)}{1 + KC(s)P(s)}$$となる。従って、特性方程式は、$$1+KC(s)P(s)=0$$となるので、特性根はゲイン\(K\)によって変化する。\(K\)を\(0 \sim \infty \)まで変化させると、特性根も変化する。\(K\)に応じたこの特性根の変化を複素平面上のグラフにしたものが根軌跡であり、この根軌跡から制御系を安定にする\(K\)の範囲を求める。
根軌跡法では、変化させることができるパラメータはゲイン\(K\)だけなので、制御系全体の構成、例えば、位相進み補償器などを決定した後に、ゲイン調整する際に使うのが適している。
根軌跡の例
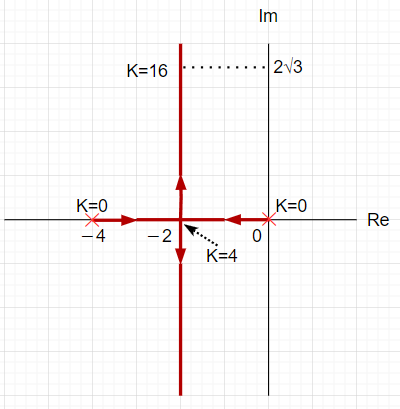
\(L(s)=C(s)P(s)=\frac{1}{s(s+4)}\)にゲイン補償\(K\)を直列に入れる。この時、閉ループ伝達関数は、$$T(s)=\frac{KL(s)}{1 + KL(s)}=\frac{K}{s(s+4)+K}$$となる。特性方程式は、$$s(s+4)+K=s^2+4s+K=0$$なので、特性根( \(T(s)\)の極 )は、$$p = -2 \pm \sqrt{4 - K}$$である。\(K \lt 0 \)のとき、特性根の実部が正となるため制御系は不安定となる。
根軌跡(\(K \ge 0\)による根の変化)は、\(K=0\)の時の根\([0, -4]\)から根\(-2\) (重根)に向かって変化して、そこから\(p=-2 \pm j\sqrt{K - 4}\) (共役複素根)の2方向に分岐していく。この例の場合、\(K\)が大きくなっても安定であるが、根の虚部が大きくなるので、時間応答特性では振動が大きくなる。
| \(K\)の範囲 | 根の値 |
| \(K=0\) | \(p=0, -4\) |
| \(K \lt 4\) | \(p=-2 \pm \sqrt{4 - K}\) (2実根) |
| \(K=4\) | \(p=-2\)(重根) |
| \(K \gt 4\) | \(p=-2 \pm j\sqrt{K - 4}\) (共役複素根) |
根軌跡の性質
特性方程式は、$$1 + L(s) =0 ,\enspace \enspace L(s)=KC(s)P(s)$$で、$$L(s)=\frac{K(s-z_1)(s-z_2) \cdots (s-z_m)}{(s-p_1)(s-p_2) \cdots (s-p_n)}$$ $$(n \ge m)$$なので、$$(s-p_1)(s-p_2) \cdots (s-p_n)$$ $$+ K(s-z_1)(s-z_2) \cdots (s-z_m) = 0$$となる。\(K\)を\(0 \sim \infty\)まで変化させ、根を求めて複素平面上に描画する。
・根軌跡は実軸に対して対称。(代数方程式の複素数の根は共役複素数となるから)
・根軌跡は\(n\)本の枝からなる。各枝は、\(L(s)\)の極\({p_1,p_2, \cdots ,p_n}\)より出発し、\(m\)本は零点\({z_1,z_2, \cdots ,z_m}\)に終わり、残りの\((n-m)\)本は無限遠点に向かう。
(詳細を追記予定です。)
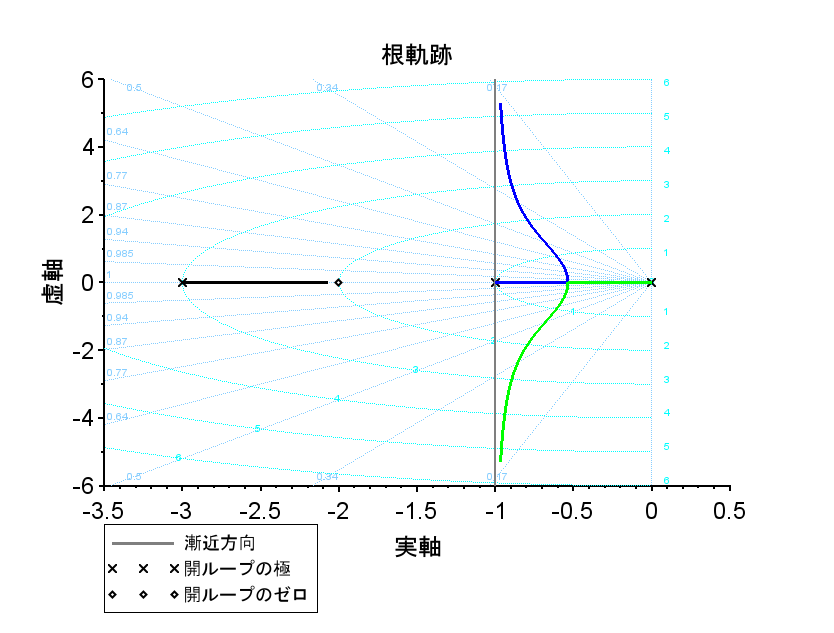
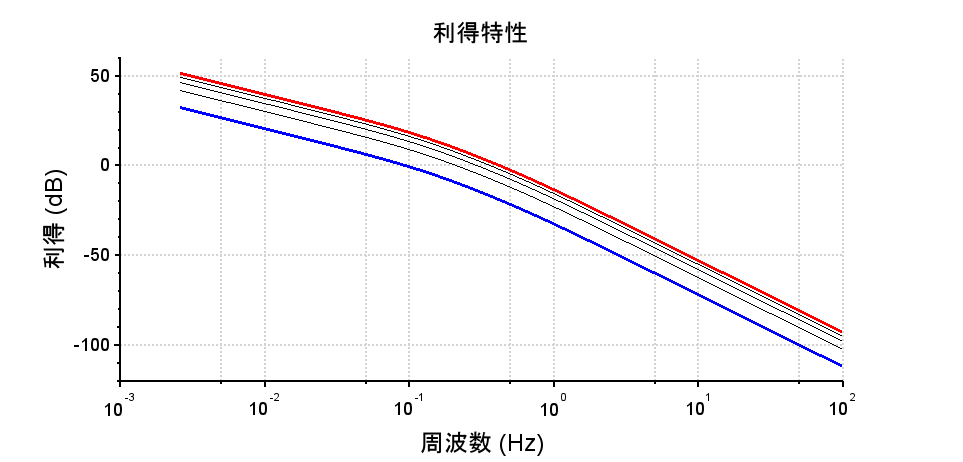
根軌跡(Scilabスクリプト)
開ループ伝達関数\(L(s)\)は、$$L(s)=\frac{s+2}{s(s+1)(s+3)}$$なので、極は\({0, -1, -3}\)で、零点は、\({-2}\)で、根軌跡は\({0, -1, -3}\)より出発し、1本は\({-2}\)に終わり(黒の線)、2本は無限遠点に向かう(青と緑の線)。
//根軌跡法
clear;clf();
s=%s;
//開ループ伝達関数
L=(s+2)/(s*(s+1)*(s+3));
Ls=syslin('c',L);
scf(0);
//根軌跡
evans(Ls,30);sgrid(); /*30は最大ゲイン*/
for K=1.0:2.0:9
L2=K*L;
L2s=syslin('c',L2);
scf(1);
gainplot(L2s,10^-3,10^2); /*利得線図*/
scf(2);
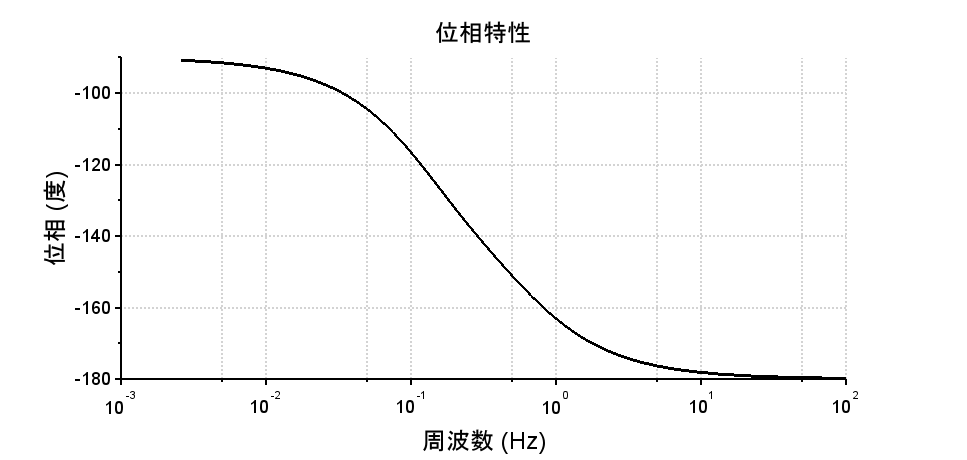
phaseplot(L2s,10^-3,10^2); /*位相線図*/
T=L2/(1+L2); /*閉ループ伝達関数*/
Ts=syslin('c',T);
t=0:0.1:10;
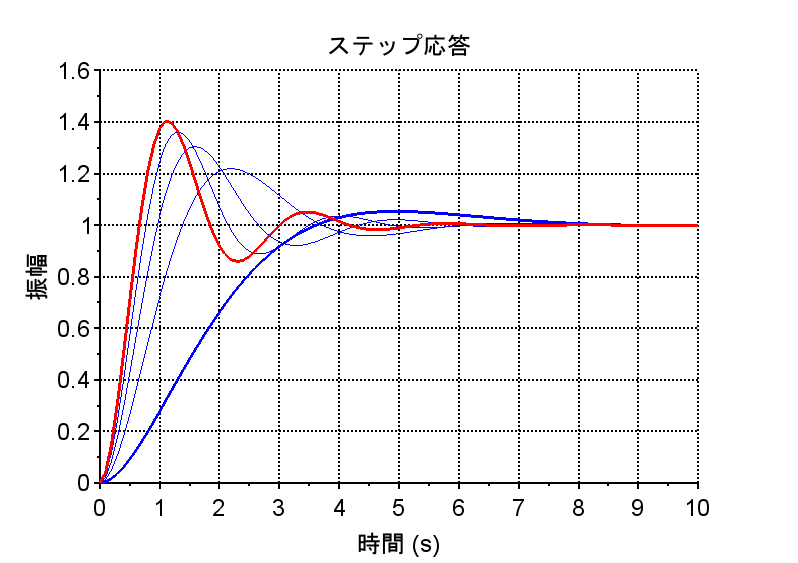
y=csim('step',t,Ts); /*ステップ応答*/
scf(3);
plot2d(t,y,2);xgrid;
end

