36. PID調節計の事例

調節計では、温度・湿度・圧力・流量等のプロセス量（測定値）を目標値（設定値）に一致させるように、内蔵のMCUにより演算して制御する。表示部に測定値と設定値を示す機器構成が多い。
機器に組み込み制御システムとして構築する場合は、プロセス量を入力するセンサとヒータなどの負荷を制御する操作器をこの調節計に接続することになる。

PID制御に関する基本用語

PID調節計による温度制御

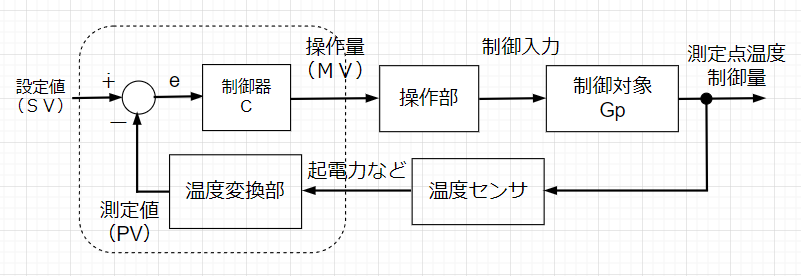
温度制御の場合、設定値温度（SV）と測定点温度（制御量）が等しくなるように操作量（MV）を与える。操作量（MV）は操作部で電圧などの制御入力に変換され制御対象Gpに加えられる。偏差eは、設定値（SV）と測定値（PV）の差である。測定値（PV）は、測定点温度（制御量）を温度センサで検出し、温度変換部でディジタル値に変換した値である。また、図の破線部が温度調節計の機能に相当するブロック線図で、制御器CがPID制御の機能を有する部分である。

PID制御の計算式と動作

PID制御の基本式は、偏差\((e=SV-PV)\)に比例するP動作（比例動作）と、偏差\(e(t)\)の積分に比例するI 動作（積分動作）、偏差\(e(t)\)の微分に比例するD動作（微分動作）の和で表す。
$$MV = K_p\left (e(t) + \frac{1}{T_i}\int e(t) dt + T_d \frac{de(t)}{dt}\right )$$
式 の右辺の第1項から順番にP動作出力、I 動作出力、D動作出力を示してる。
\(MV\)：操作量［%］、　\(e\)：偏差\(=SV-PV\) [℃］、　\(K_p\)：比例ゲイン［%／℃］、
\(T_i\)：積分時間［s］、　\(T_d\)：微分時間［s］
\(K_p = \frac{100}{PB}\)として、比例帯\(PB\)［℃］を設定することも多い。
基本的に設定可能なパラメータは比例ゲイン\(K_p\)、積分時間\(T_i\)、微分時間\(T_d\)の３つである。
以下、各動作について説明する。

P動作出力\(u_p\)は、現在の偏差\(e\)に比例した出力を出す。$$u_p=K_p \cdot e=\frac{e}{PB}\cdot 100 [\text {%} ]$$比例ゲイン\(K_p\)を大きくすることで、偏差\(e\)に応じたP動作出力が大きくなる。ただし、実際の操作量\(MV\)は\(0 \sim 100 [\text{%}]\)なので、その範囲の値しか出力されない。つまり上限、下限でリミッターがかかることになる。また、偏差\(e(t)\)が\(0\)のとき、Ｐ動作出力は\(0 [\text{%}]\) となる。このため、Ｐ動作だけではオフセットが必ず発生する。オフセットを除去するためには、負荷特性に合わせて手動でリセット値（オフセットを見越した操作量）を加えるか、I 動作を入れる必要がある。（現実的にはI 動作を入れるのが妥当である。）

基礎的な理論と異なり、実践では操作量\(MV\)の範囲は、図のように上限、下限で制限される。上下限の操作量が制限されることで、制御系は比例範囲外で非線形動作となる。そのため、多くの場合で時間応答特性は劣化する。
この場合、詳細な動作は非線形制御理論による解析が必要となる。
手っ取り早い実践的な設計・解析手法としては、線形領域の範囲で設計してパラメータを設定した後、時間領域でのシミュレーション（MATLABのSimulinkやScilabのXcos）でリミッター要素を入れて非線形範囲での動作の概略を把握して、パラメータを再調整する手段が考えられる。（Xcosに関しては別項目で紹介する。）

PI動作出力　\(u_i\)

P動作が基本であり、これにI（積分）動作出力を加える。$$u_i = K_p \left( e(t) + \frac{1}{T_i}\int e(t) dt\right )$$I 動作は過去の偏差\(e(t)\)を積算した値であるため、\(e(t) \gt 0 \)であれば次第に増加し、\(e(t) \lt 0\)であれば次第に減少することになる。P動作が偏差に比例した一定の出力を出すのに対して、I 動作は偏差\(e(t)\)が\(0\)でない限り出力を増加（または減少）し続ける。このため、積分時間\(T_i\)によって収束速度に違いはあってもいつかはオフセットが\(0\)になる。ここで大事なのは、偏差\(e(t)\)が\(0\)になったとしても、それまでの積分値は保持されるので、手動で入れるリセット値を自動修正したのと同じような効果を得ることができる。

PD動作出力　\(u_d\)

P動作に偏差\(e(t)\)の微分に比例するD動作出力を加えると、PD動作となる。$$u_d = K_p \left(e(t) + T_d\frac{de(t)}{dt} \right)$$D動作は偏差\(e(t)\)の微分値に比例した出力を与え、未来における偏差の変化速度を抑制する。D動作は変化速度の方向に対して逆向きの抵抗力を発生させるので、ダンパー（制振器）に例えることができる。\(PV = SV\)で安定していた温度が外乱などにより急降下した場合\(\frac{de(t)}{dt} \gt 0\)には、D動作出力をプラス方向へ出すことで外乱による変化を抑制する。また、昇温時\(\frac{de(t)}{dt} \lt 0\)では、D動作出力をマイナス方向へ出すことで過昇温（オーバーシュート）を抑制する働きをする。偏差が一定で増加しているとき、D動作出力の値は一定となる。また、偏差が一定（変化がゼロ）のときD動作出力は\(0\)となり、その効果は無くなる。

PIDパラメータの効果

１）比例定数\(K_p = \frac{100}{PB}\)、比例帯\(PB\)［℃］
比例帯\(PB\)を小さくする、すなわち\(K_p\)を大きくすると
・設定値（\SP\)変更への応答は速くなる。
・大きくし過ぎると、応答が振動的になり、ついには不安定になる。
・オフセットが減る。

２）積分時間\(T_i\)
積分時間を短くすると
・オフセットが速く無くなる。
・応答が振動的になり、ついには不安定になる。（位相が遅れるため）

３）微分時間\(T_d\)
微分時間を長くすると
・外乱を速く無くせる。短い周期の外乱の場合は、出力の振れが大きくなる。
・振動的な応答を抑える。長くし過ぎると振動的になり、不安定になる。（高域のゲインが上がるため）

PIDパラメータの最適調整

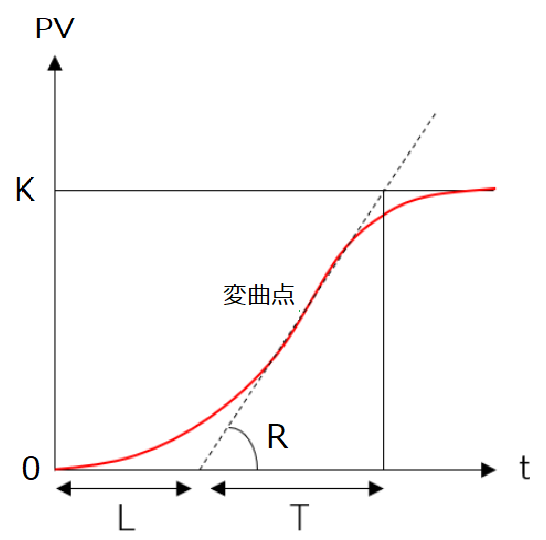
プロセス制御系のステップ応答の多くは、
・定位系（ステップ応答が時間が経てばある値に収束する）
・無定位系（出力がどんどん増大し不安定な応答になる）
となる。
ここでは、定位系におけるPIDパラメータの最適調整を説明する。
図「定位系のステップ応答」で、赤線がプロセスの応答で、変曲点に接線を引き、以下のパラメータを定義する。（注：1次遅れ系のパラメータ定義とは異なる。）
\(K\)：ゲイン
\(T\)：立ち上がり時間（時定数）
\(L\)：むだ時間
\(R=\frac{K}{T}\)：変曲点での接線の傾き
定位系の制御対象の伝達関数\(G_p(s)\)は、1次遅れ系とむだ時間要素で表せる。$$G_p(s) = \frac{K }{1 + Ts}\cdot e^{-sL}$$ \(e^{-sL}\)は有理関数ではないので、古典制御理論の範囲で解析する場合は、マクローリン展開して有理関数に近似して取り扱う。
なお、無定位系の伝達関数は、$$G_p(s) = \frac{R}{s} \cdot e^{-Ls}$$と表せる。

ジーグラ・ニコルスの調整法

PIDパラメータの調整法に関しては、様々な手法が提案されている。どの調整法が一番優れているかは、制御対象の特性に依るところが大きいので一概には言えない。制御理論を理解するという壁があるが、極力、制御対象を数式モデルで表して、周波数応答の検討や、時間応答シミュレーションによりパラメータの妥当性を検証するのが良いと思う。
ここでは、比較的適応し易いとされている代表的なジーグラ・ニコルスの過渡応答法について紹介する。
ジーグラ・ニコルスの過渡応答法では、定位系を対象としてステップ応答の３つのパラメータ\(T\)（立ち上がり時間）、\( K\)（ゲイン）、\( L\)（むだ時間）を基に、PIDパラメータを以下の表に従って調整する。

この他、様々な調整法が提案されている。多数の論文が公開されており、参考サイトなどでまとめて紹介されているので確認して欲しい。

参考サイトなど

化学系のためのPID制御パラメータの調整方法
理化工業株式会社　技術解説
株式会社チノー　8種のPID調整方法
オムロン　FA用語辞典