37. 二自由度制御系
制御の主な目的は、以下のようにまとめられる。
a)制御対象を安定化する
b)外乱の影響を抑制する
c)制御対象の特性変動による影響を抑制する
d)出力を目標値へ追従させる(目標値応答の整形)
a)~c)は主にフィードバック制御で達成し、d)は主にフィードフォワード制御で達成する。
二自由度制御系では、フィードバック制御とフィードフォワード制御を組み合わせることで、a)~d)を成立させる。
二自由度制御系の構成
二自由度制御系の構成は、いろいろな構成があるが、原型としては以下の2種類になる。
1)直列構成
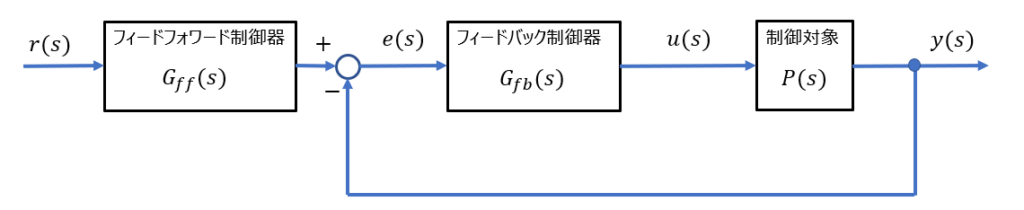
「二自由度制御系 直列構成」のブロック図より、以下の式が成り立つ。
\(e(s) = r(s) G_{ff}(s)- y(s)\) \(y(s) = e(s)G_{fb}(s)P(s)\)
\(y(s) = \left\{r(s)G_{ff}(s) - y(s)\right\}G_{fb}(s)P(s)\) \(y(s)\left\{1 + G_{fb}(s)\right\} = r(s)G_{ff}(s)G_{fb}(s)P(s)\)
よって、 閉ループ伝達関数は、$$T(s) = \frac{y(s)}{r(s)} = \frac{G_{ff}(s)G_{fb}(s)P(s)}{1 + G_{fb}(s)P(s)}$$となる。特性方程式は、\(1 + G_{fb}(s)P(s) = 0\)で、一自由度制御系と同じになる。従って、制御系の安定性の設計条件は一自由度制御系と同じとなる。また、 閉ループ伝達関数から分かるように、出力特性は\(G_{ff}(s)\) (前置制御器)によって調整できることになる。
2)並列構成
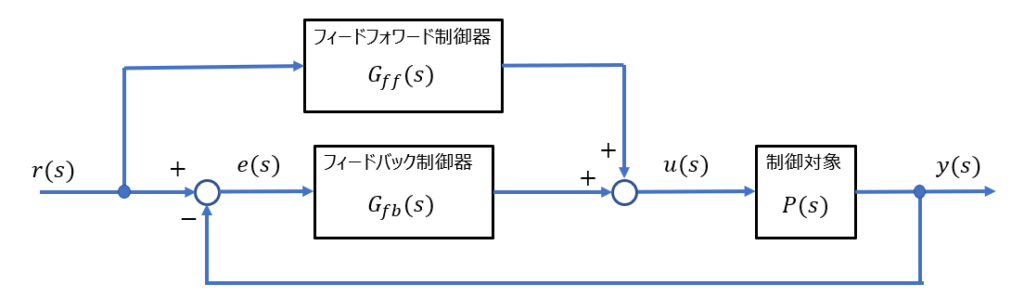
「二自由度制御系 並列構成」のブロック図より、以下の式が成り立つ。
\(e(s) = r(s) - y(s)\) \(y(s) = \left\{e(s)G_{fb}(s) + r(s)G_{ff}(s)\right\}P(s)\)
\(y(s) = (r(s) - y(s)G_{fb}(s)P(s) + r(s)G_{ff}(s)P(s)\) \(y(s)\left\{1 + G_{fb}(s)P(s)\right\} = r(s)\left\{G_{fb}(s) + G_{ff}(s)\right\}P(s)\)
よって、閉ループ伝達関数は、$$T(s) = \frac{y(s)}{r(s)} = \frac{\left\{G_{fb}(s) + G_{ff}(s)\right\}P(s)}{1 + G_{fb}(s)P(s)}$$となる。特性方程式は、\(1 + G_{fb}(s)P(s) = 0\)で、一自由度制御系と同じになる。従って、制御系の安定性の設計条件は一自由度制御系と同じとなる。また、 閉ループ伝達関数から分かるように、出力特性は\(G_{fb}(s) + G_{ff}(s)\) によって調整することになる。
以上のように二自由度制御系は、安定性(位相余裕、利得余裕)と目標値追従特性を個別に設計できるため、効果的な制御手法と言える。制御器をコンピュータで実装する場合は、プログラムの僅かな追加で済むので、積極的に導入して良いと思われる。
モデルマッチング二自由度制御系
モデルマッチング二自由度制御系は、二自由度制御系の直列構成と並列構成を組み合わせたような構成になっているが、出力応答特性を規範モデルに一致させるようになっている。
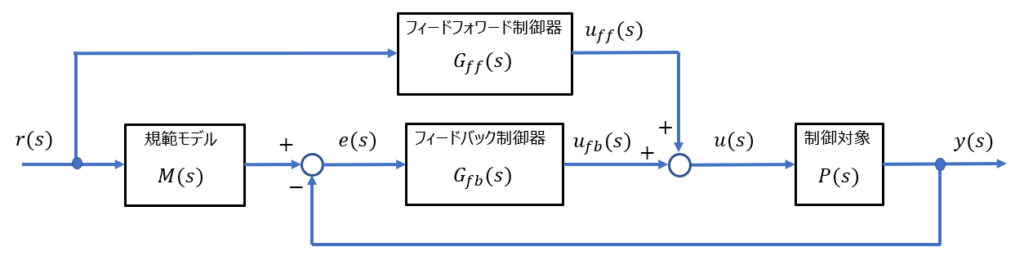
「モデルマッチング二自由度制御系の構成」のブロック図より、
\(e(s) = r(s)M(s) - y(s)\) \(y(s) = \left\{e(s)G_{fb}(s) +r(s)G_{ff}(s)\right\}P(s)\)
\(y(s) = \left\{r(s)M(s) - y(s)\right\}G_{fb}(s)P(s) + r(s)G_{ff}(s)P(s)\)
\(y(s)\left\{1 + G_{fb}(s)P(s)\right\} = r(s)\left\{M(s)G_{fb}(s) + G_{ff}(s)\right\}P(s)\)
よって、閉ループ伝達関数は、$$T(s) = \frac{y(s)}{r(s)} = \frac{\left\{M(s)G_{fb}(s) + G_{ff}(s)\right\}P(s)}{1 + G_{fb}(s)P(s)}$$ $$ = \frac{G_{fb}(s)P(s)}{1 + G_{fb}(s)P(s)} M(s) + \frac{G_{ff}(s)P(s)}{1 + G_{fb}(s)P(s)}$$ となる。特性方程式は、\(1 + G_{fb}(s)P(s) = 0 \)なので、一自由度系の特性方程式と同じである。従って、安定性の設計条件は一自由度系と同じになる。さらに、出力特性は規範モデル\(M(s)\)により望みの応答になるように調整できる。
モデルマッチング二自由度制御系の設計
*設計の手順
1)フィードフォワード制御器\(G_{ff}(s)\)を設計する。
2)フィードバック制御器\(G_{fb}(s)\)を設計する。
ここで、制御対象の伝達関数\(P(s)\)はプロパーとする。
制御対象の特性を\(P(s)\)から規範モデルの\(M(s)\)に整形(マッチング)するように設計する。
※プロパーな伝達関数 とは、「分母の次数≧分子の次数」(因果律)を満たす伝達関数のこと。
1)フィードフォワード制御器\(G_{ff}(s)\)の設計
\(M(s)\)を設計パラメータとして制御対象\(P(s)\) を基に、次の制御入力\(u_{ff}(s)\)となるフィードフォワード制御器\(G_{ff}(s)\)を設計する。$$u_{ff} (s) = \frac{M(s)}{P(s)} r(s) = G_{ff} (s)r(s)$$ $$G_{ff} (s) = \frac{M(s)}{P(s)}$$ 外乱が無いとすると出力は、\(y(s) = u_{ff}(s)P(s) = M(s)r(s)\) となり、出力特性は規範モデルの\(M(s)\)で決まる。
ただし、規範モデルの\(M(s)\)は安定でプロパー、\(G_{ff} (s)\)も安定でプロパーとなるようにする。
2)フィードバック制御器\(G_{fb}(s)\)の設計
制御系の安定性を主として、位相進み補償器などの制御器を設計する。
モデルマッチング二自由度制御系
の設計例
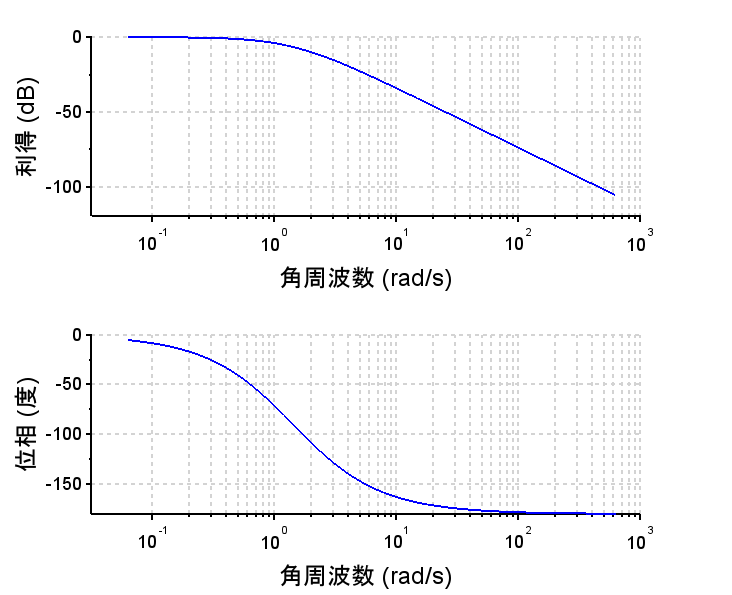
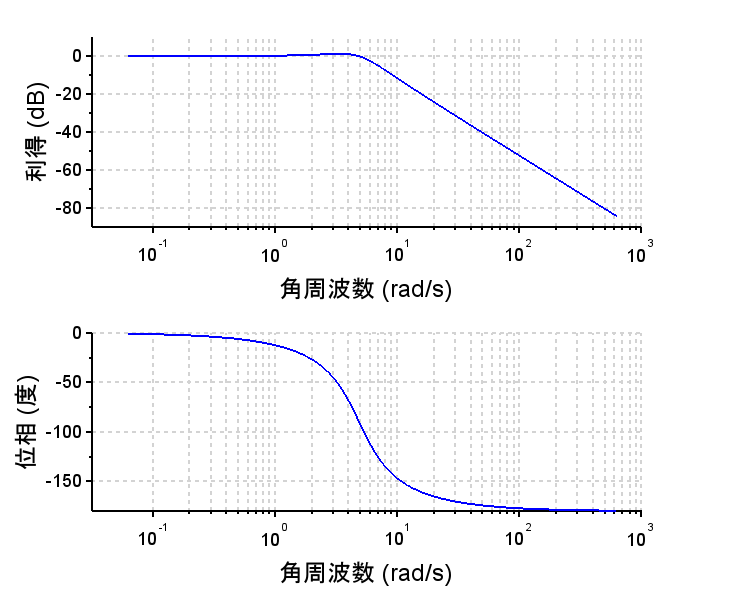
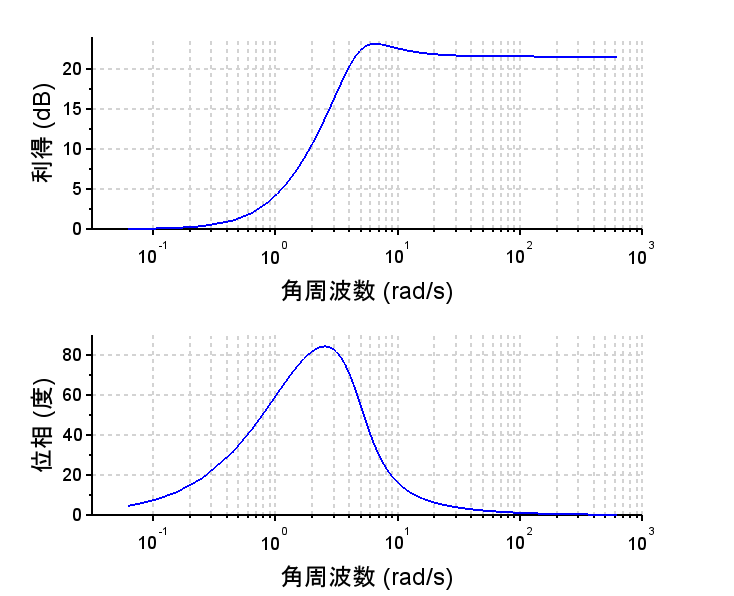
制御対象\(P(s)\)を$$P(s)=\frac{2}{(s+1)(s+2)}$$ 規範モデル\(M(s)\)を$$M(s)=\frac{24}{s^2 + 5s +24}$$とする。
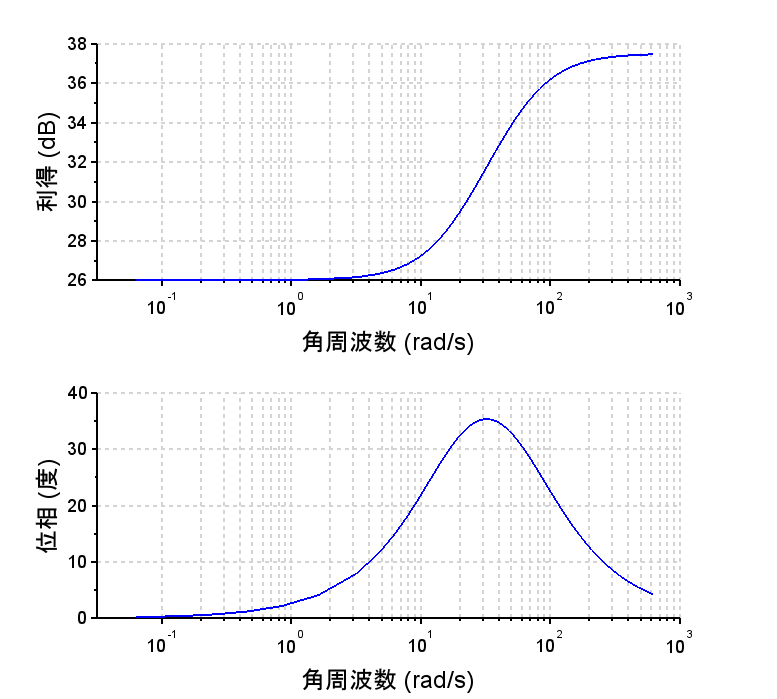
このときフィードフォワード制御器は、$$G_{ff} (s)=\frac{M(s)}{P(s)} =\frac{12(s^2+3s+2)}{s^2+5s+24}$$となる。フィードバック制御器\(G_{fb}(s)\)は、位相進み補償器とする。
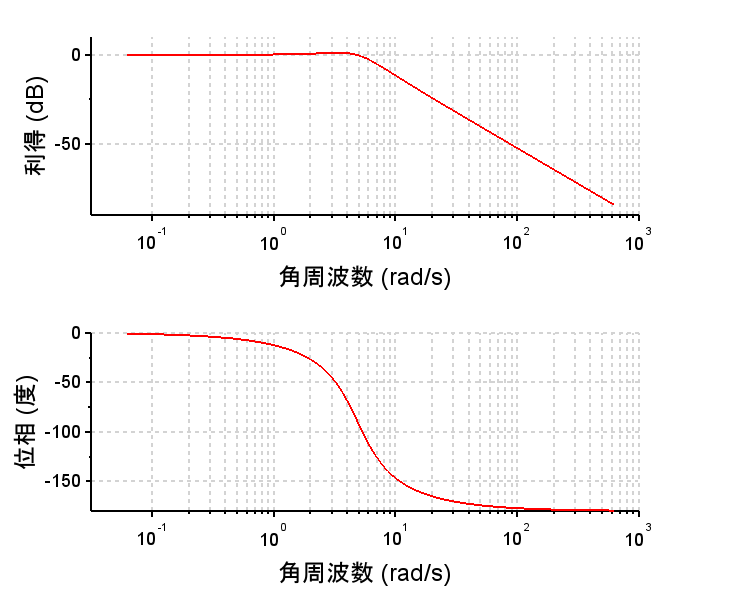
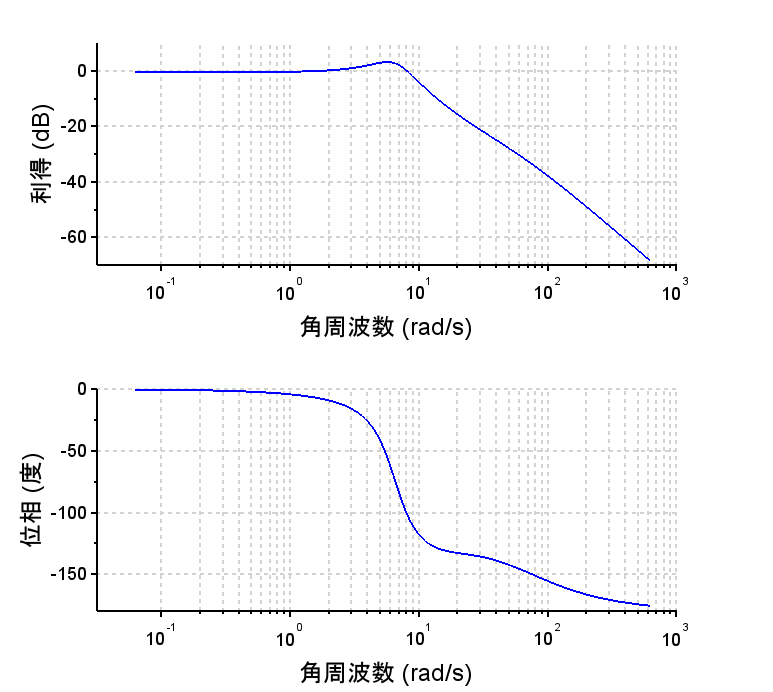
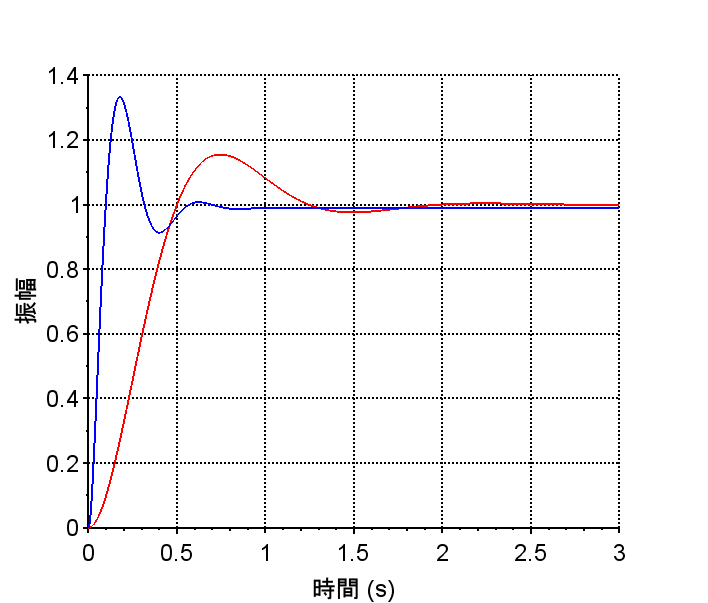
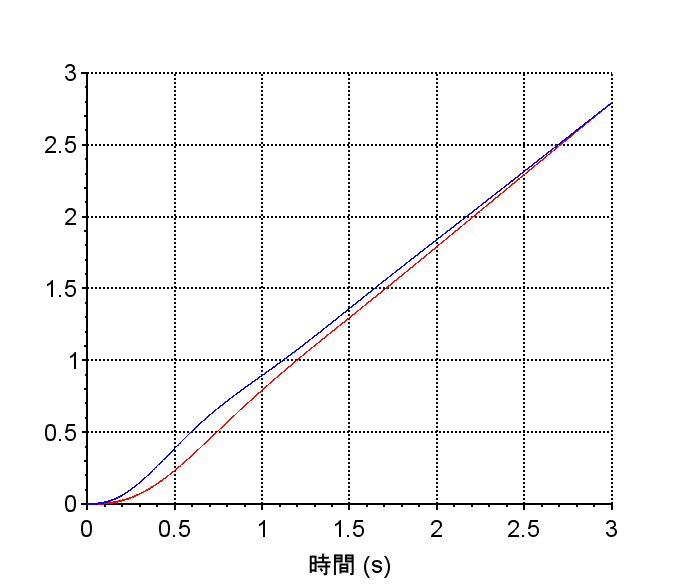
(設計手法はこちらで)$$G_{fb}(s) = \frac{20(0.06s+1)}{0.016s+1}$$ 閉ループ 伝達関数\(T(s)\) の周波数応答は、\(G_{ff} (s) = \frac{M(s)}{P(s)}\)とすると、規範モデル\( M(s)\) に一致する。従って、そのステップ応答は規範モデルの応答となる。「ステップ応答の比較」を見ると、フィードバック制御器\(G_{fb}(s)\)だけを使用した制御系(青線)では、定常位置偏差が残っている。また、「ランプ応答の比較」では、フィードバック制御器\(G_{fb}(s)\)だけを使用した制御系(青線)もモデルマッチング二自由度制御系(赤線)も、定常速度偏差が残っている。これを調整するには規範モデル\(M(s)\)を変更する必要がある。
なお、外乱抑圧特性は基本的にフィードバック制御器\(G_{fb}(s)\)によって決まる。ここでは、簡単な設計例とするために位相進み制御器だけで済ませたが、実際には外乱抑圧特性を考慮したフィードバック制御器\(G_{fb}(s)\)の検討が必要である。
Scilabスクリプト
//モデルマッチング2自由度制御系の例
clear;clf;
s=%s;
//制御対象
P=2/((s+1)*(s+2));
Ps=syslin('c',P);
//規範モデル
M=24/(s^2+5*s+24);
Ms=syslin('c',M);
//制御対象のボード線図
scf(0);
bode(Ps,10^-2,10^2,'rad');
//規範モデルのボード線図
scf(1);
bode(Ms,10^-2,10^2,'rad');
//フィードフォワード制御器
Gff=M/P;
Gffs=syslin('c',Gff);
scf(2);
bode(Gffs,10^-2,10^2,'rad');
//フィードバック制御器(位相進み制御器)
Gfb=20*(0.06*s+1)/(0.016*s+1);
Gfbs=syslin('c',Gfb);
scf(3);
bode(Gfbs,10^-2,10^2,'rad');
//閉ループ伝達関数
T=Gfb*P*M/(1+Gfb*P)+Gff*P/(1+Gfb*P);
Ts=syslin('c',T);
scf(4);
bode(Ts,10^-2,10^2,'rad');
//フィードバック制御器だけの場合
T1=Gfb*P/(1+Gfb*P);
T1s=syslin('c',T1);
scf(5);
bode(T1s,10^-2,10^2,'rad');
//ステップ応答の比較
t=0:0.001:3;
scf(6);
y=csim('step',t,Ts);
y1=csim('step',t,T1s);
plot2d(t,y,5);
plot2d(t,y1,2);xgrid;
//ランプ応答の比較
t=0:0.001:3;
scf(7);
yr=csim(t,t,Ts);
yr1=csim(t,t,T1s);
plot2d(t,yr,5);xgrid;
plot2d(t,yr1,2);

