40. モータのモデル化(2)
電気ー機械系の典型である電気モータの数学モデルに関して説明する。リニア型モータとロータリー型モータについてその数式モデルを考える。
リニア型(非回転型)モータ
モータのモデルとして比較的簡単なリニア型(非回転型)モータについて、その数式モデルを説明する。リニア型モータの例としてHDD(Hard Disk Drive)のアクチュエータとして使われているVCM(ボイスコイルモータ)を紹介する。

HDDで使用するVCMの特徴は、
1)可動部が軽量なコイルのみのため高速な応答が得られる
2)ヒステリシスが小さく、電流と推力の関係が直線状で良好な制御性をもつ
3)双方向駆動が可能なため、位置決め制御に向いている
である。
VCMの動作原理
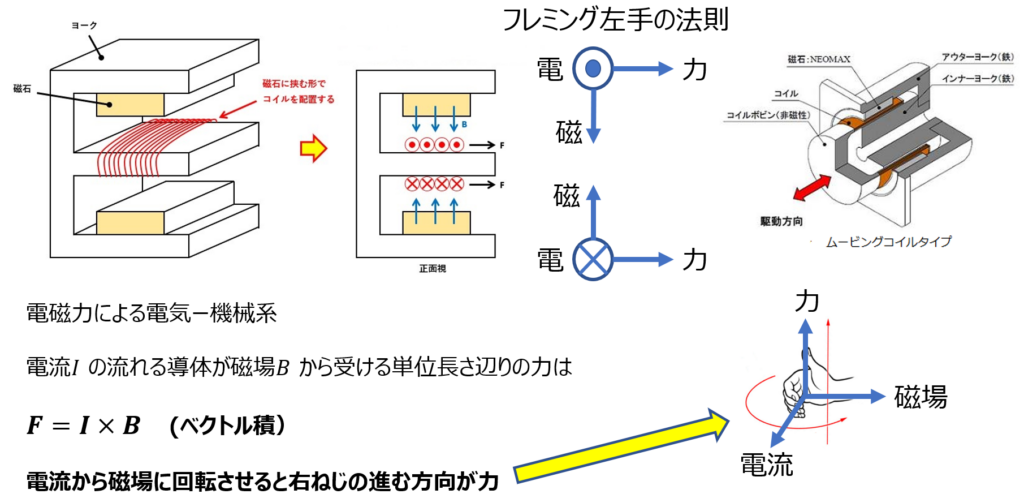
〇の中に✕は電流が画面の表から裏に向かっていることを表している。
VCMの動作は、フレミングの左手の法則にしたがう。構造としては、通常、コイルが動く、ムービングコイルタイプが使われる。ムービングコイルタイプは、可動部が軽量なため応答特性に優れている。(コイルを固定にして磁石が動く構成のものもある。)
「フレミング左手の法則」の図で、「磁」は磁場の方向を表しており、コイルは図のように巻いているので、上側と下側で電流の流れる方向が逆になる。磁場の方向と電流の方向からコイルに働く力の方向は同じになり、コイルが一方向に移動する。電流の方向を逆にするとコイルの移動方向は逆になる。
VCMの数式モデル
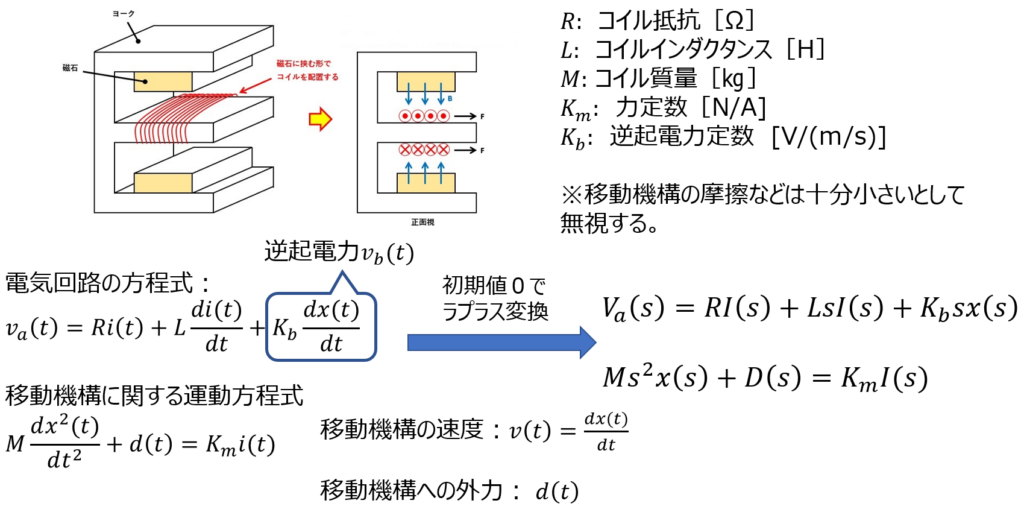
電気回路の方程式で、\(v_b(t)\)はコイルの移動に伴う逆起電力である。これは磁場中でコイルが動くことで生じる起電力でフレミングの右手の法則に従う(発電機の原理)。 この逆起電力は、コイルの移動速度に比例するため、速度\(v(s)\)が速いほど大きくなるので、ダンパーとして働くことになる。
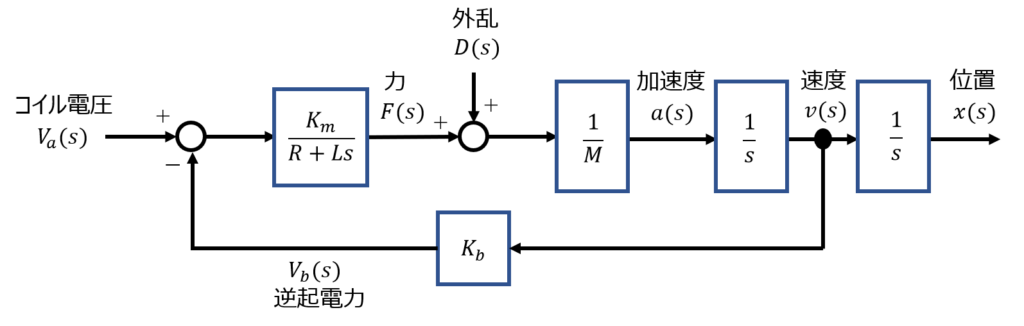
\(D(s)=0\)として考える。$$F(s)=\frac{K_m}{R + Ls}\left\{V_a(s) - V_b(s)\right\}$$ $$x(s) =\frac{F(s)}{Ms^2} \enspace \enspace F(s)=Ms^2 x(s) \enspace \enspace V_b(s) = K_bv(s) = K_bsx(s)$$ 一般に機械系の時定数に比較して、電気系の時定数は十分に小さいので、\(L \approx 0\)とみなせる。従って、$$Ms^2x(s) = \frac{K_m}{R}V_a(s) - \frac{K_m}{R}V_b(s) = \frac{K_m}{R}V_a(s) - \frac{K_m}{R}K_bsx(s)$$ $$\left\{Ms^2 + \frac{K_mK_b}{R}s\right\}x(s) = \frac{K_m}{R}V_a(s) \enspace \enspace (K=K_m=K_b)$$ また、時定数:\(\tau \left[s\right]\) \(\tau = \frac{MR}{K^2}\)である。
伝達関数は、$$G(s) = \frac{x(s)}{V_a(s)} = \frac{\frac{K}{R}}{Ms^2 + \frac{K^2}{R}s} = \frac{K}{MRs^2 +K^2s}$$ $$=\frac{K}{s(MRs + K^2)} = \frac{\frac{1}{K}}{s\left(\frac{MR}{K^2}s +1\right)} = \frac{\frac{1}{K}}{s(\tau s +1)}$$である。以上より、VCMへの入力電圧から変位(位置変化)までの伝達関数は、$$G(s)=\frac{\frac{1}{K}}{s(\tau s +1)}$$ となる。
この伝達関数は、基本構造の伝達関数で、実際には機構の高次機械共振などが付加される。
DCサーボモータの数式モデル
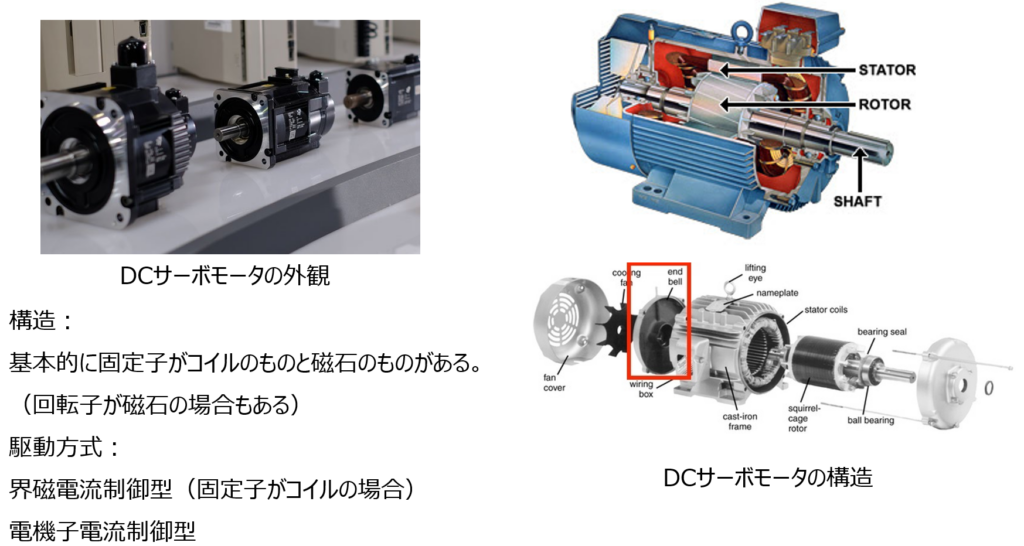
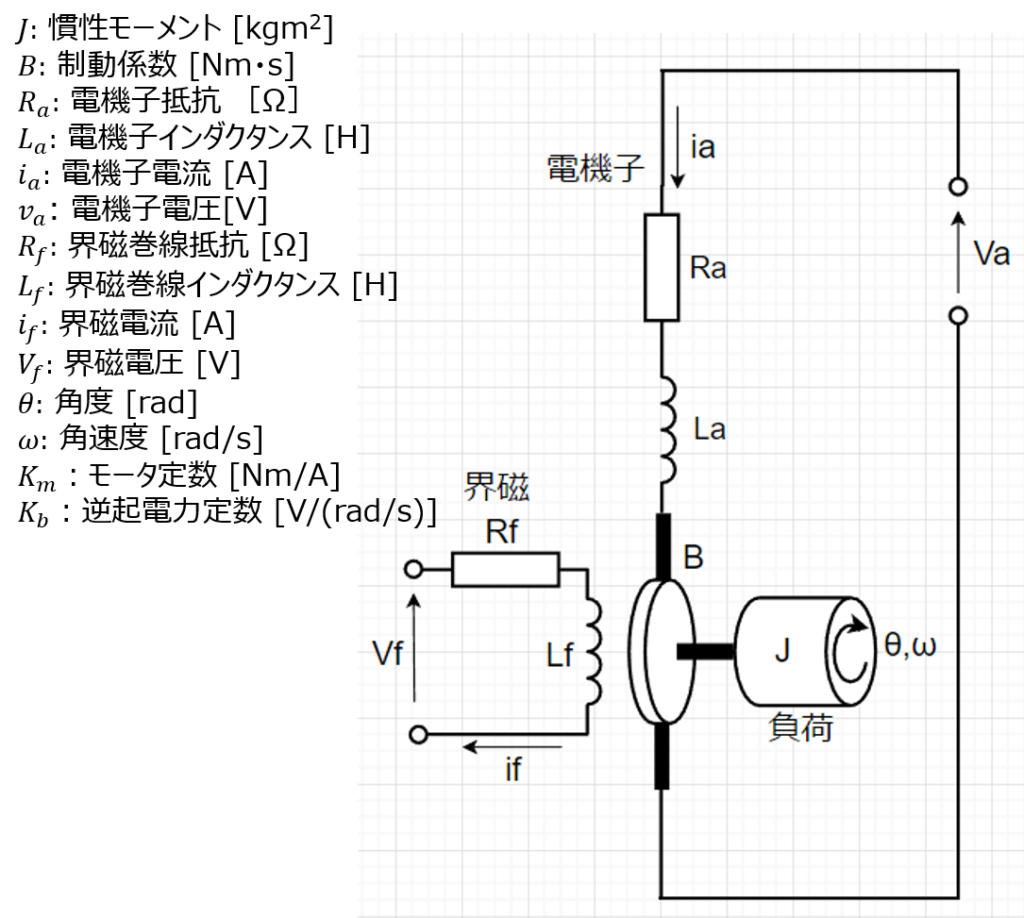
DCサーボモータには様々なタイプがあるが、駆動方式で分類すると、界磁電流制御型と電機子電流制御型に分かれる。ここでは、この2方式のモデルを紹介する。
DCモータトルクの微分方程式
トルクと負荷の関係は、モータ回転機構部の慣性モーメント及び、動摩擦力から、$$\omega(t)=\frac{d\theta(t)}{dt}$$として、$$T_L(t)=J\frac{d\omega(t)}{dt} + B\omega(t)$$ 初期値を\(0\)として、両辺をラプラス変換すると、$$T_L(s)=Js\Omega(s) + B\Omega(s)$$ $$= Js^2\Theta(s) + Bs\Theta(s)$$となる。
注)ここでは、数式モデルの基本として、磁気回路のヒステリシスやブラシ(電機子)における電圧降下などは、無視できるものとする。
慣性モーメント(イナーシャ)、トルク
・慣性回転体のモーメント \(J \left[kg\cdot m^2\right]\)
慣性モーメント\(J\)の基本は、回転体の中心を回る「回転体の質量\(M \left[kg\right]\)と回転体の半径\(R\left[m\right]\)の2乗との積」である。$$J=M\times R^2$$
・回転トルク \(\tau \left[N\cdot m\right]\)
イナーシャ\(J\) の回転体に角加速度\(\alpha=\frac{d^2\theta(t)}{dt^2} \left[rad/s^2\right]\) を生じさせるにはトルク\(\tau \left[N\cdot m\right]\)が必要となる。$$\tau = J \times \alpha$$
※力 \(F=m\times a\) \(m\):質量\(\left[kg\right]\) \(a\):加速度\(\left[ m/s^2\right]\)
界磁電流制御方式のモデル
以下モータトルクなどはラプラス変換形式で表すこととする。
電機子電流は定電流(\(i_a(t)=I_a\) :一定の電流値)なので、$$T_m (s)=(K_1 K_f I_a ) I_f (s)=K_m I_f (s)$$となる。界磁電流は界磁印可電圧により決まるので、$$V_f(t) = R_f i_f (t) + L_f\frac{ di_f (t)}{dt}$$である。これをラプラス変換して、界磁電流を求めると $$I_f (s)=\frac{1}{R_f+L_f s} V_f (s)$$と表せる。また、負荷トルクはモータ回転機構部の慣性モーメント及び、動摩擦力から $$T_L (s)=Js^2\Theta (s)+Bs\Theta (s) = Js\Omega(s)+B\Omega(s)$$と表せる。

外乱トルク\(T_d (s)\)とすると\(T_L (s)=T_m (s) - T_d (s)\)である。\(T_d (s)=0\)とすると、$$T_L (s)=Js^2 \Theta (s)+Bs\Theta(s) =T_m (s) = K_m I_f (s)$$ \(\Theta(s) = \frac{K_m}{s(Js+B)} I_f (s)\) また、\(V_f (s)=(R_f+L_f s)I_f (s)\) 以上より、$$G(s)=\frac{\Theta(s)}{V_f (s)} = \frac{K_m}{s(Js+B)(L_f s+R_f)} $$ $$=\frac{\frac{K_m}{J L_f}}{s(s +\frac{B}{J})(s + \frac{R_f}{L_f})}$$ 界磁時定数(電気系時定数)\(\tau_f = \frac{L_f}{R_f}\) 機械系時定数 \(\tau_L = \frac{J}{B}\) とおくと、$$G(s) = \frac{ \frac{K_m}{BR_f}}{ s (\tau_f s+1)(\tau_L s+1)}$$ \(\tau_L \gt \tau_f\) なので、多くの場合界磁時定数は無視できる。
電機子電流制御方式のモデル
界磁電流は定電流(\(i_f(t)=I_f\):一定の電流値)なので、$$T_m (s) = (K_1 K_f I_f ) I_a (s) = K_m I_a (s)$$ 電機子電圧は電機子印可電圧と逆起電力\(V_b (s)\)から決まるので、$$V_a (s)=(R_a + L_a s) I_a (s)+V_b (s) \enspace \enspace V_b (s) = K_b \omega(s)$$ よって、$$I_a (s)=\frac{V_a (s)-K_b \omega(s)}{R_a+L_a s}$$
負荷トルクはモータ回転機構部の慣性モーメント及び、動摩擦力から$$T_L (s) = Js^2 \Theta(s)+Bs\Theta(s)=T_m (s) - T_d (s)$$
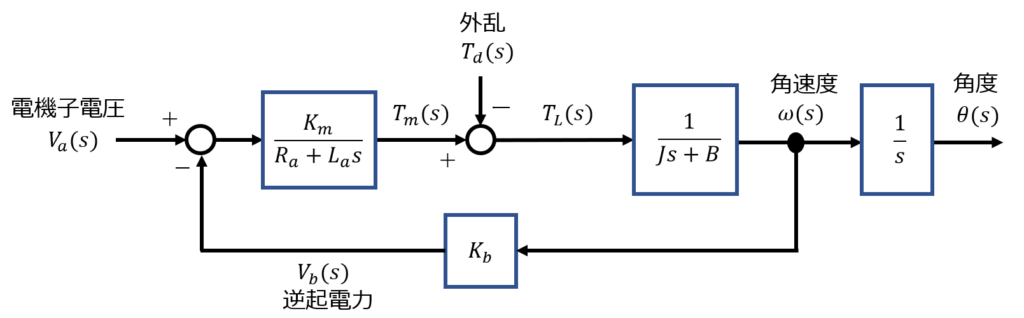
\(T_d (s) = 0\)とすると、$$G(s)=\frac{\Theta(s)}{V_a (s)} = \frac{K_m}{s[(R_a+L_a s)(Js+B)+K_b K_m ]}$$ $$=\frac{K_m}{s(s^2+2 \zeta \omega_n s+\omega_n^2 )}$$ 電機子時定数(電気系時定数) \(\tau_a = \frac{L_a}{R_a}\) であるが、多くの場合、電機子時定数は無視できるので、\(L_a=0\)として、$$G(s)=\frac{\Theta(s)}{V_a (s)} = \frac{K_m}{s[R_a (Js+B)+K_b K_m ]}$$ $$=\frac{[\frac{K_m}{(R_a B+K_b K_m ) }]}{s(\tau_1 s+1)}$$となる。ここで、\(\tau_1 = \frac{R_a J}{(R_a B+K_b K_m )}\)である。
さらに\(K = \frac{K_m}{R_aB + K_bK_m}\) \(K_m = K_b\)とすると、$$G(s) = \frac{K}{s(\tau_1 s + 1)}$$ と表せる。
単位について
*トルクの単位
トルクの単位は以前はkgf・m(重力単位系)が用いられていたが、1993年に施行された「新計量法」によりSI単位(ISO国際規格)への移行が義務づけられ、現在では力の単位はN(ニュートン)、トルクの単位はN・m(ニュートンメートル)となっている。
旧型のモータなどでは、重力単位系が使われているものがあり、慣性モーメントを\(GD^2\)で表している場合があるので注意が必要である。
\(GD^2=\)(重量) × (回転直径)2 [kgf・m2] \(J= \frac{GD^2}{4}\) (重力単位ではない)
※ J = (質量) × (回転半径)2 [kg・m2]


“40. モータのモデル化(2)” に対して1件のコメントがあります。
コメントは受け付けていません。