42. DCモータの制御(1)
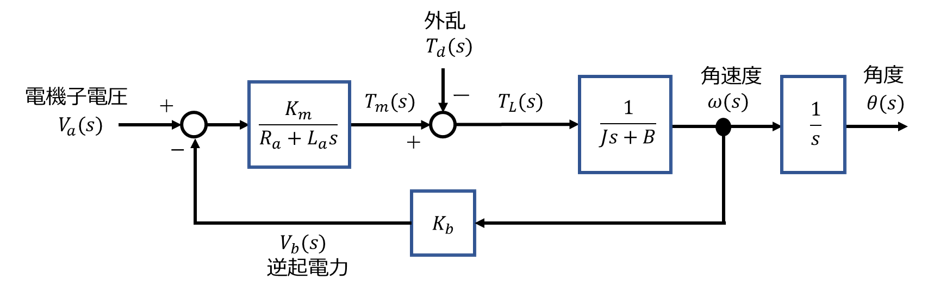

DCモータの伝達関数
*電機子電圧ー角速度 伝達関数 $$P1(s) = \frac{\omega(s)}{V_a(s)} = \frac{K_m}{R_a (Js+B)+K_b K_m } $$ $$= \frac{K}{τ_1 s+1}$$ 時定数:\(\tau_1=\frac{R_a J}{R_a B+K_b K_m }\)
\(K = \frac{K_m}{R_a B+K_b K_m }\) \(K_m = K_b\)
*電機子電圧ー角度 伝達関数 $$P2(s)=\frac{θ(s)}{V_a (s)} = \frac{K_m}{s\left[R_a (Js+B)+K_b K_m \right]}$$ $$=\frac{\frac{K_m}{R_a B+K_b K_m }}{s(\tau_1 s+1)} = \frac{K}{s(\tau_1 s+1)}$$
※基本的にはVCMの制御と同様な制御手法が使用できるが、DCモータのような回転系の場合、ロータリーエンコーダ、タコジェネレータのようなセンサで比較的容易に回転角度、回転速度を検出(測定)できるため、速度フィードバックを実装しやすい。
DCモータの特性
【例】小型DCモータ
回転子イナーシャ \(J\):1.0e-3 [kg・m2]
トルク定数 (\(K_m\),\(K_b\)):50.0e-3 [Nm/A]
機械的時定数 \(\tau_1\):0.1 [s]
※電気的時定数は、1 [ms] と \(\tau_1\) より十分小さいので無視する。
$$\tau_1 = \frac{R_a J}{R_a B+K_b K_m }=0.1$$ $$K = \frac{K_m}{R_a B+K_b K_m }\approx \frac{1}{K_m}=20 \enspace \enspace (K_m=K_b)$$
以下のモデルを制御系設計に使用する。
*電機子電圧ー角速度(回転速度) 伝達関数 $$P1(s)=\frac{\omega(s)}{V_a (s)}=\frac{20}{0.1s+1}$$ * 電機子電圧ー角度(回転角度) 伝達関数 $$P2(s)=\frac{\theta(s)}{V_a (s)}=\frac{20}{s(0.1s+1)}$$
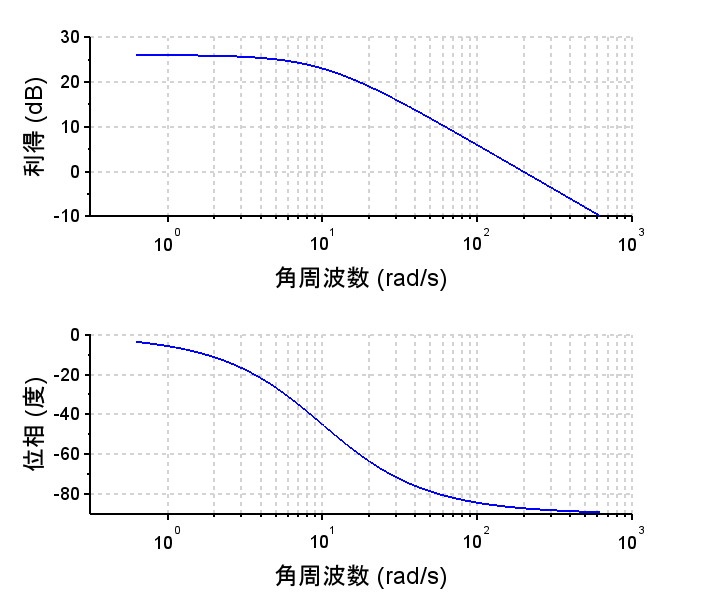
周波数特性
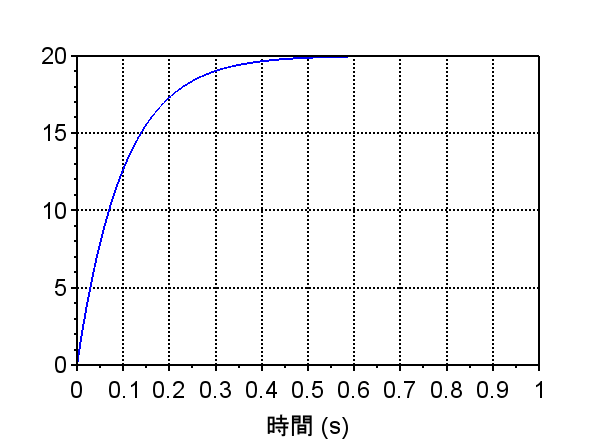
ステップ応答
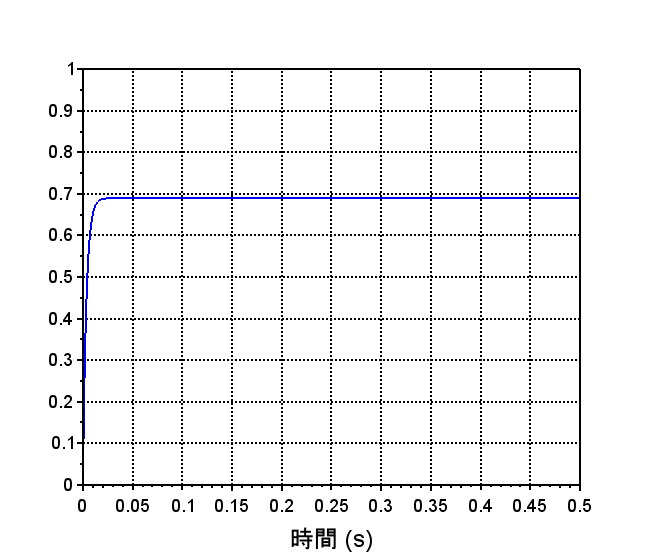
電機子電圧ー角速度(回転速度)の特性
$$P1(s)=\frac{\omega(s)}{V_a (s)}=\frac{20}{0.1s+1}$$
•伝達関数、周波数特性より一次遅れ系となっている。
•ステップ応答より一定電圧を印可することで一定速度になる。
•立ち上がり時間(時定数)は逆起電力によって影響を受ける。
•周波数特性より10[rad/s]以上で\(\frac{1}{s}\)(-20dB/dec)特性になっている
DCモータの速度制御系の設計
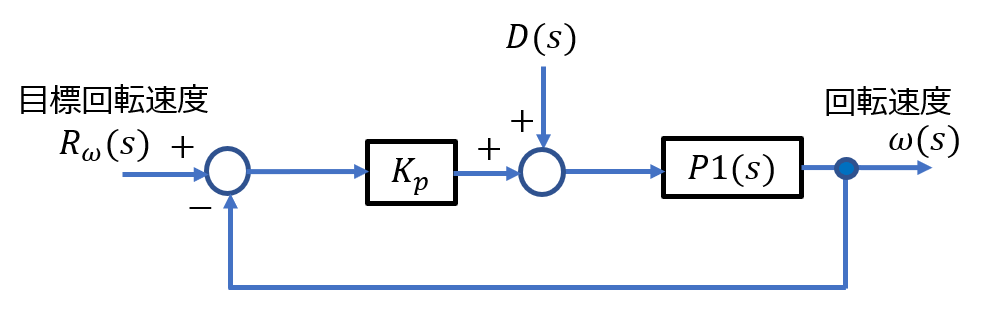
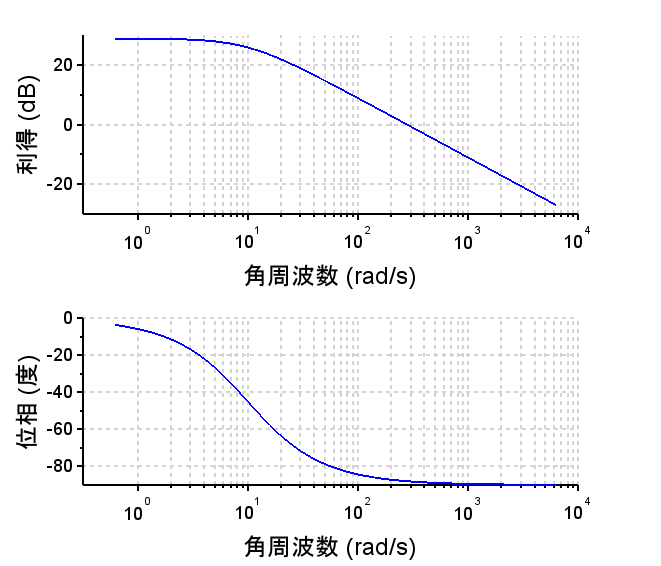
ゲイン補償(\(K_p=1.4\))
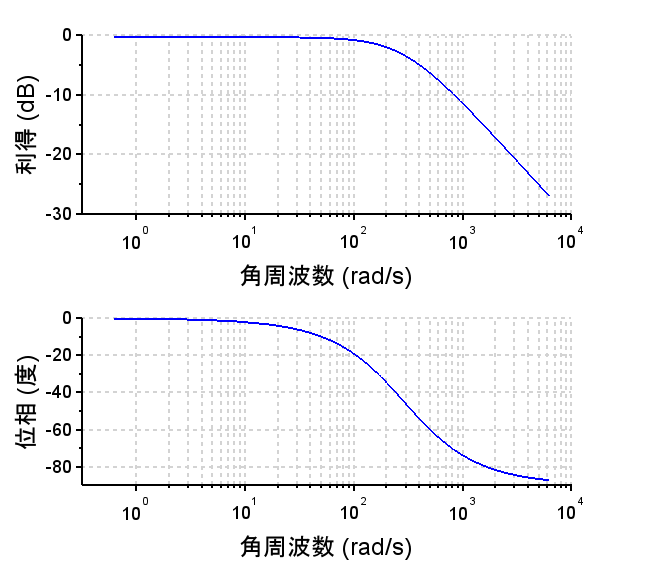
ゲイン補償(\(K_p=1.4\))
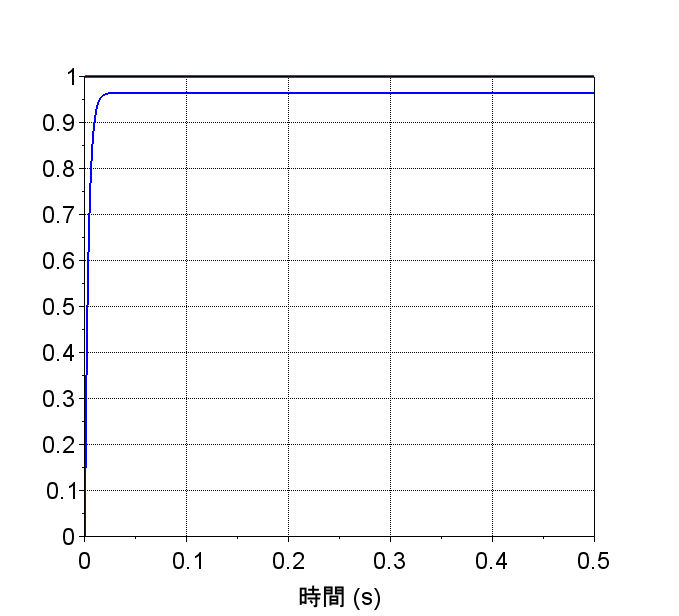
ゲイン補償(\(K_p=1.4\))
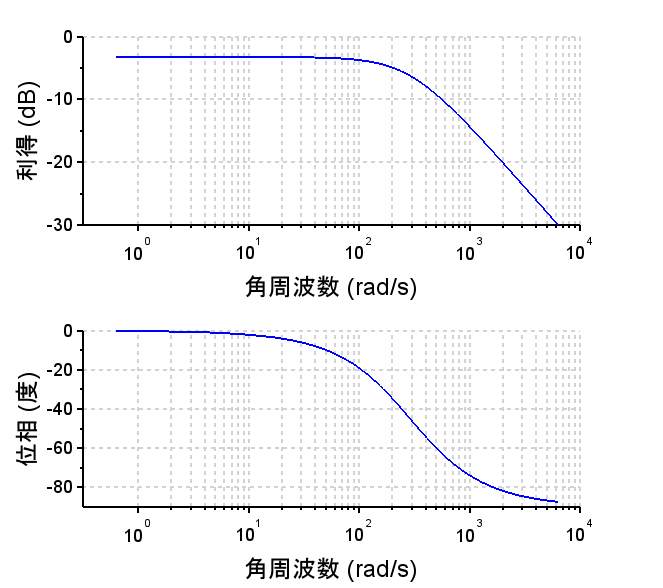
ゲイン補償(\(K_p=1.4\))
ゲイン補償(\(K_p=1.4\))
*ゲイン補償(比例制御)の場合
\(C(s)=K_p\) (ゲイン補償:比例制御)
※目標値応答特性 $$T(s)=\frac{\omega(s)}{R_\omega (s)} =\frac{K_pP1(s)}{1+K_pP1(s)} $$ $$= \frac{K_p \frac{K}{\tau_1 s+1}}{1+K_p \frac{K}{\tau_1 s+1}}= \frac{K_pK}{\tau_1 s+1+K_pK} $$ $$= \frac{K_pK}{1+K_pK}\cdot \frac{1}{\frac{\tau_1}{1+K_pK} s+1}$$ $$L(s) = \frac{K_p K}{\tau_1 s+1}$$
・目標値応答特性、外乱抑圧特性ともに1次遅れ系となって比例ゲイン\(K_p\) を調整すると閉ループ伝達関数の時定数(\(\frac{\tau_1}{1+K_pK}\))が小さくなり応答特性が向上する。
・開ループ伝達関数は0型のため定常偏差が残る。
※外乱抑圧特性 $$\frac{\omega(s)}{D (s)} = \frac{P1(s)}{1+K_pP1(s)} =\frac{\frac{K}{\tau_1 s+1}}{1+K_p \frac{K}{\tau_1 s+1}}$$ $$= \frac{K}{\tau_1 s+1+K_pK}$$ $$= \frac{K}{1+K_pK}\cdot \frac{1}{\frac{\tau_1}{1+K_pK} s+1}$$・低域での外乱抑圧は不十分なため、ステップ状の外乱が入った場合、時間が経過してもその影響が残る。
・外乱抑圧特性に関しては比例ゲイン\(K_p\)を大きくとると影響が小さくなる。ただし、制御帯域が高くなるため、雑音などには弱くなる。
ゲイン補償+積分補償
(\(K_p=1.4\),\(K_i=20\))
ゲイン補償+積分補償
(\(K_p=1.4\),\(K_i=20\))
ゲイン補償+積分補償
(\(K_p=1.4\),\(K_i=20\))
ゲイン補償+積分補償
(\(K_p=1.4\),\(K_i=20\))
ゲイン補償+積分補償
(\(K_p=1.4\),\(K_i=20\))
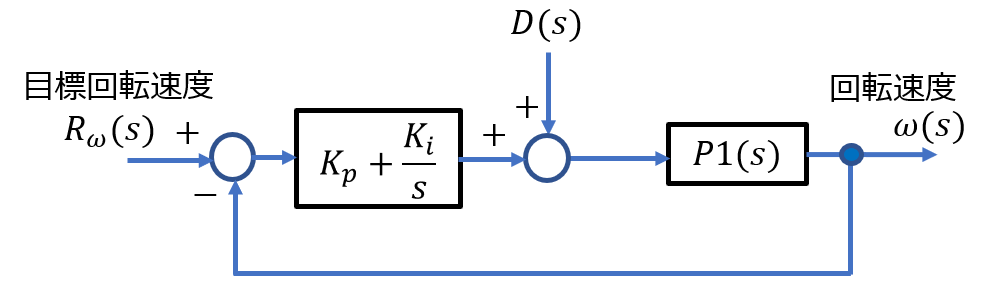
*ゲイン補償+積分補償の場合
\(C(s)=K_p + \frac{K_i}{s}\) (ゲイン補償+積分補償)
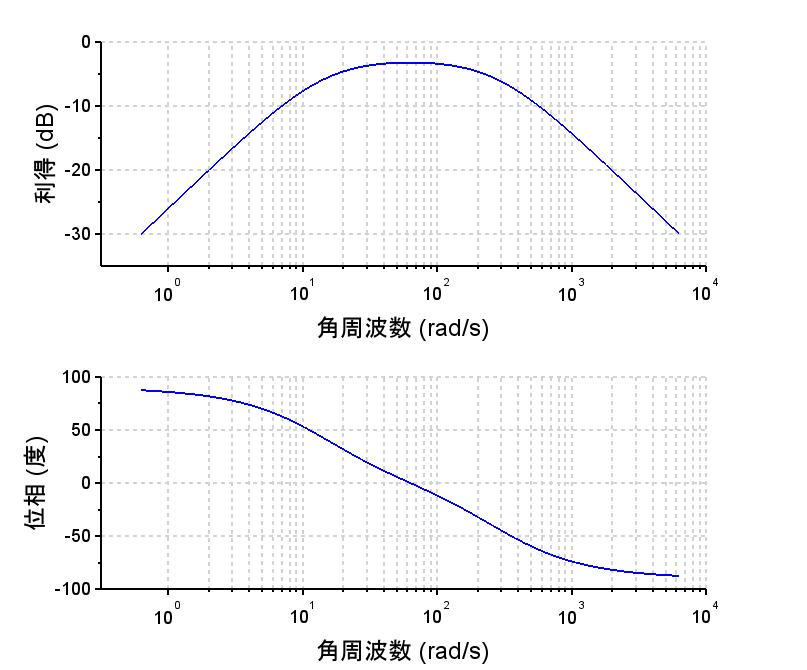
※目標値応答特性 $$T(s)=\frac{\omega(s)}{R_\omega(s)} =\frac{(K_p + \frac{K_i}{s})P1(s)}{1+(K_p + \frac{K_i}{s})P1(s)} $$ $$= \frac{(\frac{K_p s+K_i}{s}) \frac{K}{\tau_1 s+1}}{1+(\frac{K_p s+K_i}{s}) \frac{K}{\tau_1 s+1}}$$ $$=\frac{K_p Ks+K_i K}{\tau_1 s^2+(1+K_p )s+K_i K}$$ $$L(s)=\left(\frac{K_p s+K_i}{s}\right)\frac{K}{\tau_1 s+1}$$・目標値応答特性、外乱抑圧特性ともに2次遅れ系となり、減衰比\(\zeta\)は主に比例ゲイン\(K_p\)、固有周波数\(\omega_n\)は積分ゲイン\(K_i\)により設定できる。
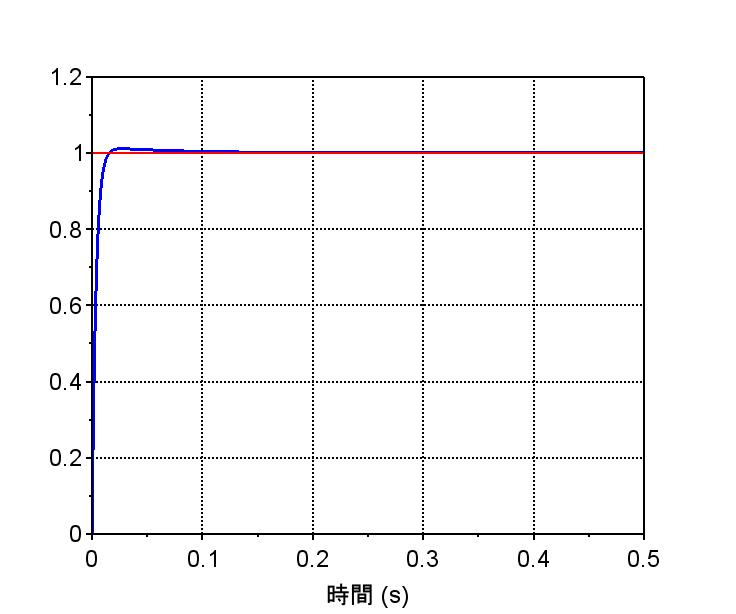
・開ループ伝達関数が1型となるためステップ状の目標速度に対して定常偏差のない制御が実現できる。
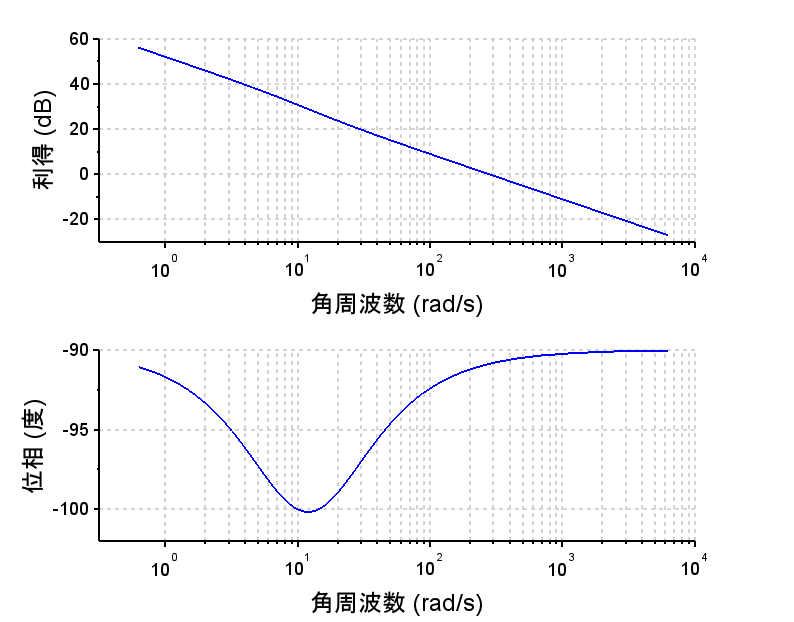
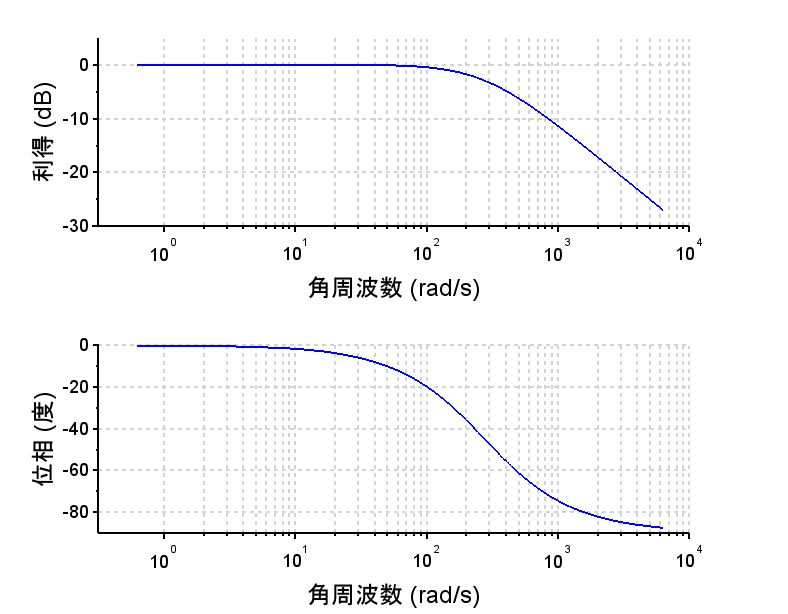
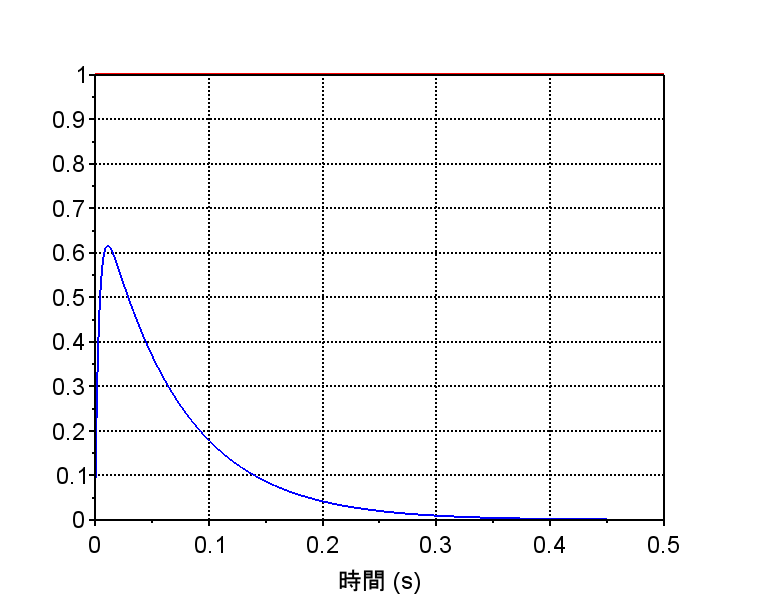
*外乱抑圧特性 $$\frac{\omega(s)}{D (s)} =\frac{P1(s)}{1+L(s)}$$ $$=\frac{\frac{K}{\tau_1 s+1}}{1+(\frac{K_p s+K_i}{s})\frac{K}{\tau_1 s+1}}$$ $$=\frac{Ks}{\tau_1 s^2+(1+K_p )s+K_i K}$$・外乱抑圧は100[rad/s]以上の帯域では、ゲイン補償だけの場合と差はないが、低域での抑圧特性に優れている。その結果、外乱がステップ状に入った場合、時間の経過とともに外乱の影響を0にできている。
・外乱抑圧では積分ゲイン\(K_i\)を十分大きくとると、回転速度に対する外乱の影響を小さくできる。
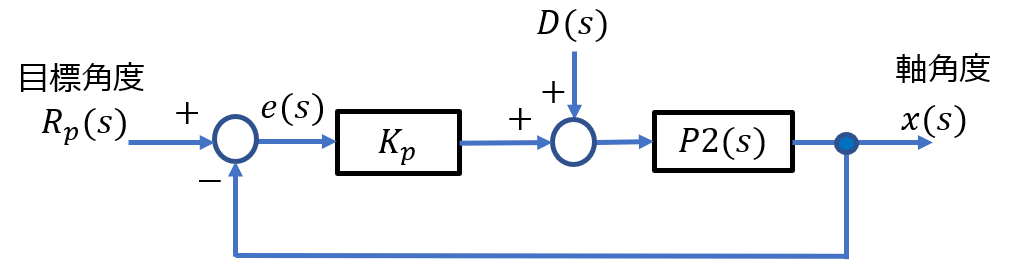
DCモータの位置制御系の設計
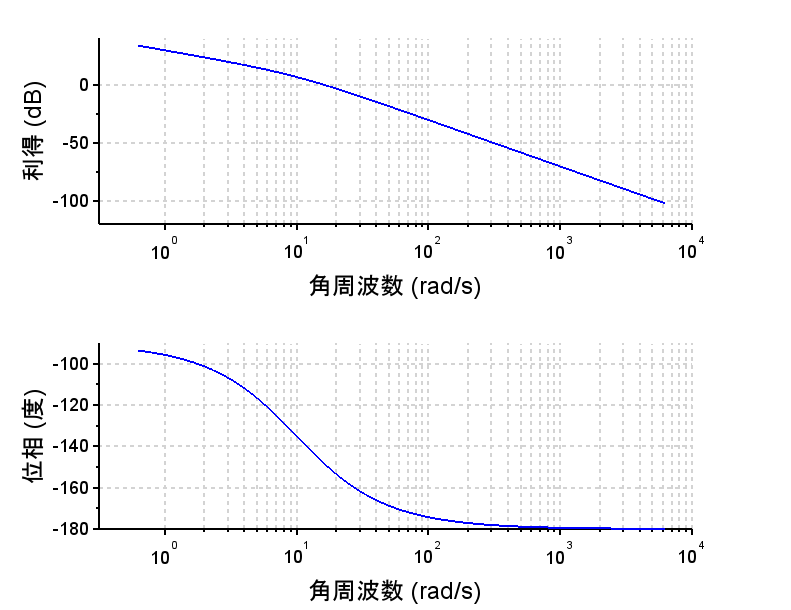
ゲイン補償(\(K_p=1.5\))
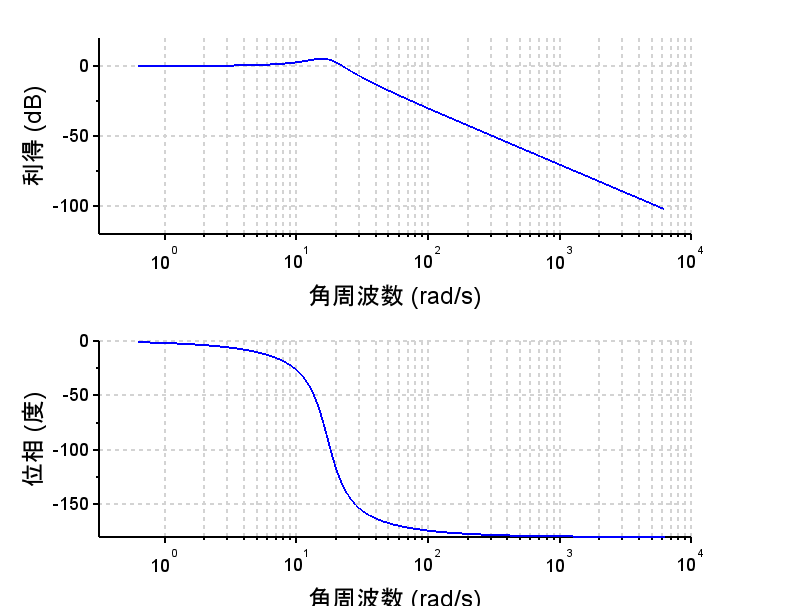
ゲイン補償(\(K_p=1.5\))
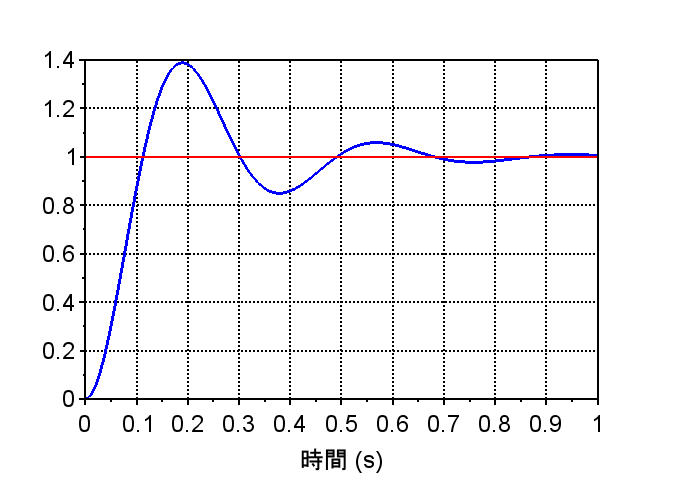
ゲイン補償(\(K_p=1.5\))
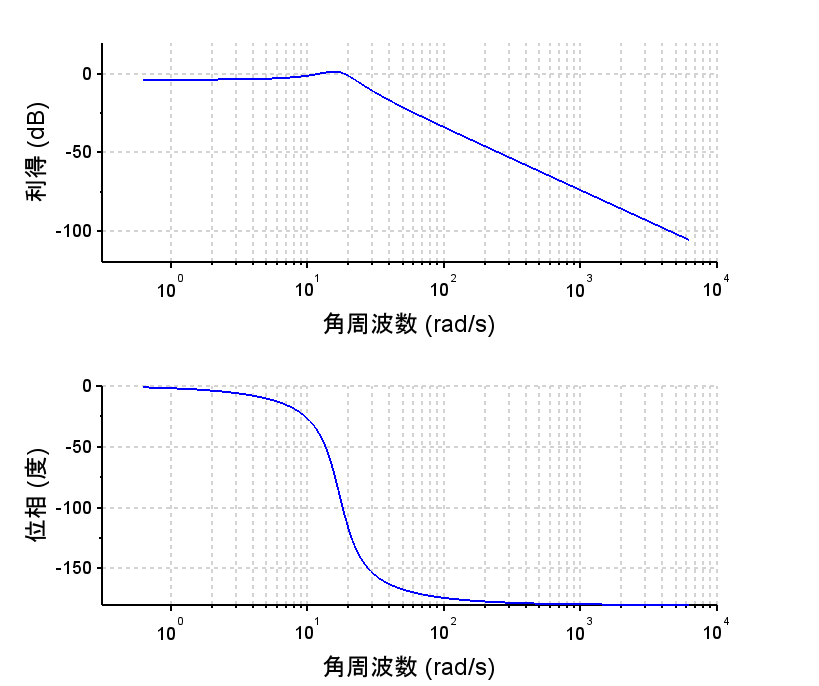
ゲイン補償(\(K_p=1.5\))
ゲイン補償(\(K_p=1.5\))
*ゲイン補償の場合
\(C(s)=K_p\) (ゲイン補償)
※目標値応答特性 $$T(s) = \frac{\omega(s)}{R_\omega (s)} =\frac{K_pP2(s)}{1+K_pP2(s)}$$ $$=\frac{K_p \frac{K}{s(\tau_1 s+1)}}{1+K_p \frac{K}{s(\tau_1 s+1)}}$$ $$=\frac{K_pK}{\tau_1 s^2+s+K_pK}$$ $$L(s)=K_p\frac{K}{s(\tau_1 s+1)}$$ ・開ループ周波数特性から位相余裕が約\(40\text{°}\)であり、これ以上ゲインを高くすることはできない。
・開ループ伝達関数が1型のため定常位置偏差は0となる。
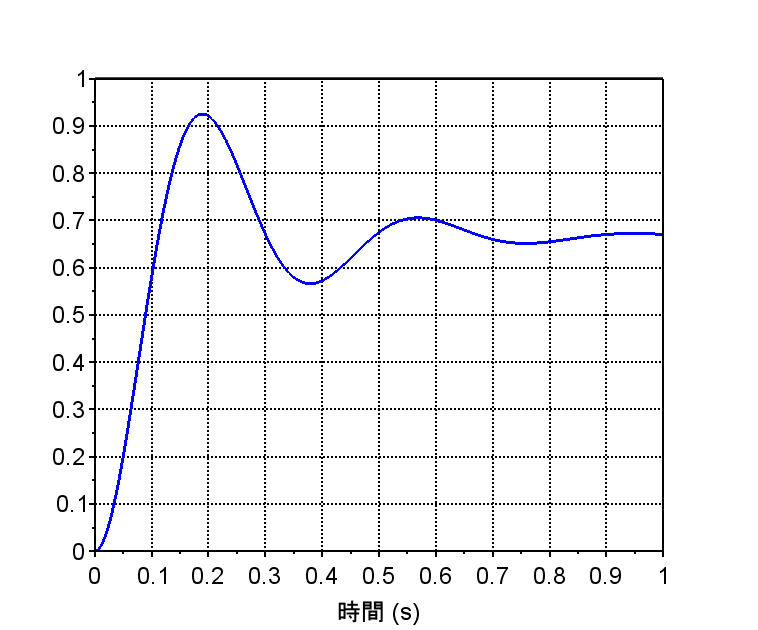
・ステップ応答から定常位置偏差は\(0\)であるが、行き過ぎ量が大きく、整定に時間がかかっている。
・比例ゲイン\(K_p\) を調整すると固有周波数\(\omega_n\)が調整でき、応答特性の振動を変えることができる。
*外乱抑圧特性 $$\frac{\omega(s)}{D (s)} = \frac{P2(s)}{1+K_pP2(s)}$$ $$=\frac{\frac{K}{s(\tau_1 s+1)}}{1+K_p \frac{K}{s(\tau_1 s+1)}}$$ $$=\frac{K}{\tau_1 s^2+s+K_pK}$$ ・目標値応答特性、外乱抑圧特性ともに2次遅れ系となる。
・外乱抑圧周波数特性より、低周波数域での外乱抑圧が十分ではない。
・外乱抑圧ステップ応答から、ステップ状の外乱が入った場合、時間が経過してもその影響が残る。
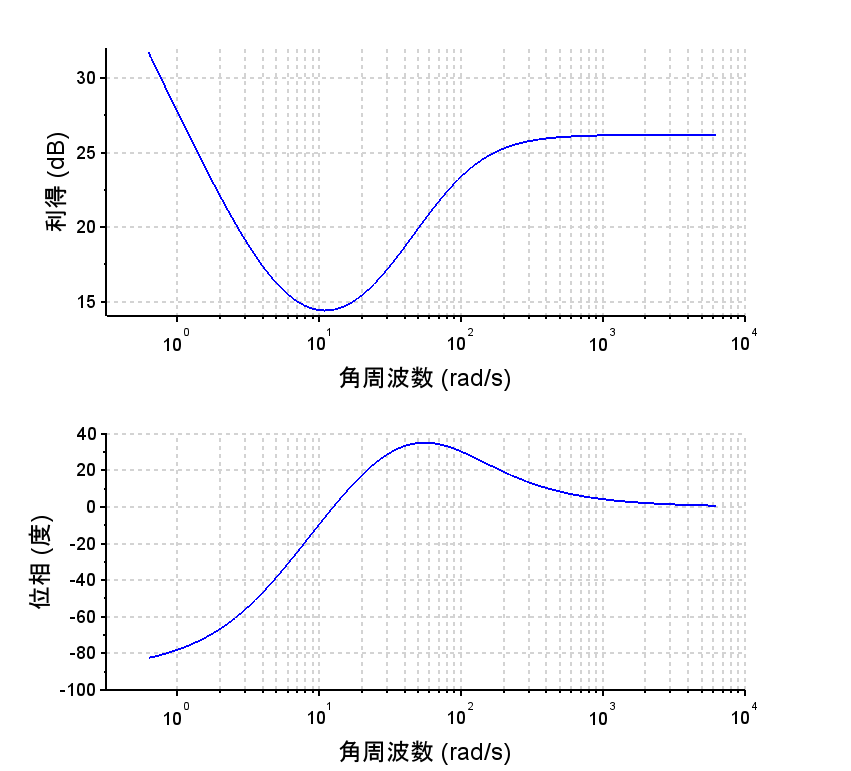
(位相進み補償+積分補償)
(位相進み補償+積分補償)
(位相進み補償+積分補償)
(位相進み補償+積分補償)
(位相進み補償+積分補償)
(位相進み補償+積分補償)
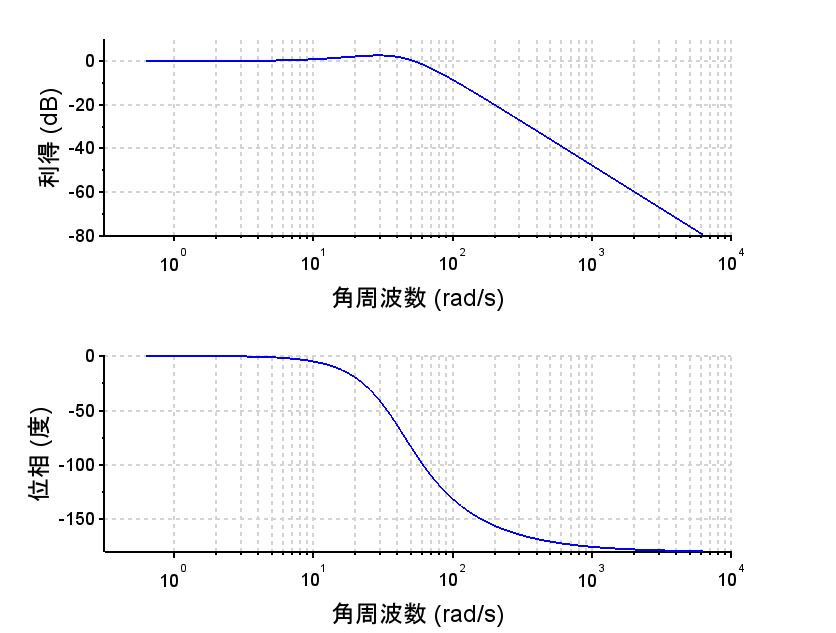
*位相進み補償+積分補償の場合
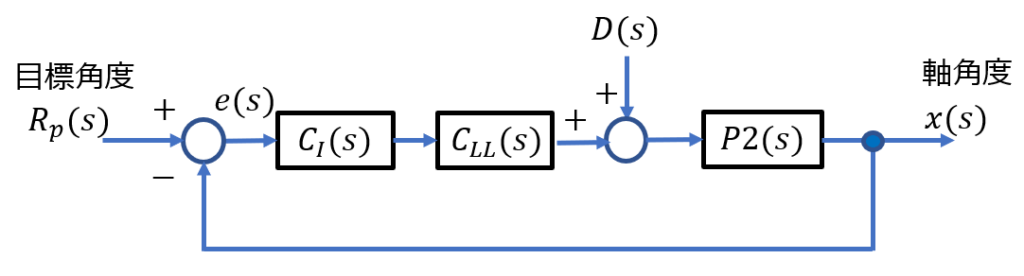
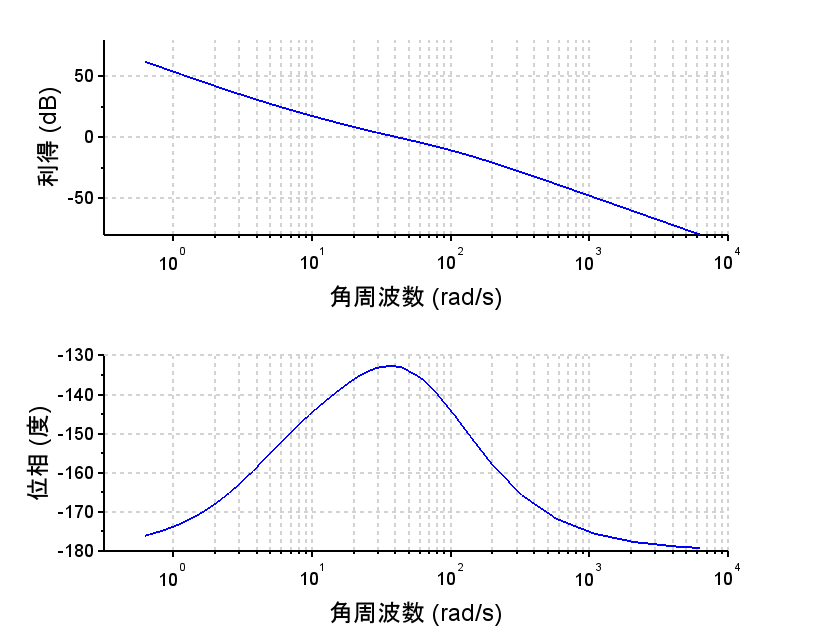
位相進み補償:$$C_{LL} (s) = K_p \frac{ 1+saT}{1+sT}$$積分補償:$$C_I (s)=\frac{s+ \frac{1}{T_I }}{s}$$ ※目標値応答特性$$T(s)=\frac{x(s)}{R_\omega (s)}=\frac{L(s)}{1+L(s)}$$ $$L(s)=K_p \frac{1+saT}{1+sT}\frac{s+\frac{1}{T_I }}{s}\frac{K}{s(\tau_1 s+1)}$$ $$=\frac{K_p K\left(s+\frac{1}{T_I }\right)(1+saT)}{s^2 (1+sT)(\tau_1 s+1)}$$ ※外乱抑圧特性 $$\frac{x(s)}{D (s)} = \frac{P2(s)}{1+L (s)}$$
制御器設計値:\(K_p=1.2, T=0.01, a=17, T_I=0.05\)
また、ゲイン交差周波数は40[rad/s]とする。
・開ループ伝達関数が2型のため定常位置偏差、定常速度偏差は0となる。
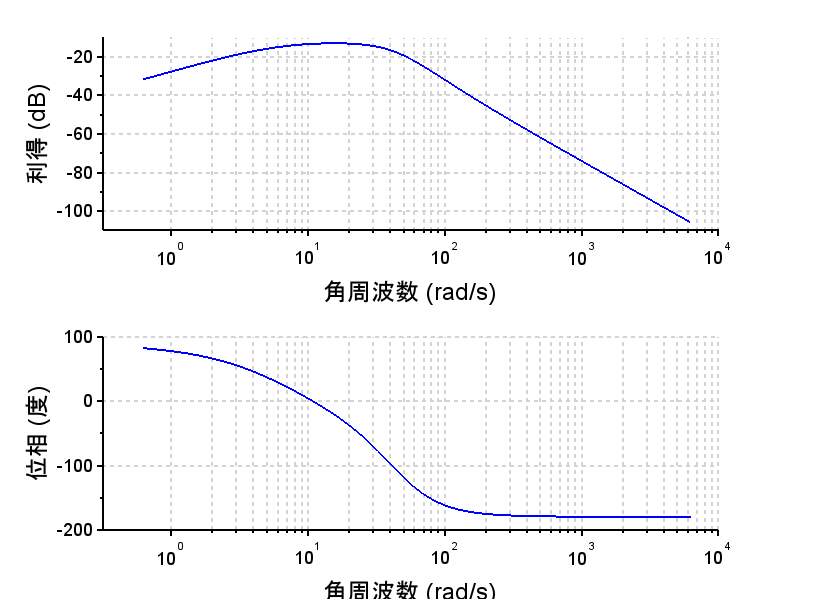
・位相進み+積分補償器の周波数特性より、低域でのゲインは\(\frac{1}{s}特性(-20dB/dec)で上がっていることが分かる。これにより位相特性が劣化するが、位相進み補償器により、10から300[rad/s]近傍における位相を改善している。これは、過渡応答での減衰特性の改善に寄与する。
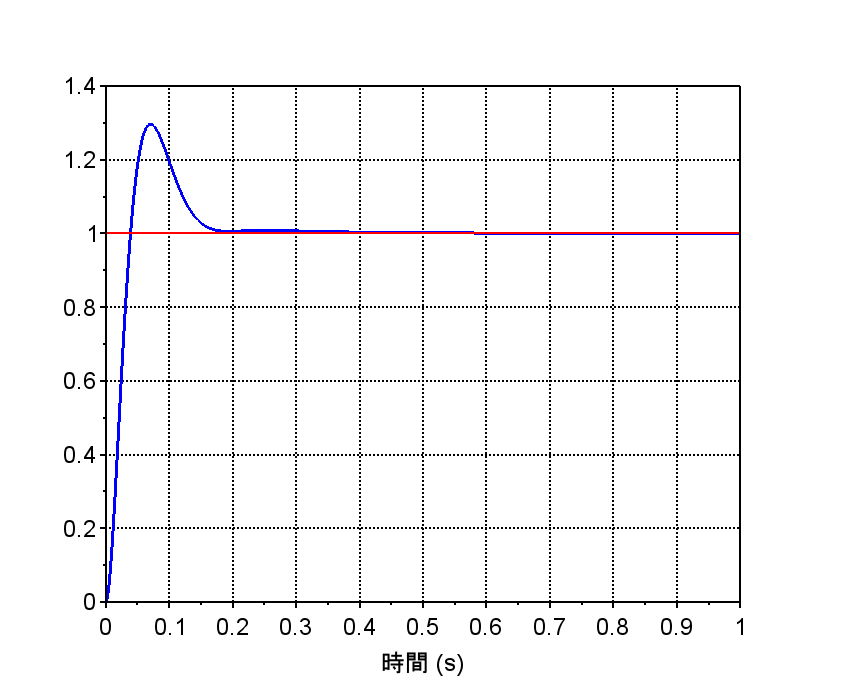
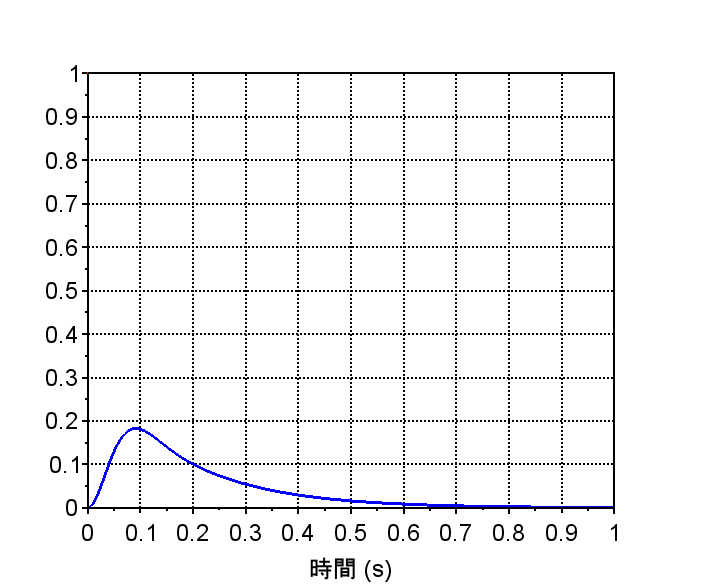
・外乱抑圧ステップ応答より、外乱がステップ状に入った場合、時間の経過とともに外乱の影響を0にできている。
モータ軸の角速度・角度検出方法
モータの速度制御/位置制御を行うためには、フィードバック信号の検出として角速度センサや角度センサを取り付ける必要がある。
※角速度センサ
*タコジェネレータ:フレミングの右手の法則を原理とする直流発電機。回転速度に比例した直流電圧を発生する。タコ(tacho)とは「速度」を意味するギリシャ語に由来。
※角度センサ
*回転ポテンショメータ:内部の抵抗体の分圧比によって角度検出を行う角度センサ
*インクリメンタルエンコーダ:ある位置から次の位置までの移動量を検知するタイプのエンコーダー
*アブソリュートエンコーダ:原点からどれくらい離れた位置にいるかを検知するタイプのエンコーダー
・光学式、磁気式など様々な方式がある。
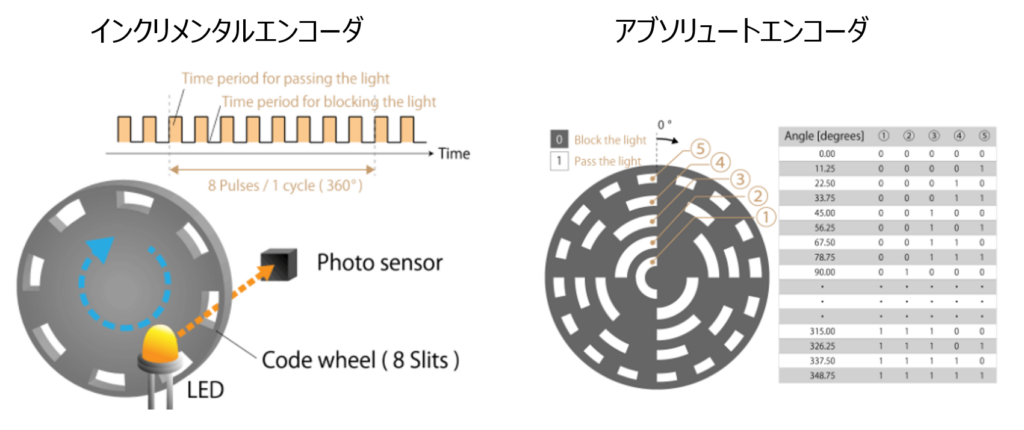
エンコーダに関する解説は、下記のサイトに詳しい。
https://www.akm.com/jp/ja/products/rotation-angle-sensor/tutorial/type-mechanism-2/

