7. 離散時間システムの定常特性

パルス伝達関数と定常偏差

離散時間系の定常偏差の考え方は、基本的に連続系における定常偏差の考え方と同様で、「内部モデル原理」で考えて良い。

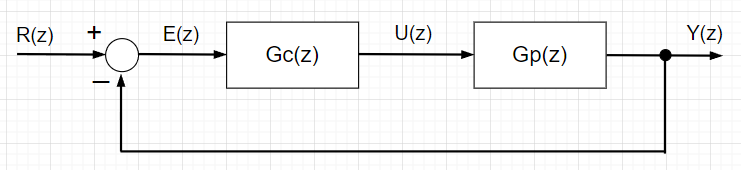
離散時間単位フィードバック制御系の図で、\(G_c(z)\)を制御器の伝達関数、\(G_p(z)\)を制御対象の伝達関数として、開ループ伝達関数を$$L(z)=G_c(z)G_p(z)$$とすると、偏差\(E(z)\)は、$$E(z)=\frac{1}{1 + L(z)}R(z)$$となる。この\(E(z)\)を逆Z変換すると、時間領域での偏差\(e(k)\)が求まる。また、最終値定理を使うことにより、\(k \rightarrow \infty\)における偏差（定常偏差）は$$e(\infty)=\lim_{k \rightarrow \infty} e(k)= \lim_{z \rightarrow 1}(1 - z^{-1})E(z)$$で求まる。

※（\(1 - z^{-1}\)）は連続時間系の\(s\)（微分要素）に相当する。

定常位置偏差

位置偏差を求めるので、目標値がステップ関数の場合を考える。目標値\( r(k)=I(k)\)なので、これをZ変換して、$$R(z) = \frac{z}{z-1} = \frac{1}{1 - z^{-1}}$$となる。従って、定常位置偏差は最終値定理より、$$e(\infty)=\lim_{k \rightarrow \infty} e(k) = \lim_{z \rightarrow 1}(1 - z^{-1})E(z)$$ $$=\lim_{z \rightarrow 1} (1 - z^{-1}) \frac{1}{1 + L(z)} \frac{1}{1- z^{-1}}$$ $$= \lim_{z \rightarrow 1} \frac{1}{1 + L(z)} = \frac{1}{1 + K_p}$$ 位置偏差定数（DCゲイン）$$K_p = \lim_{z \rightarrow 1} L(z)$$となる。
この式から内部モデル原理で考えて、\(L(z)\)が\(z=1\)に極を持てば、すなわち\(L(1)=\infty\)となるので定常位置偏差が\(０\)にできることが分かる。

定常速度偏差

速度偏差なので目標値はランプ関数の場合を考える。ランプ関数をZ変換して、$$R(z) = \frac{Tz}{(z -1)^2} = \frac{Tz^{-1}}{(1 - z^{-1})^2}$$となる。従って、定常速度偏差は最終値定理より、$$e(\infty) = \lim_{k \rightarrow \infty} e(k) = \lim_{z \rightarrow 1}(1 - z^{-1})E(z)$$ $$=\lim_{z \rightarrow 1} (1 - z^{-1})\frac{1}{1 + L(z)} \frac{Tz^{-1}}{(1 - z^{-1})^2} = \lim_{z \rightarrow 1} \frac{Tz^{-1}}{(1 - z^{-1})L(z)}$$ $$=\lim_{z \rightarrow 1} \frac{T}{(z -1)L(z)} = \frac{1}{K_v}$$ 速度偏差定数　$$K_v = \frac{1}{T} \lim_{z \rightarrow 1} ( z -1)L(z)$$となる。
この式から、\(L(z)\)が\(z=1\)に単極を持てば、\((z-1)\)が相殺されて\(K_v\)は有限な値となり、定常速度偏差は有限値となることが分かる。

定常加速度偏差

加速度偏差なので目標値はパラボラ関数（連続時間系では\(f(t)=t^2\)）の場合を考える。パラボラ関数のＺ変換は、$$R(z)=\frac{z(z+1)T^2}{2(z-1)^3}$$である。従って、定常加速度偏差は最終値定理より、$$e(\infty) = \lim_{k \rightarrow \infty} e(k) = \lim_{z \rightarrow 1}(1 - z^{-1})E(z)$$ $$=\lim_{z \rightarrow 1} (1 - z^{-1})\frac{1}{1 + L(z)}\frac{z(z+1)T^2}{2(z-1)^3} = \lim_{z \rightarrow 1}\frac{(z+1)T^2}{2(z-1)^2\left[1 + L(z)\right]}$$ $$=\lim_{z \rightarrow 1}\frac{T^2}{(z-1)^2L(z)} = \frac{1}{K_a}$$ 加速度偏差定数　$$K_a = \frac{1}{T^2}\lim_{z \rightarrow 1} (z-1)^2L(z)$$となる。
定常加速度偏差を有限値、もしくは\(0\)にするのは、一自由度制御系では困難であり、二自由度制御系など他の制御手法を考える必要がある。