8. 離散時間システムの安定性
tctyamインパルス応答が時間の経過とともに零に収束すれば、線形システムは安定である。離散時間システムのパルス伝達関数は、$$G(z) = \frac{b_0 z^m + b_1 z^{m-1} + \cdots + b_m}{z^n + a_1 z^{n-1} + \cdots + a_n} \;\;\;\; (n \ge m)$$である。この伝達関数の特性方程式（分母多項式=0）は、$$z^n + a_1 z^{n-1} + \cdots + a_n = 0$$である。この方程式の根、すなわち特性根【\(G(z)\)の極】を \(\lambda_1 , \lambda_2 , \cdots , \lambda_n\) として、すべて相異なるとすると\(G(z)\)は部分分数展開でき、入力を\(U(z)\)として、出力\(Y(z)\)は、$$Y(z) = G(z)U(z) = \sum_{i=1}^{n} \frac{c_i z}{z - \lambda_i}U(z)$$となる。\(c_i\)は部分分数展開したときの係数。
ここで、$$\frac{z}{z - \lambda_i} =\sum_{l=0}^{\infty} \lambda_{i}^{l} z^{-l} = 1 + \lambda_i z^{-1} + \lambda_{i}^{2} z^{-2} + \lambda_{i}^{3} z^{-3} + \cdots $$となるので、出力\(y(k)\)は\(Y(z)\)を逆Z変換して、$$y(k) = \sum_{i=1}^{n} c_i \sum_{l=0}^{\infty} \lambda_{i}^{l} u(k - l)$$ と表せる。
入力\(u(k)\)をインパルスとすると、$$u(k) = \begin{cases} 0 \;\;\;\; (k \neq 0) \\ 1 \;\;\;\; (k = 0) \end{cases}$$なので、$$y(k) = \sum_{i=1}^{n} c_i \lambda_{i}^{k} = c_1 \lambda_{1}^{k} + c_2 \lambda_{2}^{k} + \cdots + c_n \lambda_{n}^{k}$$ となる。インパルス応答が時間の経過とともに零に収束すれば線形システムは安定なので、\(k \rightarrow \infty \)で \(y(k) \rightarrow 0\) になればよい。そのためには、$$\left|\lambda_i\right| \lt 1 \;\;\;\; (\forall i)$$ が必要十分条件となる。すなわち、特性根（伝達関数\(G(z)\)の極）の絶対値が複素平面の単位円内にあれば離散時間システムは安定ということになる。これは、連続時間システムで伝達関数\(G(s)\)の極が複素平面の左半平面にあればシステムが安定ということに相当する。
Scilabでの安定判別
Scilabを使用して離散時間システムの安定性を判別するには、
１）離散時間システムの伝達関数を定義する。
２）roots関数を使用して伝達関数の分母多項式の根を求める。
３）求めた極の絶対値を計算する。
４）全ての極の絶対値が1以下であることを確認する。
これにより、離散時間システムの安定判別ができる。
//離散時間システムの安定判別
z=%z;
//伝達関数の定義
Gz=(z+1)/(z^2-0.7*z+0.3);
//システム関数に変換
Gzz=syslin('d', Gz);
//分母の根を求める
p=roots(Gzz.den);
//根の絶対値を求める
abs_p=abs(p);
//全ての根が１未満ならTrueを返す
stable=and(abs_p <1);
極とインパルス応答
連続時間系での極とインパルス応答の関係は、こちらの図にあるように、極が複素平面の左半平面に有れば安定であり、虚軸から遠いほど速く収束する。また、複素極であればインパルス応答は振動的になる。
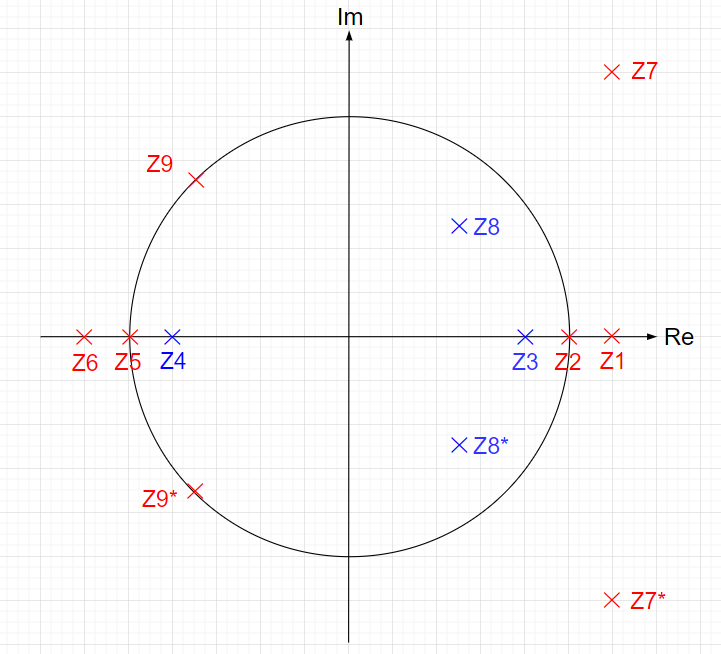
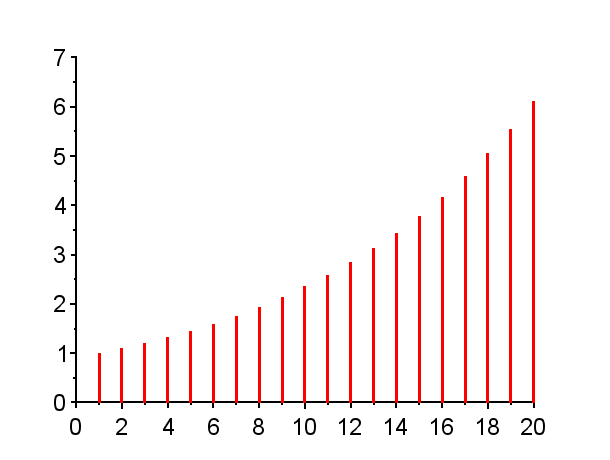
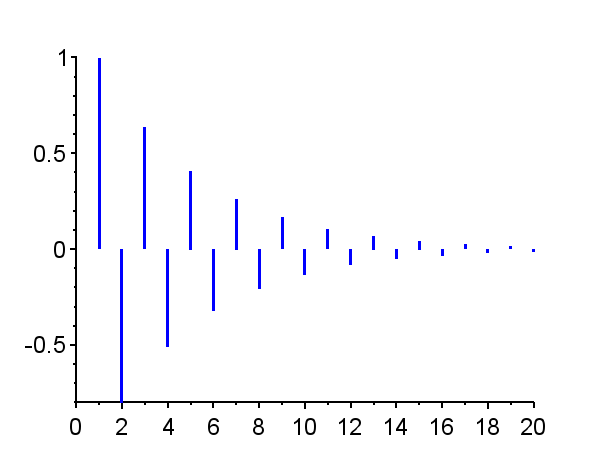
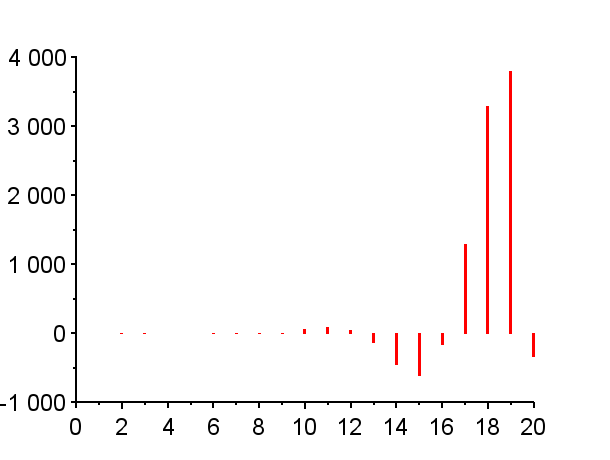
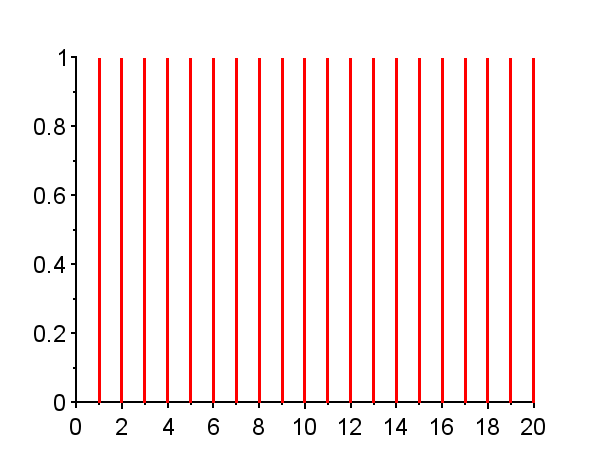
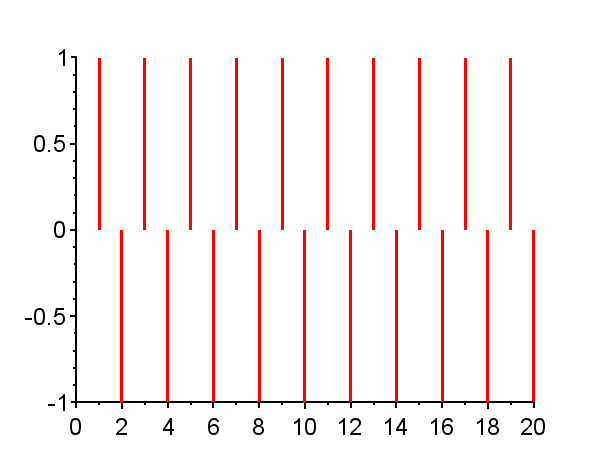
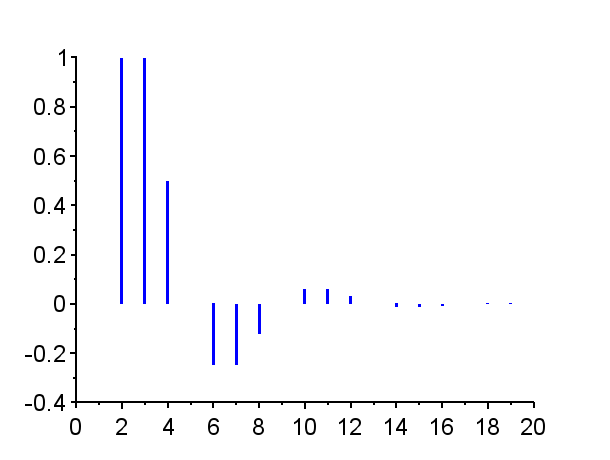
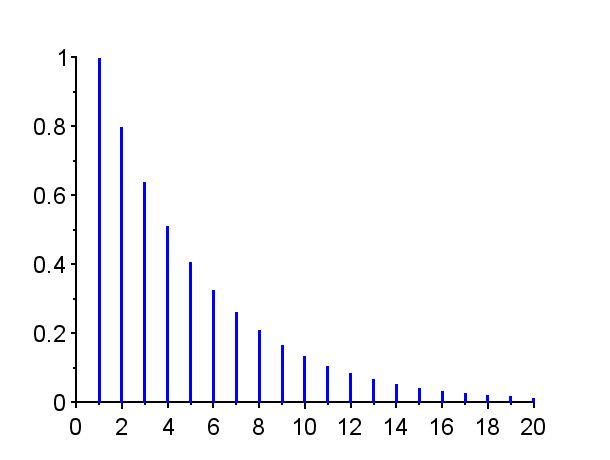
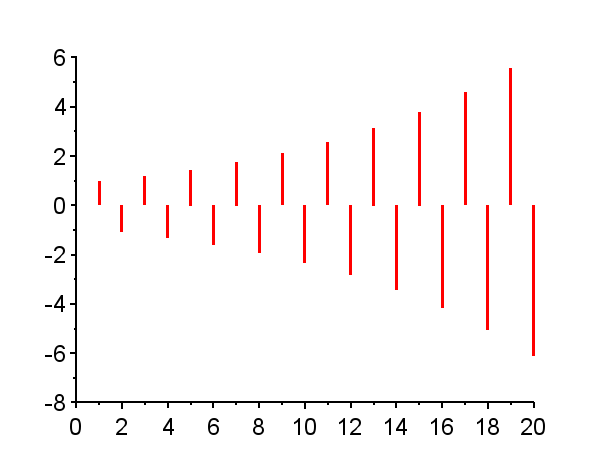
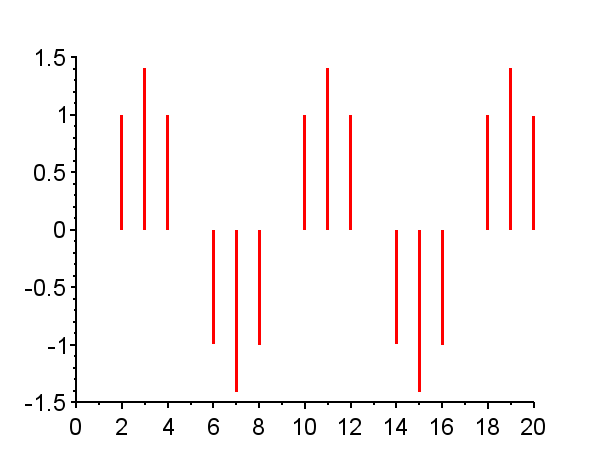
※「赤」で記した極は不安定極である。（単位円上の極は安定限界であるが、実用的には一般的に不安定である。）「青」で記した極は安定極である。極の配置によりインパルス応答の振る舞いは異なる。
離散時間系での極とインパルス応答の関係は、見た目がやや複雑であるが、安定性の必要十分条件は、極が単位円内にある場合その系は安定であり、インパルス応答は有限の値に収束する。
極が単位円外にある場合{Z1},{Z6},{Z7,Z7*}その系は不安定であり、インパルス応答は発散する。発散の仕方は、極が実軸上にある場合{Z1},{Z6}と、極が複素極である場合{Z7,Z7*}で、異なった振る舞いとなる。
極が単位円内で複素平面の右半平面に有る場合{Z3},{Z4},{Z8,Z8*}では、連続時間系で安定なシステムのインパルス応答に近い振る舞いを示す。すなわち、極が実軸上にある場合{Z3}はインパル応答は減衰指数関数的な挙動を示し、極が複素極の場合{Z8,Z8*}はインパル応答は減衰振動的な挙動となる。
また、極が単位円上にある場合{Z2}{Z5}{Z9,Z9*}で、極が１の場合{Z2}では、そのインパルス応答は、連続時間系において原点に極がある場合のインパルス応答のような振る舞いを示す。極が\(-1\)の場合{Z5}では、そのインパル応答は０と１を繰り返す振動となる。極が単位円上で左半平面の複素極の場合{Z9,Z9*}では、そのインパル応答は定常振動となる。
双一次変換による安定判別
一次関数 $$w=\frac{z-1}{z+1}$$による写像を双一次変換という。これは\(z\)平面を\(w\)平面に写像することになり、\(z\)平面の複素平面の単位円内を\(w\)領域の複素平面の左半平面に写像することになる。\(w\)平面は連続時間系の\(s\)平面とは異なるが、\(z\)平面の単位円内（極の安定な領域）を複素平面の左半平面に写像するので、連続時間系の安定判別法が利用できる。（\(z\)平面、\(w\)平面、\(s\)平面ともに複素平面であるが、各平面上の点は異なる点に写像されることになる。）
\(z=e^{j\theta}\)とすると、\(|z|=1\)で単位円となる。このとき、$$w=\frac{e^{j\theta}-1}{e^{j\theta}+1}=\frac{\cos \theta + j\sin \theta - 1}{\cos \theta + j\sin \theta +1} $$ $$= \frac{ \{(\cos \theta - 1 ) + j\sin \theta\}\{(\cos \theta +1) -j\sin \theta\}}{\{(\cos \theta +1) + j\sin \theta\}\{(\cos \theta + 1) - j\sin \theta \}}$$ $$=\frac{\cos^2 \theta -1 + \sin^2 \theta + j2\sin \theta}{(\cos \theta +1)^2 + \sin^2 \theta} = \frac{j 2 \sin \theta}{2 + 2 \cos \theta} =j \frac{\sin \theta}{1 + \cos \theta}$$となる。従って、\(w\)は純虚数となる。\(z=e^{j\theta}\)の\(\theta\)を\(-\pi \sim +\pi\)変化させると、すなわち単位円周上を一周変化させると、\(w\)は虚軸上を\(-j\infty \sim +j\infty\)変化することになる。つまり、\(z\)平面の単位円周上が\(w\)平面の虚軸に写像される。また、\(w\)平面の左半平面が\(z\)平面の単位円内に写像されることになる。従って、\(z\)の特性方程式で、\(z=\frac{1+w}{1-w}\)と置き換えて\(w\)の多項式に変換すれば、ラウスの安定判別が使えることになる。
双一次変換による安定判別【例】
特性方程式が、\(z^2 + az + b = 0\)のとき、\(z = \frac{1 +w }{1 - w}\)とすると、$$\left(\frac{1+w}{1-w}\right)^2 + a\left(\frac{1+w}{1-w}\right) + b = 0$$ $$(1 - a + b)w^2 + 2(1 - b)w + 1+ a+b =0$$各係数が正であれば、根の実部が負となることから、$$ 1 - a + b \gt 0 , \;\;\; 1 - b \gt 0 , \;\;\; 1 + a+ b \gt 0$$
$$G(z)=\frac{z+1}{z^2-0.7z+0.3}$$とすると、特性方程式は、\(z^2 - 0.7z +0.3 =0\)で、\(a=-0.7, b=0.3\)なので、\(1-a+b=2 \gt 0\)、\(1-b=0.7 \gt 0\)、\(1+a+b=0.6 \gt 0\)となり、安定と判別できる。 特性方程式\(z^2 - 0.7z +0.3 =0\)の根を求めると\(p=0.35 \pm 0.421j \) となり、根は\(z\)平面の単位円内にあるので、安定である。
“8. 離散時間システムの安定性” に対して1件のコメントがあります。
コメントは受け付けていません。