10. システムの正準形と等価変換
等価変換
離散時間システムの状態方程式、出力方程式を$$x(k+1)=Ax(k) + bu(k) \\ y(k)=cx(k) \;\;\;\; \;\;\;\;\; \cdots \cdots (1)$$とする。ある正則行列\(P \;\;\;(n \times n)\)(逆行列が存在する行列)を使って状態変数\(x(k)\)を\(x = P \tilde{x}\)と変換する。(\(\tilde{x} = P^{-1}x\))このとき状態方程式は、$$\tilde{x}(k+1) = P^{-1}x(k+1) = P^{-1}\{A x(k) + b u(k)\}$$ $$= P^{-1}AP \tilde{x}(k) + P^{-1} b u(k)$$ $$y(k) = c P\tilde{x}(k)$$となる。ここで、\(\tilde{A} = P^{-1}AP \;\;\; \tilde{b} = P^{-1} b \;\;\; \tilde{c} = c P\)とすると、$$\tilde{x}(k+1) = \tilde{A} \tilde{x} (k) + \tilde{b} u(k) \\ y(k) = \tilde{c} \tilde{x}(k) \;\;\;\;\;\;\;\;\; \cdots \cdots (2)$$となる。\(u(k)\)は入力、\(y(k)\)は出力で変わらないので入出力関係は不変である。従って、元の状態方程式、出力方程式で表されたシステム \((1)\)式と変換後のシステム \((2)\)式は等価なシステムである。また、この変換を等価変換という。
※入出力関係が不変で等価なシステムではあるが、内部構造は変わることになる。すなわちシステムを実装する場合は、内部構造を構成する各要素の動作(アンプの飽和などの非線形な振る舞いを含む)は異なることに注意する必要がある。等価変換を解析の見通しを良くする手法と考えればよい。
等価なシステムの伝達関数
\((2)\)式から伝達関数を求めると、$$\tilde{G}(z) = \tilde{c} (zI - \tilde{A})^{-1} \tilde{b}$$となる。この伝達関数に\(\tilde{A} = P^{-1}AP \;\;\; \tilde{b} = P^{-1} b \;\;\; \tilde{c} = c P\)を代入すると、$$\tilde{G}(z) = c P(zI - P^{-1}AP)^{-1} P^{-1} b = cP\{P^{-1} (zI - A)P\}^{-1} P^{-1} b = c(zI - A)^{-1} b = G(z)$$となる。これから、等価変換しても伝達関数は同じであることが分かる。状態方程式、出力方程式を等価変換しても伝達関数は同一となることは、入出力関係が不変であることからも当然である。ただし、状態方程式、出力方程式から伝達関数は一意に決まるが、伝達関数から状態方程式、出力方程式は一意に定まらない。つまり、入出力関係が同一でも様々なシステムが作れることが推測できる。
対角正準形
システム行列\(A \;\;\; (n \times n)\)について、$$|zI - A| = z^n + a_n z^{n-1} + a_{n-1} z^{n-2} + \cdots + a_2 z + a_1 = 0$$が特性方程式で、これを満たす\(n\)個の根 \(z = \lambda_1 , \lambda_2 , \cdots , \lambda_n\) を\(A\)の固有値という。ここで全ての固有値は相異なるとする。固有値\(\lambda_i\)に対応する固有ベクトルを\(v_i\)とすると$$\lambda_i v_i = A v_i \;\;\;\;\;\; (i=1,2, \cdots, n) $$が成り立つ。固有ベクトルは一次独立なので、これを並べて$$T= \begin{bmatrix} v_1 & v_2 & \cdots & v_n \end{bmatrix}$$と定義すれば、\(T\)は正則となる(つまり\(T^{-1}\)が存在する。)。
行列の対角化
与えられた正方行列 \(A\) に対して,正則行列\(P\)をうまく取ってきて\(P^{-1}AP\)を対角行列にする操作を対角化と言う。
証明などは、こちらへ
\(A\)と\(T\)の積は、$$AT = A \begin{bmatrix} v_1 & v_2 & \cdots & v_n \end{bmatrix} = \begin{bmatrix} \lambda_1 v_1 & \lambda_2 v_2 & \cdots & \lambda_n v_n \end{bmatrix}$$ $$ = \begin{bmatrix} v_1 & v_2 & \cdots & v_n \end{bmatrix} \begin{bmatrix} \lambda_1 & & & \\ & \lambda_2 & & \\ & & \ddots & \\ & & & \lambda_n \end{bmatrix} = T \Lambda$$となる。 \(\Lambda = \begin{bmatrix} \lambda_1 & & & \\ & \lambda_2 & & \\ & & \ddots & \\ & & & \lambda_n \end{bmatrix} \)は固有値を要素とする対角行列である。\(AT = T \Lambda\)なので、$$\Lambda = T^{-1} A T$$となり、システム行列\(A\)を固有値を要素とした対角行列に変換できる。これを対角変換といい、\(T\)を対角変換行列という。
※固有値に重複するものがある(重根がある)場合、この方法では対角変換できない。その場合は、ジョルダン正準形に変換する。ジョルダン正準形に関しては、こちらを参考にして欲しい。
対角正準形のシステム構成
\((1)\)式のシステムを対角変換行列\(T\)を使って等価変換すれば、$$\tilde{x}(k+1) = \Lambda \tilde{x}(k) + \beta u(k) \\ y(k) = \gamma \tilde{x}(k)$$ $$\Lambda = \begin{bmatrix} \lambda_1 & & & \\ & \lambda_2 & & \\ & & \ddots & \\ & & & \lambda_n \end{bmatrix} $$ $$\beta = T^{-1}b \;\;\;\; \gamma = cT$$ となる。
これより、状態変数線図は「対角正準形の状態変数線図」のように表せる。
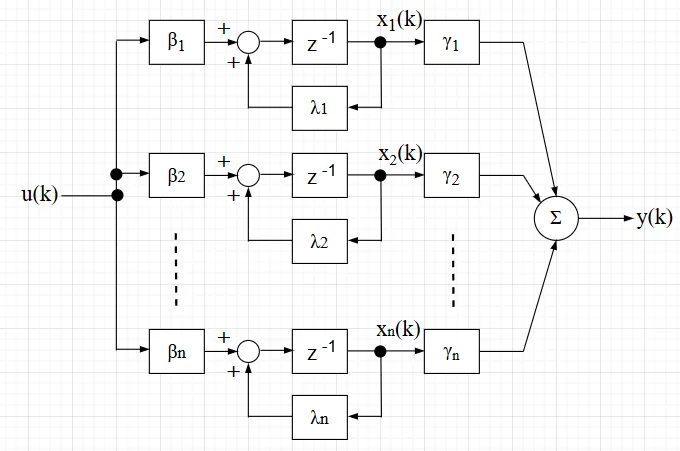
対角正準形の可制御性・可観測性
「対角正準形の状態変数線図」から分かるように、可制御のためには、入力\(u(k)\)が各状態変数 \(x_1(k),x_2(k), \cdots , x_n(k)\)の全てに影響しないといけないので、\(\beta_1 , \beta_2, \cdots, \beta_n\)が全て非零でなければならない。また、可観測のためには、出力\(y(k)\)が全ての状態変数 \(x_1(k),x_2(k), \cdots , x_n(k)\)から定まらないといけないので、\(\gamma_1, \gamma_2, \cdots , \gamma_n\)が全て非零でなければならない。まとめると
可制御条件:\(\beta_i \ne 0 \;\;\;\; i=1,2,\cdots, n\)
可観測条件:\(\gamma_i \ne 0 \;\;\;\; i=1,2,\cdots, n \)
となる。
ジョルダン正準形のシステム構成と可制御性・可観測性【例】
固有値\(\lambda_i\)に重根がある場合、単純に対角化はできずジョルダン正準形に変換することになる。例えば、\(\lambda_1\)は単根、\(\lambda_2\)は2重根とすると次のジョルダン正準形で表せる。$$x(k+1) = \begin{bmatrix} \lambda_1 & & \\ & \lambda_2 & 1 \\ & & \lambda_2 \end{bmatrix} x(k) + \begin{bmatrix} \beta_1 \\ \beta_2 \\ \beta_3 \end{bmatrix} u(k) $$ $$y(k) = \begin{bmatrix} \gamma_1 & \gamma_2 & \gamma_3 \end{bmatrix} x(k)$$この状態方程式、出力方程式を状態変数線図で表すと「ジョルダン正準形の状態変数線図」となる。
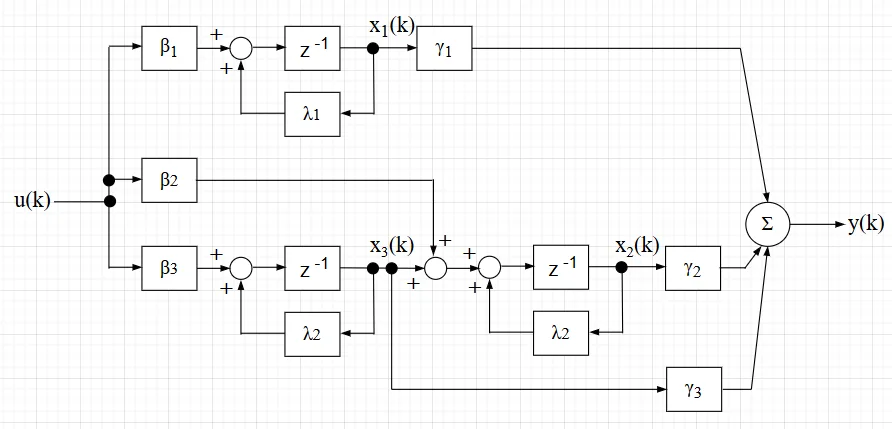
「ジョルダン正準形の状態変数線図」から分かるように、可制御のためには、入力\(u(k)\)が各状態変数 \(x_1(k),x_2(k) , x_3(k)\)に影響しないといけないが、\(\beta_2 = 0\)であっても、\(x_2(k)\)は\(x_3(k)\)を通じて\(u(k)\)の影響を受けるので可制御性は保たれる。従って、可制御を満たす条件は、\(\beta_1\ne 0 , \;\; \beta_3\ne 0\)となる。また、可観測のためには、出力\(y(k)\)が状態変数 \(x_1(k),x_2(k), x_3(k)\)から定まらないといけないが、\(\gamma_3 = 0\)であっても、\(x_3(k)\)は\(x_2(k)\)を通じて出力\(y(k)\)に現れるので可観測性は保たれる。従って、可観測を満たす条件は、\(\gamma_1\ne 0 , \;\; \gamma_2 \ne 0\)となる。

