11. 可制御正準形と可観測正準形
可制御正準形
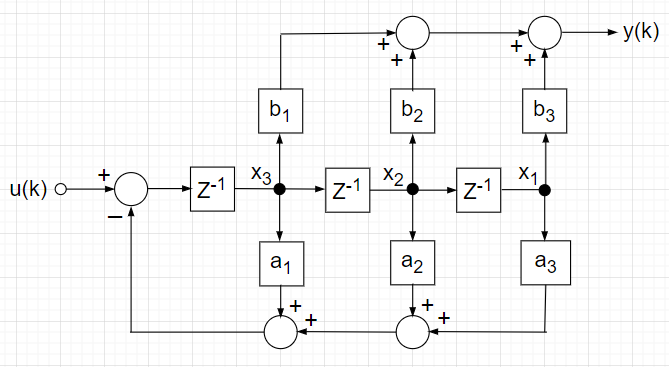
可制御正準形とは、状態空間表現を用いたシステムのうち、制御入力によって任意の状態に達することができる最も単純な形式の一つである。可制御正準形では、制御入力がシステムの全ての状態変数に対して影響を与えることができるため、制御系の設計が容易になる。このため可制御正準形はシステムの極の設定や最適制御を求める際に用いられることが多い。
「可制御正準形の状態変数線図【例】」を基に、図中のように状態変数を\(x_1, x_2, x_3\)として、状態方程式と出力方程式を書くと、$$\begin{bmatrix} x_1(k+1) \\ x_2(k+1) \\ x_3(k+1) \end{bmatrix} = \begin{bmatrix}0 & 1 & 0 \\ 0 & 0 & 1 \\ -a_3 & -a_2 & -a_1 \end{bmatrix} \begin{bmatrix} x_1(k) \\ x_2(k) \\ x_3(k) \end{bmatrix} + \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix} u(k)$$ $$y(k) = \begin{bmatrix} b_3 & b_2 & b_1 \end{bmatrix} \begin{bmatrix} x_1(k) \\ x_2(k) \\ x_3(k) \end{bmatrix} $$となる。構造の特徴として、すべての状態変数\(x_1,x_2,x_3\)が入力端にフィードバックされている。
Z領域で整理して伝達関数を求める。$$E(z)=U(z) - \{a_1 X_3(z) + a_2 X_2(z) + a_3 X_1(z)\} $$ $$X_3(z) = E(z) z^{-1} ,\;\; X_2(z) = E(z) z^{-2} ,\;\; X_1(z)= E(z) z^{-3}$$整理すると$$U(z) = E(z)(1 + a_1 z^{-1} + a_2 z^{-2} + a_3 z^{-3} ) $$となる。また、$$Y(z) = b_1 X_3(z) + b_2 X_2(z) + b_3 X_1(z) = E(z) (b_1 z^{-1} + b_2 z^{-2} + b_3 z^{-3}) $$である。 以上より、$$G(z) = \frac{Y(z)}{U(z)} = \frac{E(z) (b_1 z^{-1} + b_2 z^{-2} + b_3 z^{-3}) }{E(z)(1 + a_1 z^{-1} + a_2 z^{-2} + a_3 z^{-3} )} = \frac{ b_1 z^{-1} + b_2 z^{-2} + b_3 z^{-3}}{1 + a_1 z^{-1} + a_2 z^{-2} + a_3 z^{-3} }$$と伝達関数が求まる。
可観測正準形
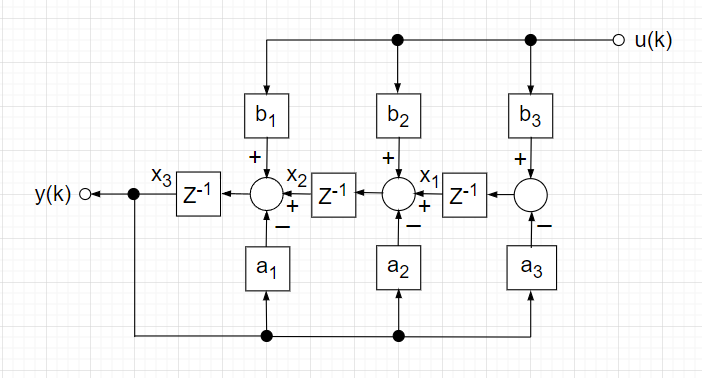
可観測正準形とは、制御理論における状態空間表現の一つで、出力ベクトル \(y(k)\) が状態変数ベクトル\(x(k)\) の線形結合として表されるため、システムの状態を出力から推定することができる。この性質から、可観測正準形はシステムの観測可能性を分析することや状態観測器の設計などに利用される。
「可観測正準形の状態変数線図【例】」を基に状態方程式と出力方程式を書くと、$$\begin{bmatrix} x_1(k+1) \\ x_2(k+1) \\ x_3(k+1) \end{bmatrix} = \begin{bmatrix}0 & 0 & -a_3 \\ 1 & 0 & -a_2 \\ 0 & 1 & -a_1 \end{bmatrix} \begin{bmatrix} x_1(k) \\ x_2(k) \\ x_3(k) \end{bmatrix} + \begin{bmatrix} b_3 \\ b_2 \\ b_1 \end{bmatrix} u(k)$$ $$y(k) = \begin{bmatrix} 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x_1(k) \\ x_2(k) \\ x_3(k) \end{bmatrix} $$となる。構造の特徴として、出力がすべて遅延素子\(z^{-1}\)にフィードバックされている。
Z領域で整理して伝達関数を求める。$$X_1(z) = \{b_3 U(z) - a_3 Y(z)\} z^{-1} $$ $$X_2(z) = \{X_1(z) + b_2 U(z) - a_2 Y(z)\} z^{-1}$$ $$X_3(z) = \{X_2(z) + b_1 U(z) - a_1 Y(z)\} z^{-1}$$ $$Y(z) = X_3(z) = b_1 U(z) z^{-1} - a_1 Y(z) z^{-1} + X_1(z) z^{-2} + b_2 U(z) z^{-2} - a_2 Y(z) z^{-2} $$ $$= b_1 U(z) z^{-1} - a_1 Y(z) z^{-1} + b_2 U(z) z^{-2} - a_2 Y(z) z^{-2} + b_3 U(z) z^{-3} - a_3 Y(z) z^{-3}$$整理すると、$$Y(z)\{ 1 + a_1 z^{-1} + a_2z^{-2} + a_3 z^{-3} \} = U(z) \{b_1 z^{-1} + b_2 z^{-2} + b_3 z^{-3} \}$$ 以上より、$$G(z) = \frac{Y(z)}{U(z)} = \frac {b_1 z^{-1} + b_2 z^{-2} + b_3 z^{-3} }{1 + a_1 z^{-1} + a_2z^{-2} + a_3 z^{-3}}$$と伝達関数が求まる。
以上のように、伝達関数が同一(入出力関係が同じ)であっても、可制御正準形、可観測正準形のように異なった状態方程式、出力方程式、状態変数線図で表現できる。解析、設計などそれぞれの用途に合わせて適切な構造に変換して使用する。


“11. 可制御正準形と可観測正準形” に対して1件のコメントがあります。
コメントは受け付けていません。