12. 状態フィードバック制御
離散時間系の状態フィードバックは、システムの状態変数を測定し、その情報を使用してシステムを制御する方法である。この方法は、システムの安定化や望ましい挙動(適切な極配置)を達成するために使用される。状態フィードバック制御では、システムの状態変数の測定値は、制御器内で処理され、制御信号(操作量)を生成する。制御信号は、制御装置からアクチュエーターに送信され、システムを制御することになる。
状態フィードバックシステムの構成
状態フィードバックシステムは、$$x(k+1) = Ax(k) + bu(k) \;\;\;\ y(k)=c x(k)$$ $$ u(k) = -f x(k) + v(k)$$ \(f =\begin{bmatrix} f_1 & f_2 & \cdots & f_n \end{bmatrix}\):状態フィードバックゲイン、\(v(k)\):外部入力
と表される。
式を整理すると、$$x(k+1) = (A - b f)x(k) + b v(k) \;\;\; y(k)= c x(k)$$となる。この状態変数線図は、「状態フィードバックシステム」のように表せる。
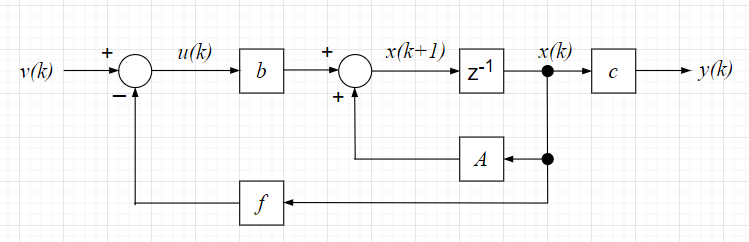
\((A,b)\)が可制御とすると、可制御正準形に変換でき、$$A = \begin{bmatrix} 0 & 1 & & \\ \vdots & & \ddots & \\ 0 & & & 1 \\ -a_n & -a_{n-1} & \cdots & -a_1 \end{bmatrix} , \;\;\;\; b = \begin{bmatrix} 0 \\ \vdots \\ 0 \\1 \end{bmatrix}$$ $$A - b f = \begin{bmatrix} 0 & 1 & & \\ \vdots & & \ddots & \\ 0 & & & 1 \\ -(a_n + f_1) & -(a_{n-1} + f_2) & \cdots & -(a_1 + f_n) \end{bmatrix}$$ となる。
状態フィードバックシステムの特性方程式
状態フィードバック閉ループ系の特性方程式は、$$\phi(z) = | z I -(A - b f)| $$ $$= z^n +(a_1 + f_n)z^{n-1} + \cdots + (a_{n-1} + f_2)z + a_n + f_1 = 0$$となる。 この特性方程式の根 (\(A-bf\)の固有値)が状態フィードバック閉ループ系の極であり、フィードバックゲイン\(f\)を調整することで、この極を自由に配置できることがわかる。なお、状態フィードバックによる零点は不変である。
極配置問題
状態フィードバック閉ループ系の特性方程式は、$$\phi(z) = | z I -(A - b f)| $$ $$= z^n +(a_1 + f_n)z^{n-1} + \cdots + (a_{n-1} + f_2)z + a_n + f_1 = 0$$であり、極(特性根)を\(\lambda_1, \lambda_2, \cdots ,\lambda_n\)となるように配置したとすると、特性方程式は、$$\phi(z) = (z - \lambda_1)(z - \lambda_2) \cdots (z - \lambda_n)$$ $$= z^n + \alpha_1 z^{n-1} + \cdots + \alpha_{n-1} z + \alpha_n = 0$$ となる。この2つの特性方程式の係数を比較すると、$$a_i + f_{n-i+1} = \alpha_i \;\;\;\; (i = 1,2,\cdots, n)$$である。よって、$$f = \begin{bmatrix} f_1 & f_2 & \cdots & f_n \end{bmatrix} = \begin{bmatrix} \alpha_n - a_n & \alpha_{n-1} -a_{n-1} & \cdots & \alpha_1 - a_1 \end{bmatrix}$$ このように、極配置を決めて、それに応じた状態フィードバックゲインを決定することができる。
Scilabによる状態フィードバックシステムの設計・解析【例】
$$x(k+1) = \begin{bmatrix} 1 & -1 \\ 2 & 0 \end{bmatrix} x(k) + \begin{bmatrix} 0 \\1 \end{bmatrix} u(k)$$ $$y(k) = \begin{bmatrix} -1 & 0 \end{bmatrix} x(k)$$の不安定なシステムにおいて、極を単位円内の実軸上の\(\{0.4 , 0.1 \}\)にするように状態フィードバックゲインを決定する。
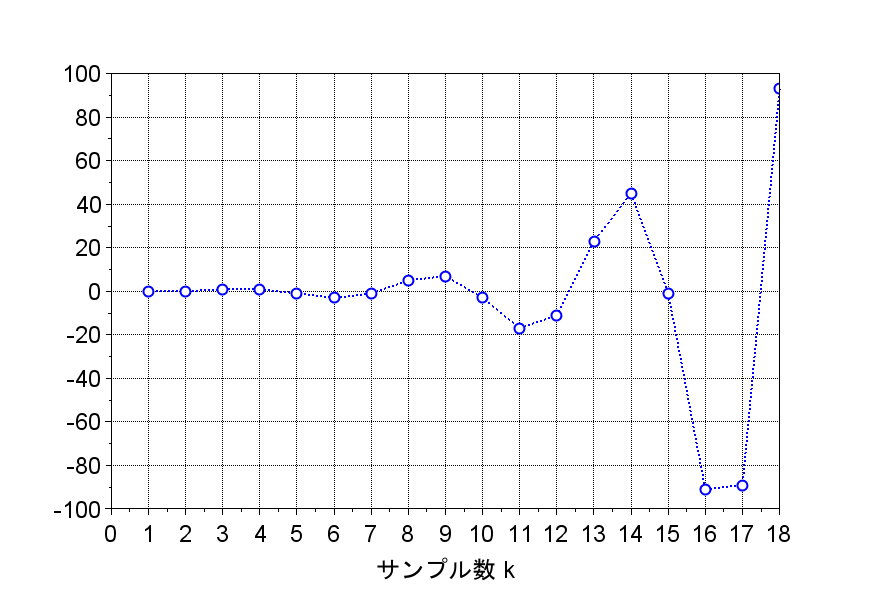
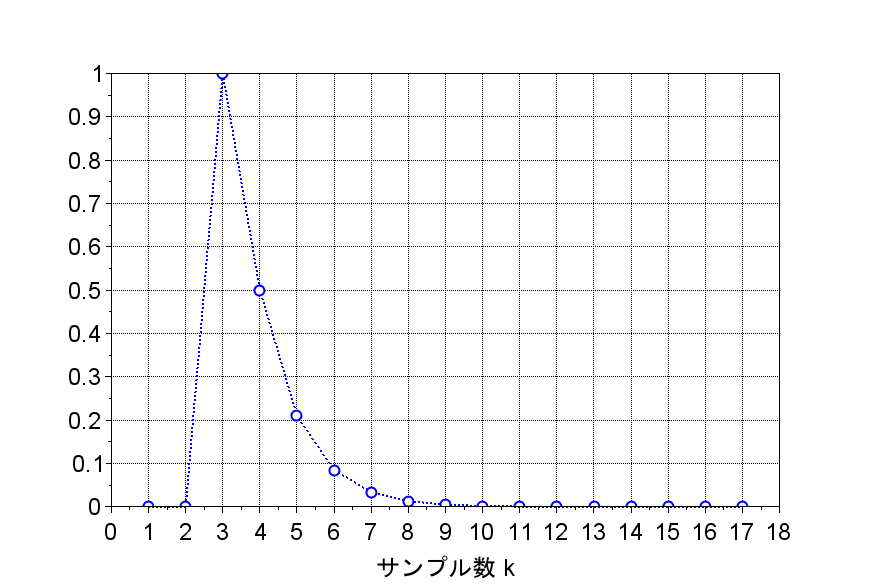
安定化したシステムのインパルス応答
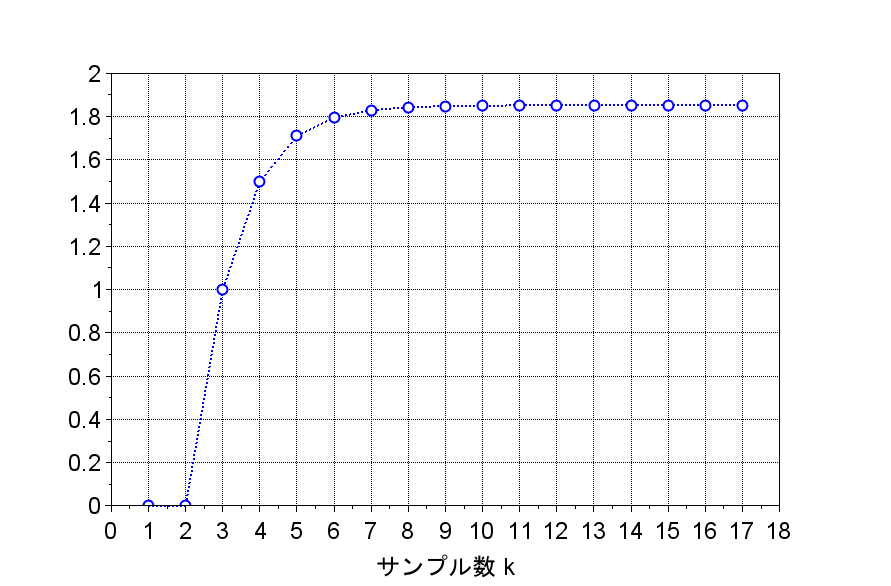
安定化したシステムのステップ応答
Scilab スクリプト
//状態フィードバックシステムの設計・解析
clear; clf;
z=%z; e=%e; i=%i;
//元システムの設定
A=[1 -1 ; 2 0]; b=[0 ; 1]; c=[-1 0];
Pz=syslin('d',A,b,c);
opoles=spec(A); /* 固有値の計算*/
Pzz=ss2tf(Pz);
//インパルス応答
u=[1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0];
y = flts(u,Pzz);
scf(0); plot(y,'-o');
//状態フィードバック系の極指定
poles=[0.4, 0.1];
//状態フィードバックゲインの計算
F=ppol(A,b,poles);
//状態フィードバックでのシステム行列
AF=(A - b*F);
Tz=syslin('d',AF,b,c);
Tzz=ss2tf(Tz);
//インパルス応答
u=[1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0];
y = flts(u,Tzz);
scf(1); plot(y,'-o');
//ステップ応答
u=[1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1]
y = flts(u,Tzz);
scf(2); plot(y,'-o');


“12. 状態フィードバック制御” に対して1件のコメントがあります。
コメントは受け付けていません。