5. 標準、校正、次元と次元式
標準
計測工学における「標準 (Standard)」とは、ある物理量を測定する際に、その測定結果を他の測定結果と比較するための基準となる物理量、あるいはその基準を定めるための規格や手順のことを指す。
例えば、長さの単位であるメートルは、国際的に定められた「メートル原器」と呼ばれる白金-イリジウム合金製の棒を基準としていた(1960年まで)。また、時間の単位である秒は、セシウム原子時計を基準としている。
標準が定められることによって、異なる測定器や異なる場所で測定された結果でも、同じ物理量を比較・統合することが可能となる。標準の規格化や管理は、国際度量衡局 (BIPM) が行っている。
標準
単位を物理的に実現したもの。
【例】 kg 原器(特殊な合金でできた質量1 kgの分銅)
メートル法の基本単位である1 kgの質量を現示する最高の標準器。
パリの国際度量衡局に保管されているものを国際キログラム原器といい、この質量が1 kgと約束されている。
最近では、物ではなく方法(物理現象)を標準として用いられることが多くなった。
【例】1メートル:1秒の299,792,458分の1の時間に光が真空中を伝わる距離。
1秒 :セシウム133原子の基底状態の二つの超微細構造準位の遷移に対応する放射の周期の91億9263万1770倍の継続時間。
(1967年に定義された)
測定器の校正とトレーサビリティ
計測工学における「校正 (Calibration)」とは、測定器や計測装置が、ある標準物質や標準器具によって、正確に測定できるように調整することをいう。
一般的に、測定器は製造時に精度が調整されているものの、使用中に劣化や誤差が生じる。また、異なる測定器を使用して測定した場合、微小な誤差が生じることがある。このような場合、測定器の校正を行うことで、正確に測定できるようにする。
校正を実施するタイミングは、基本的に測定機器を使用する前と使用後の2回が基本である。測定機器を常時使用して定期的に校正する場合は、周期をあらかじめ決めて、それに従って校正を行う。周期の決定はメーカーの推奨を基準とするか、測定機器の使用頻度から判断する。
校正は、測定器の精度や信頼性を保ち、正確な測定結果を得るために重要な手順である。
校正(較正)
測定器の指示が正しいことを保証するための検査作業。
標準器を用いて測定機器が表示する値と真の値の関係を求める。
計測工学における「トレーサビリティ (Traceability)」とは、ある測定値や測定結果が、ある基準(標準物質や標準器具など)に基づいて正確に測定されたことを示すことである。
トレーサビリティは、測定値や測定結果の信頼性や精度を保証するために重要で、測定器を校正するときに使用された基準が、他の標準と同等の正確さである場合、その測定器で得られた測定値や測定結果は、同等の正確さであることが期待される。また、トレーサビリティを確保することによって、国際的な比較や交換が可能になり、測定の正確性を保つことができる。
トレーサビリティは、測定値や測定結果を取得する際に必要な基準がどこから来たのかを追跡することで実現される。この追跡には、国際度量衡局(BIPM)による国際度量衡制度や、国内外の標準化団体によって定められた規格や手順が使用される。
トレーサビリティ
標準器の上位をたどり、国家標準にたどりつけること。
測定器の校正の種類
測定器の校正の種類は、以下の表のようにまとめられる。いずれにしても第三者による校正が望ましい。
※参考サイト:https://www.keyence.co.jp/ss/products/measure-sys/measurement-selection/environment/calibration-method.jsp

次元と次元式
「次元 (Dimension)」とは、物理量を表すために使用される性質の一つで、その物理量が表す対象の大きさや種類を表す。例えば、長さや時間、質量などが代表的な次元である。
「次元式 (Dimensional Formula)」とは、ある物理量の次元を表す式のことを指す。次元式は、物理量を表す単位の種類と、その単位が各基本次元に対して何乗されるかを表す指数から構成される。例えば、長さを表す次元式は「\([L]\)」、質量を表す次元式は「\([M]\)」、時間を表す次元式は「\([T]\)」とする。
次元式は、物理量がどのような性質を持つかを理解するために非常に重要である。また、次元式を用いることで、物理量の単位を変換することができる。例えば、長さをメートルからセンチメートルに変換する場合、「\(1 m = 100 cm\)」であることを次元式を用いて「\([L] = [L] \times 10^2\)」のように表現し、単位を変換することができる。
量の次元
ある一つの量をその体系の基本量を表す因数のべき乗の積として示す表現のこと。
【例】速度\(v\) は 長さ\(l\)と時間\(t\)の比で \(v=\frac{l}{t} =l \cdot t^{-1} \)である。
従って、速度\(v\)は、長さ\(L\)の\(1\)次元と時間\(T\)の \(-1\)次元の積なので次元式は、$$dim \; v = L^1 T^{-1}$$ となる。 ※dimは次元(dimension)の意味である。
次元式の一般式
\(L\):長さ、 \(M\):質量、 \(T\):時間、 \(I\):電流、 \(\theta\):温度、 \(N\):物質量、 \(J\):光度
とすると、次元の一般式は、$$dim \; A= L^{\alpha} \; M^{\beta} \; T^{\gamma} \;I^{\delta} \; \theta^{\epsilon} \; N^{\zeta} \; J^{\eta}$$である。
※指数(\( \alpha \; \beta \; \gamma \; \cdots\) )が全て0なら無次元となる。
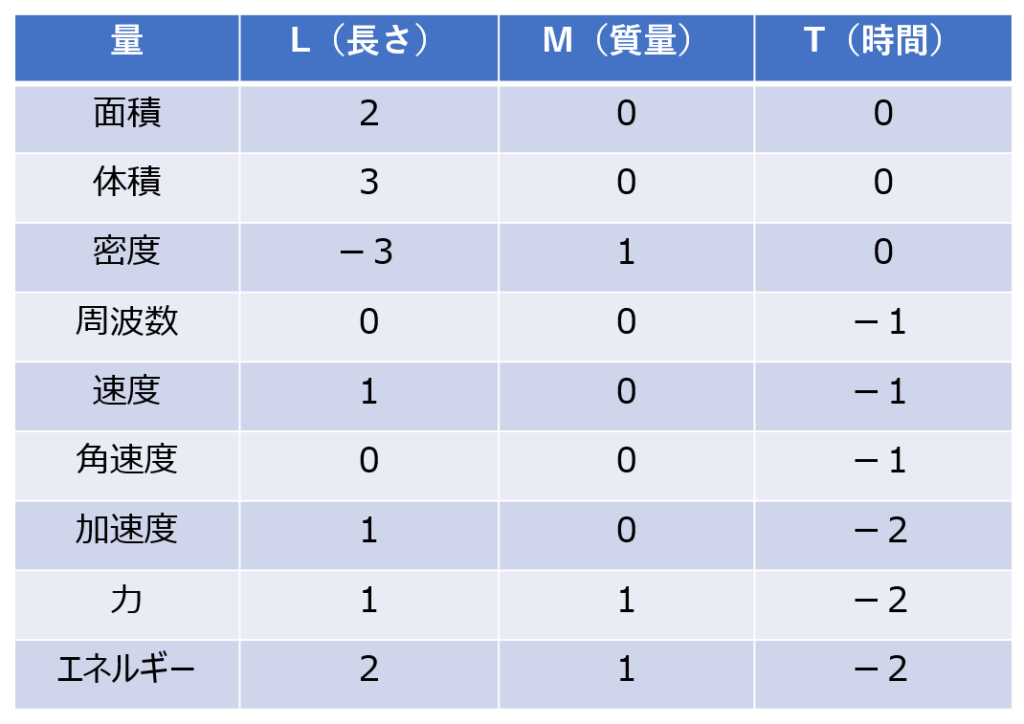
【例】周波数の単位 \(Hz =\frac{1}{s}\)
次元は \(T^{-1}\)となる。
L:長さ、 M:質量、
T:時間、 I:電流、
θ:温度、 N:物質量、
J:光度
(基本7単位で構成する)
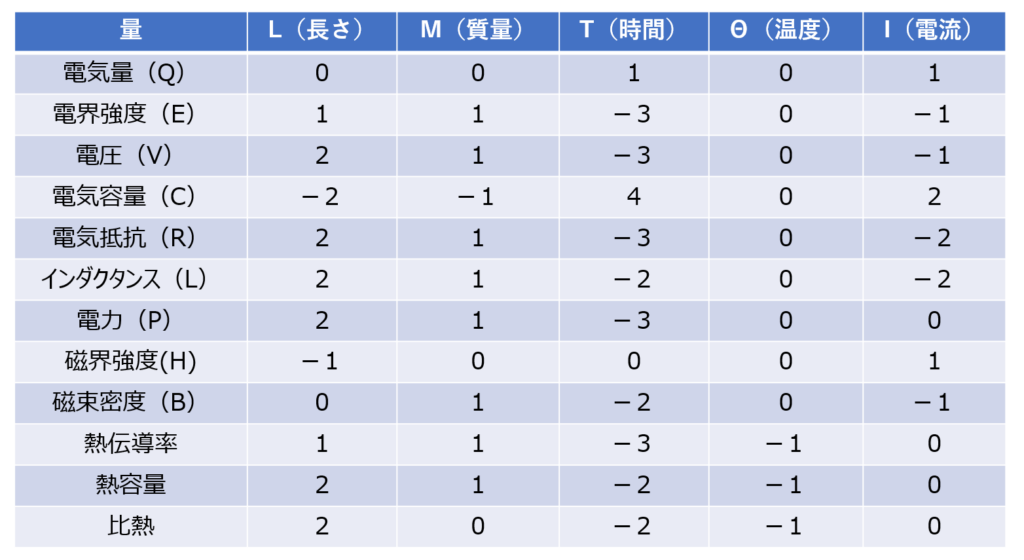
電気電子計測でよく表れる物理量の次元をまとめると以下となる。