6. 電源の内部抵抗
電源の内部抵抗は、電源内部に存在する抵抗要素や回路内の電気的な効果(リアクタンス等)によって生じる。内部抵抗は、電源出力が外部回路に接続されたとき、電源出力電圧の低下を引き起こし、回路の動作や測定値に影響を与える。
内部抵抗の例として、電池の内部抵抗は、電池の端子間で電流が流れる際の抵抗で、電池の材料や構造、製造方法などによって決まり、電池の種類によって異なる。内部抵抗が大きいと、電池から流れる電流が少なくなり、外部回路に供給される電力が少なくなる。これにより、外部回路の動作に影響を与える可能性がある。
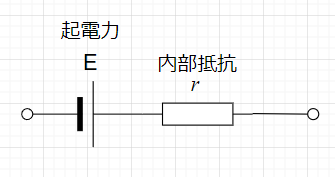
直流電圧源(例:電池)は、図「直流電圧源のモデル」のように、内部抵抗\(r\)と起電力\(E\)から成り立っている。
図のように外部回路が接続されていない状態では、電流が流れないので、\(r\)による電圧降下は、\(0\)[V]で、端子間の電圧は起電力そのものの\(E\)[V]である。電池であれば、電池単体での電圧である。
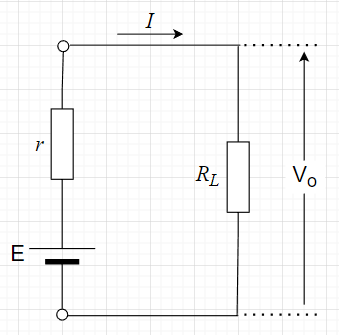
接続したときの出力電圧
内部抵抗\(r\)、起電力\(E\)の直流電圧源に負荷抵抗\(R_L\)を接続したときの出力電圧\(V_o\)を考える。
内部抵抗\(r\)と負荷抵抗\(R_L\)は直列接続になるので、電流\(I\)は、$$I = \frac{E}{r + R_L}$$となる。従って、出力電圧\(V_o\)は、$$V_o = R_L I = \frac{R_L}{r + R_L}E$$となる。また、$$V_o = E - rI = E - r \frac{E}{r + R_L} = \frac{R_L}{r + R_L}E$$とも表せる。
ここで、内部抵抗\(r\)が大きいときを考える。極端な例として、\(r \rightarrow \infty\)とすると、$$V_o = \lim_{r \rightarrow \infty} \frac{ \frac{R_L}{r}}{1+ \frac{R_L}{r}}E = 0 $$となる。
逆に、内部抵抗\(r \rightarrow 0\)とすると、$$V_o = \lim_{r \rightarrow 0} \frac{R_L}{r + R_L}E=E$$となる。
以上のことから、内部抵抗はできるだけ小さい方が良いことが分かる。
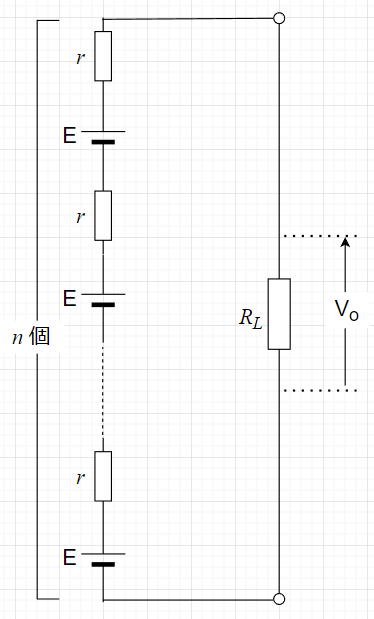
直流電圧源の直列接続
直流電圧源の直列接続は、例えば、電池の直列接続がある。この場合、出力電圧\(V_o\)はどのようになるか考える。
\(n\)個の電圧源を直列に接続して、負荷抵抗\(R_L\)を接続する。このときの出力電圧\(V_o\)を求める。
各電源の内部抵抗\(r\)は等しいと仮定すると、負荷\(R_L\)に流れる電流は、$$I = \frac{n\cdot E}{R_L + n \cdot r}$$となる。よって、負荷\(R_L\)への出力電圧\(V_o\)は、$$V_o = n \cdot E - n\cdot r\cdot I$$となる。
負荷抵抗\(R_L\)が小さいと、流れる電流\(I\)は大きくなり、電源の内部抵抗による電圧降下が大きくなる。また、内部抵抗による電力消費は\(I^2 nr\)と大きくなり、電源内部の発熱が大きくなる。
電源の直列接続では、内部抵抗が大きくなることに注意する必要がある。内部抵抗が大きい電源は、熱を発生しやすくなり、電源が長時間連続して負荷を駆動する場合、電源の効率が低下する。従って、内部抵抗が大きい電源は、負荷の安定性や電源の効率に影響を与える可能性がある。

