16. ディジタル再設計
制御器の設計におけるディジタル再設計とは、アナログ制御の方法をディジタル技術を利用した制御に変更することを指す。従来のアナログ制御では、制御信号は電圧や電流の変化で表現されていたが、ディジタル制御では信号をディジタルデータの形で扱う。このため、制御器内部の回路や処理方法が変わり、一般的に制御精度や信頼性が向上する。
ディジタル制御には、マイクロコントローラやフィールドプログラマブルゲートアレイ(FPGA)などのディジタル回路技術が活用される。これらのデバイスは、高速な処理能力や柔軟性があり、多様な制御システムに適用可能である。また、ディジタル制御では、センサから取得した信号を高精度で高速に処理できる場合、より正確な制御が可能になる。
ディジタル再設計
連続時間系の制御則を設計した後、サンプリング周期を決定し、ディジタル制御系のフィードバックゲインや補償器を決定する方法。
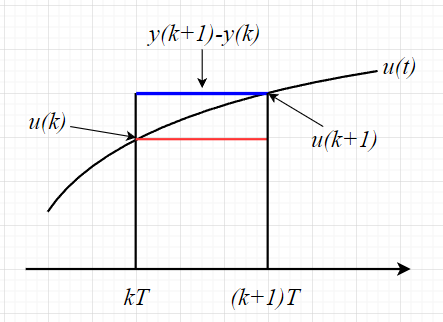
離散系の近似計算
図「離散系の近似計算」を参考に各近似法を考える。
幅が\(T\)で高さが赤線か青線の長方形の面積、もしくは、\(u(k)\)と\(u(k+1)\)を結んだ直線で囲んだ台形の面積を求めることを考える。
\(u(k+1)\)までの面積が\(y(k+1)\)、\(u(k)\)までの面積が\(y(k)\)である。従って、\(kT\)から\((k+1)T\)までの\(u(t)\)が囲む面積は、\(y(k+1) -y(k)\)である。
*前進差分(赤線の高さの長方形の部分の積分)
$$y(k+1) - y(k) = T u(k) $$なので、Z変換すると$$zY(z) - Y(z) = TU(z) \\ Y(z) =\frac{T}{z-1} U(z)$$よって、
積分演算:\(\frac{T}{z-1}\) 、 微分演算:\(\frac{z-1}{T}\)
*後進差分(青線の高さの長方形の部分の積分)
$$y(k+1) - y(k) = T u(k+1) $$なので、Z変換すると$$zY(z) - Y(z) = TzU(z) \\ Y(z) =\frac{Tz}{z-1} U(z)$$よって、
積分演算:\(\frac{Tz}{z-1}\) 、 微分演算:\(\frac{z-1}{zT}\)
*双一次Z変換(台形近似での積分)
$$y(k+1) - y(k) = \frac{T}{2}\left\{u(k+1) + u(k)\right\}$$なので、Z変換すると$$zY(z) -Y(z) = \frac{T}{2}\left\{zU(z) +U(z)\right\} \\ Y(z)= \frac{T}{2}\cdot \frac{z+1}{z-1} U(z)$$よって、
積分演算:\(\frac{T}{2}\cdot \frac{z+1}{z-1}\) 、 微分演算:\(\frac{2}{T}\cdot \frac{z-1}{z+1}\)となる。
従って、双一次Z変換を使うと、連続系の微分演算子\(\frac{d}{dt}\)がラプラス変換で\(s\)となり、さらに離散系へ変換するときは
$$ s \rightarrow \frac{2}{T}\cdot \frac{z-1}{z+1}$$とすれば良い。つまり、s領域で表した伝達関数を双一次Z変換で離散系へ変換できることになる。ただし、サンプリング時間\(T\)が大きくなると連続系への近似度が悪くなる。逆にサンプリング時間\(T\)が小さいと、前進差分、後進差分、双一次Z変換の差はなくなり、連続系への近似度が高くなる。
PID制御器のディジタル再設計【例】
*PI型の連続時間制御系をディジタル再設計する
制御対象は、$$P(s) = \frac{1}{s+ a}$$とする。また、制御器は、$$C(s)= \frac{1 +3 s}{4s}$$とする。$$s = \frac{2}{T}\cdot\frac{z-1}{z+1}$$ を使って、双一次Z変換で離散系へ変換する。$$C(z)=\frac{T(z+1)}{8(z-1)} + \frac{3}{4} = \frac{(6+T)z - (6-T)}{8(z-1)}$$となる。
また、制御対象は、Z.O.H. で\(P(s)\)を離散化すると$$P(z) = (1-z^{-1})\mathcal{Z}\left\{\frac{P(s)}{s}\right\} = \frac{1}{a} \left(\frac{1-e^{-aT}}{z - e^{-aT}} \right)$$となる。
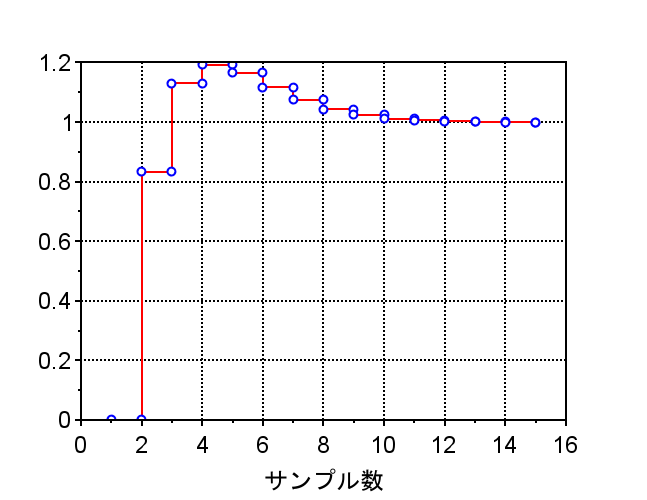
サンプリング時間 TT=1.0
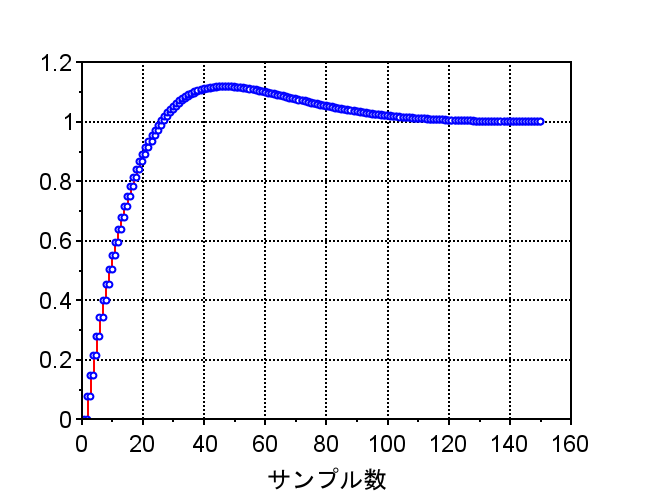
サンプリング時間 TT=0.1
Scilabでのシミュレーション
//PID制御器のディジタル再設計
clear;clf;
z=%z; s=%s;e=%e;
a=0.1;
P=1/(s+a); /*制御対象*/
C=(1+3*s)/(4*s); /*制御器*/
L=P*C;
T=L/(1+L);
Ts=syslin('c',T)
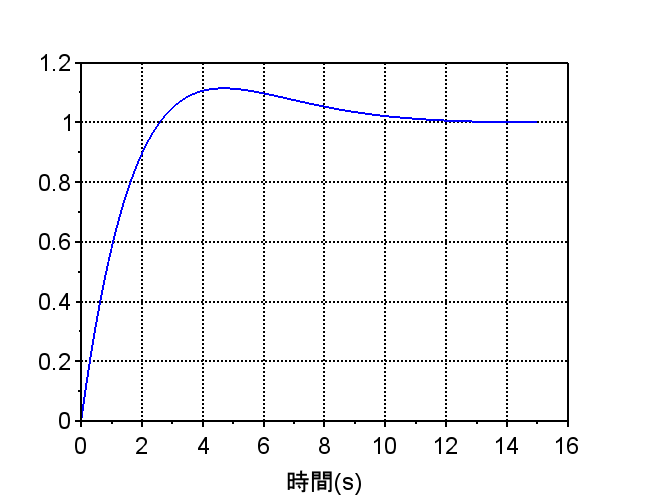
//連続時間系でのステップ応答
t=0:0.1:15;
y=csim('step',t,Ts);
scf(0); plot(t,y);
//ディジタル系への変換
TT=1.0; /*サンプリング時間(ここを変える)*/
Pz=(1/a)*((1-e^(-a*TT))/(z-e^(-a*TT)));
Cz=((6+TT)*z-(6-TT))/(8*(z-1));
Lz=Pz*Cz;
Tz=Lz/(1+Lz);
Tzz=syslin('d',Tz);
//離散時間系でのステップ応答
k=0:TT:(15/TT);
r(1:(15/TT))=1;
y = flts(r',Tzz);
scf(1); plot(y,'o-');
ステップ応答を比較すると、サンプリング時間により、応答が変わる。
サンプリング時間が長いと応答特性が劣化することが分かる。サンプリング時間が適正に設定できれば、連続系に近い応答が得られることが分かる。

