12. 直流ブリッジ回路
ブリッジ回路は、主に各種センサの抵抗値(インピーダンス)の変化を計測するために使用される。一般的には、ホイートストンブリッジ回路として知られており、直流ブリッジ回路では4つの抵抗素子を組み合わせて構成する。ブリッジ回路では、一つの抵抗素子の抵抗値が変化することで、ブリッジ回路のバランスが崩れ、その変化を計測することができる。この方法は、抵抗計や変位計と組み合わせて使用され、様々な計測や制御に応用されている。
また、計測用ブリッジ回路には、圧力センサや荷重センサ、温度センサなどのセンサにも使用される。これらのセンサは、機械的変形、圧力、温度の変化に応じて抵抗値が変化するので、ブリッジ回路を使って抵抗値の変化を検出し、その信号を増幅して測定する。
直流ブリッジ回路
ブリッジの平衡条件
図「直流ブリッジ回路」で考える。
ブリッジ回路では、$$R_1 \cdot R_4 = R_2 \cdot R_3$$が成立するとき、\(R_x\)に流れる電流が\(0\)となる。これをブリッジの平衡条件という。
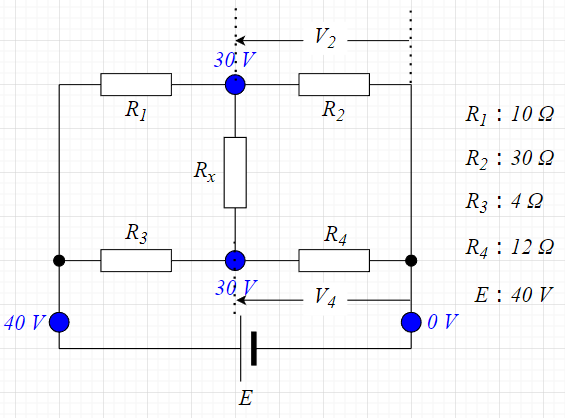
具体的に図「直流ブリッジ回路」の設計値で考える。
電源\(E\)の負極側を基準の\(0 \; V\)とすると、正極側は\(40\;V\)なので、\(R_1\)の左側が\(40\;V\)、\(R_2\)の右側が\(0 \; V\)である。
分圧の式から、$$V_2 = \frac{R_2}{R_1 + R_2}E=\frac{30}{10+30}40=30\;V$$となる。同様に、$$V_4 = \frac{R_4}{R_3 + R_4}E=\frac{12}{4+12}40=30\;V$$となる。従って、\(R_x\)の両端が同電位(同じ電圧)であるので、\(R_x\)には電流は流れないことになる。
\(V_2 = V_4\)が成立するとき、ブリッジ回路は平衡なので、式を整理すると、$$ \frac{R_2}{R_1 + R_2}E = \frac{R_4}{R_3 + R_4}E \\ \frac{R_2}{R_1 + R_2} = \frac{R_4}{R_3 + R_4} \\(R_3 + R_4)R_2 = (R_1 + R_2)R_4 $$なので、以上より、$$ R_2 \cdot R_3 = R_1\cdot R_4$$ とブリッジの平衡条件が求まる。


“12. 直流ブリッジ回路” に対して1件のコメントがあります。
コメントは受け付けていません。