15. 重ねの理(重ね合わせの理)
重ねの理とは、「2個以上の複数の電源がある回路で、回路の任意の点の電流及び電圧はそれぞれの電源が単独で存在した場合の値の和に等しい」という理論である。これは、線形回路で成り立つ理論で、非線形回路では成り立たない。
重ねの理により、一つの電源だけを残して他の電源を取り除いた分離回路の電流や電圧を解析することを複数ある電源の数の分だけ取り出すことを繰り返し、得られた電流や電圧を合成していけば、元の回路の電流や電源を求めることができる。ここで、取り除く電源が、電圧源であればその部分は短絡し、電流源であればその部分は開放するものとする。
線形性
線形とは、グラフにしたとき直線となるような数学的関係のことをいう。具体的には、ある関数\(y=f(x)\)(回路では入出力関係:入力\(x\)、出力\(y\))において、\(f(x+y)=f(x) + f(y) \\ f(ax ) =af(x) \)が成立することをいう。
例えば、一次関数\(f(x)=kx\)であれば、\(f(x+y) = k(x+y)=kx+ky\\ =f(x) + f(y) \\ f(ax) = kax=af(x)\)となり線形であることが分かる。
二次関数\(g(x)=kx^2\)の場合は、\(g(x+y)=k(x+y)^2 \\= kx^2 + ky^2+2kxy \ne g(x)+g(y)\)となるので、線形ではない(非線形)。
重ねの理を使った回路解析【例】
キルヒホッフの法則を使った場合
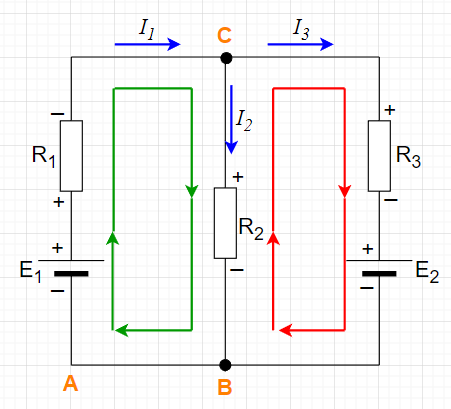
C点において、KCLにより、$$I_1 = I_2 + I_3$$KVLより、緑線の閉ループは、$$E_1-R_1I_1-R_2I_2 =0$$ また、赤線の閉ループは、$$R_2I_2-R_3I_3-E_2=0$$となる。従って、$$I_1 - I_2 - I_3 = 0 \\R_1 I_1 + R_2 I_2 = E_1 \\R_2 I_2 - R_3 I_3 = E_2$$の3元連立方程式となる。これを解くと、$$I_1 = \frac{E_1R_3 + (E_1 - E_2)R_2}{R_2(R_3 + R_1) + R_1 R_3} =\frac{E_1R_3 + (E_1 - E_2)R_2}{R_1 R_2 + R_2 R_3 + R_3 R_1} $$ $$I_2 = \frac{E_1 R_3 + E_2 R_1}{R_2(R_3 + R_1) + R_1 R_3}= \frac{E_1 R_3 + E_2 R_1}{R_1 R_2 + R_2 R_3 + R_3 R_1}$$ $$I_3 = \frac{(E_1 - E_2)R_2 - E_2 R_1}{R_2(R_3 + R_1) + R_1 R_3}=\frac{(E_1 - E_2)R_2 - E_2 R_1}{R_1 R_2 + R_2 R_3 + R_3 R_1}$$となる。
重ねの理を使った場合
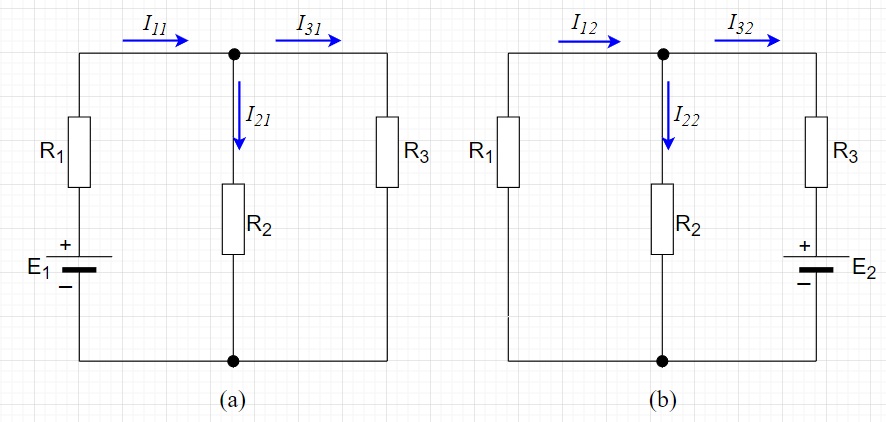
図「キルヒホッフの法則での解析」と同じ方向で電流を仮定する。求める\(I_1, I_2, I_3\)は、$$I_1 = I_{11} + I_{12} \\ I_2 = I_{21} + I_{22} \\ I_3 = I_{31} + I_{32}$$である。
図「重ねの理を使った解析」の(a)は、電源\(E_2\)を取り除いてその部分を短絡したものである。この時、\(R_2 , R_3\)は並列接続となり、電流\(I_{11}\)は、$$I_{11} = \frac{E_1}{R_1 + \frac{R_2 R_3}{R_2 + R_3}} = \frac{E_1(R_2 + R_3)}{R_1(R_2 + R_3) + R_2 R_3}=\frac{E_1(R_2 + R_3)}{R_1R_2 + R_2 R_3 + R_3 R_1}$$となる。\(I_{21} , I_{31}\)は分流の式を使って、$$I_{21} = \frac{R_3}{R_2 + R_3}I_{11} = \frac{E_1 R_3}{R_1R_2 + R_2 R_3 +R_3 R_1} $$ $$ I_{31} = \frac{R_2}{R_2 + R_3}I_{11} = \frac{E_1 R_2}{R_1 R_2 + R_2 R_3 + R_3 R_1}$$となる。
同様に、図「重ねの理を使った解析」の(b)は、電源\(E_1\)を取り除いてその部分を短絡したものである。この時、\(R_1 , R_2\)は並列接続となり、電流\(I_{32}\)は、$$I_{32} = -\frac{E_2}{R_3 + \frac{R_1 R_2}{R_1 + R_2}} = -\frac{E_2(R_1 + R_2)}{R_1 R_2 + R_2 R_3 + R_3 R_1}$$となる。\(I_{12} , I_{22}\)は分流の式を使って、$$I_{12} = \frac{R_2}{R_2 + R_1}I_{32}= -\frac{E_2 R_2}{R_1 R_2 + R_2 R_3 + R_3 R_1}$$ $$I_{22} = \frac{R_1}{R_1 + R_2}I_{32} = \frac{E_2 R_1}{R_1 R_2 + R_2 R_3 + R_3 R_1}$$となる。ただし、\(I_{12}, I_{32}\)は電流の向きが逆になるので、負の値となる。
以上を重ね合わせると$$I_1 = I_{11} + I_{12} = \frac{E_1(R_2 + R_3)}{R_1 R_2 + R_2 R_3 + R_3 R_1} -\frac{E_2 R_2}{R_1 R_2 + R_2 R_3 + R_3 R_1} = \frac{E_1R_3 + (E_1 - E_2)R_2}{R_1 R_2 + R_2 R_3 + R_3 R_1}$$ $$I_2 = I_{21} + I_{22} = \frac{E_1 R_3}{R_1 R_2 + R_2 R_3 + R_3 R_1} + \frac{E_2 R_1}{R_1 R_2 + R_2 R_3 + R_3 R_1} = \frac{E_1 R_3 + E_2 R_1}{R_1 R_2 + R_2 R_3 + R_3 R_1}$$ $$I_3 = I_{31} + I_{32} = \frac{E_1 R_2}{R_1 R_2 + R_2 R_3 + R_3 R_1} -\frac{E_2(R_1 + R_2)}{R_1 R_2 + R_2 R_3 + R_3 R_1}= \frac{(E_1 - E_2)R_2 - E_2 R_1}{R_1 R_2 + R_2 R_3 + R_3 R_1} $$となる。この結果は、当然のことながらキルヒホッフの法則で求めたものと一致する。

