17. 抵抗とコンダクタンス
抵抗とコンダクタンスは、電気回路の基本的な物理量であり、電流の流れを制御する要素(部品)である。
抵抗は、電気回路において電流を流すとき、その流れを制限する物理的な現象を表す。つまり、電圧を印加しても、抵抗により電流が自由に流れることができず、一定の制限を受ける。抵抗の単位はオーム(\(\Omega\))で表す。
コンダクタンスは、電気回路における電気伝導(導電)の度合いを表す。つまり、電流が自由に流れることができる度合いを表し、電気回路の性質を決定する。コンダクタンスは、抵抗の逆数で表され、単位はジーメンス(\(S\))で表す。導体や半導体など、電気を良く通す性質を持つ物質は、大きいコンダクタンスを持つ。
抵抗
抵抗は、$$R = \frac{V}{I} \; [\Omega]$$と表せる。
\(V \; [V]\):電圧、\(I \; [A]\):電流である。
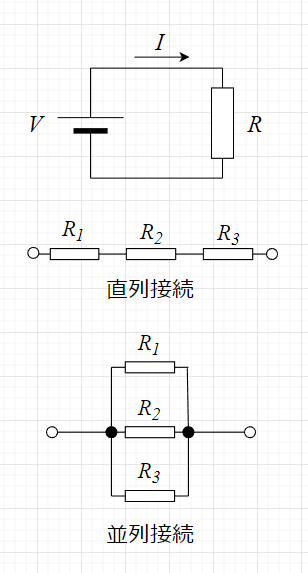
図「抵抗」で考える。
直列接続の合成抵抗 \(R_s\)は、$$R_s = R_1 + R_2 + R_3 \;[\Omega]$$である。抵抗\(n\)個の直列接続では、$$R_s = R_1 + R_2 + R_3 + \cdots + R_n \; [\Omega]$$となる。
並列接続の合成抵抗 \(R_p\)は、$$\frac{1}{R_p} =\frac{1}{ R_1} +\frac{1}{R_2} + \frac{1}{R_3} \; [S]$$である。抵抗\(n\)個の並列接続では、$$\frac{1}{R_p} =\frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + \cdots + \frac{1}{R_n} \; [S]$$となる。
※抵抗の直列接続、並列接続については、こちらへ。
コンダクタンス
コンダクタンス\(G\)は、抵抗\(R\)の逆数で表され、単位はジーメンス\([S]\)である。$$G = \frac{1}{R} = \frac{I}{V} \; [S]$$と表せる。\(V \; [V]\):電圧、\(I \; [A]\):電流、\(R\; [\Omega]\):抵抗である。
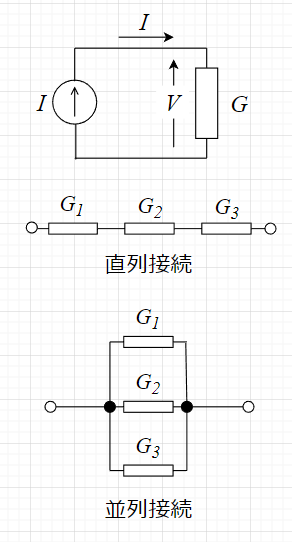
図「コンダクタンス」の電流源の図で考えると、$$I=VG$$となる。
コンダクタンスの直列接続では、\(G_1 = \frac{1}{R_1}\)なので、$$\frac{1}{G_s}= \frac{1}{G_1} + \frac{1}{G_2} +\frac{1}{G_3} \; [\Omega]$$となる。
コンダクタンスの並列接続では、抵抗の並列接続の式から、$$G_p = G_1 + G_2 + G_3 \; [S]$$となる。
従って、コンダクタンスは、抵抗の並列接続のときに使うと便利である。
コンダクタンスのオームの法則
コンダクタンスでオームの法則を表すと、$$G =\frac{I}{V} \;[S]\;\;\;\;\;\; I = GV \; [A] \;\;\;\;\; V= \frac{I}{G} \; [V]$$となる。

