21. 正弦波交流のベクトル表示

正弦波交流は、一定の振幅を持ち、周波数が一定の交流電圧または電流を表す。これをベクトル表示する方法は、複素数の指数関数形式を用いて行うことができる。正弦波交流のベクトル表示では、振幅を大きさ、位相角を方向として、複素平面上で表す。

具体的には、正弦波の式を以下のように書き換える。$$v(t) = V_m \sin(\omega t + \theta)$$ここで、\(V_m\)は振幅、\(\omega\)は角周波数、\(\theta\)は初期位相角を表す。この式をオイラーの公式を用いて書き換えると、$$e^{j(\omega t + \theta)}= \cos(\omega t + \theta) + j \sin(\omega t + \theta)$$なので、$$v(t) = V_m \mathrm{Im}\left\{e^{j(\omega t + \theta)}\right\}$$と表せる。

ここで、\(j\)は虚数単位である。この式は、\(e^{j(\omega t + \theta)}\)という複素数の虚部をとることで正弦波の式と等価になることを示している。
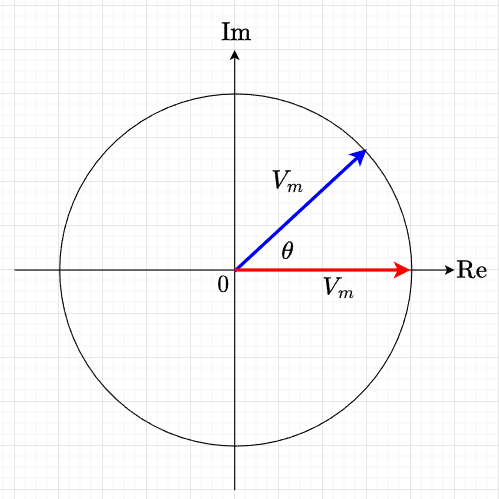
この式を複素平面上に表すと、図「正弦波交流のベクトル表示」のようになる。複素平面上の実数軸（\(\mathrm{Re}\)）が実部、虚数軸（\(\mathrm{Im}\)）が虚部を表している。この図の赤矢印で示すベクトルは、初期位相角が0の場合を表している。初期位相角が\(\theta\)の場合は、複素平面上でのベクトルが\(\theta\)だけ回転して青矢印で示すベクトルとなる。大きさはいずれも\(V_m\)（振幅）である。
このように、正弦波交流をベクトル表示することで、振幅と位相角を一度に表すことができる。
図「正弦波交流のベクトル表示」の例では、赤矢印のベクトルは初期位相角が０なので、$$v_1(t) = V_m \sin \omega t$$であり、青矢印のベクトルは初期位相角が\(\theta\)なので、$$v_2(t) = V_m \sin(\omega t + \theta)$$である。このとき、\(v_1(t),v_2(t)\)は同一の角周波数\(\omega\)で同じ反時計方向に回転すると、それぞれのベクトル間の相対的な位置は、時間\(t\)に関係なく一定であるから、ベクトル間の相互間の関係は静止したベクトルと考えることができる。従って、ベクトルが回転していることを省略して、正弦波交流をベクトルで取り扱う時は、静止ベクトルとする。どちらかを基準ベクトルとして実数軸（\(\mathrm{Re}\)）上にとるとよい。この例の場合は、\(v_1(t)\)のベクトル（赤矢印）を基準としている。
なお、\(v_1(t),v_2(t)\)の正弦波は、これらのベクトルが角周波数\(\omega\)で反時計方向に回転するときの先端の虚数軸（\(\mathrm{Im}\)）上への正射影となっている。