22. 交流回路における抵抗の作用

回路における抵抗は、電気エネルギーを熱エネルギーに変換する役割を持つ。つまり、抵抗に電流が流れると、電気エネルギーは抵抗の中で消費され、その結果として抵抗が熱を発生させる。このように、抵抗によって電力が消費されるため、抵抗は回路においてエネルギー損失を引き起こす。また、抵抗は交流回路においても同様に働く。交流電圧が抵抗に印加されると、抵抗に交流電流が流れる。このとき、抵抗に流れる電流とその電圧降下（抵抗の両端の電圧）は同じ位相となる。

図「抵抗\(R\)だけの回路」において、抵抗\(R \; [\Omega]\)に交流起電力\(e = E_m \sin \omega t \; [V]\)を加えると、抵抗\(R\)の両端に生じる電圧\(e \; [V]\)は、\(v=e\)の関係から、$$v = V_m \sin \omega t \; [V] \cdots \cdots (1)$$となる。ここで、\(V_m = E_m \; [V]\)：振幅である。

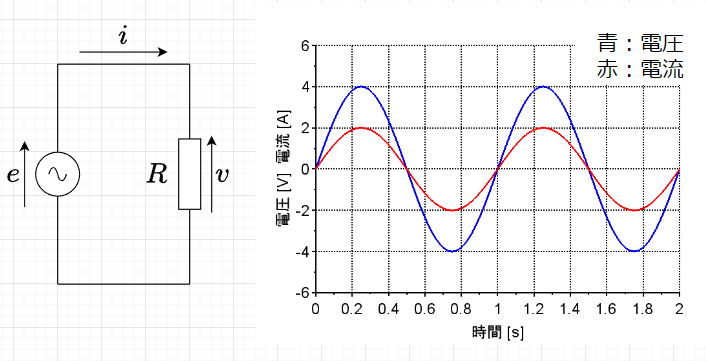
また、抵抗\(R\)に流れる電流\(i \; [A]\)は、オームの法則から、$$i = \frac{v}{R} = \frac{V_m \sin \omega t}{R} = I_m \sin \omega t \; [A] \cdots \cdots (2)$$となる。ここで、\(I_m = \frac{V_m}{R}\)である。
以上から、図「抵抗\(R\)だけの回路」の右図に示すように、\(v\)と\(i\)は同相（位相差が無い）で、最大値（振幅）が\(V_m,I_m\)、実効値が\(V=\frac{V_m}{\sqrt{2}}, \;I=\frac{I_m}{\sqrt{2}}\)の正弦波となる。また、電圧、電流の実効値\(V\;[V] , I\;[A]\)の間には、$$V = RI \; [V]$$の関係がある。

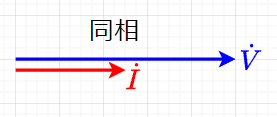
図「抵抗\(R\)だけの回路のベクトル図」は、電圧\(\dot{V}\)、電流\(\dot{I}\)のベクトル図である。
\(V,I\)をベクトル図で示すときは、角周波数がともに\(\omega \; [\mathrm{rad}/s]\)で一定であるから、これらの相対関係は時間\(t\)に無関係となるので、\(t=0\)の状態で表示する。従って、\( \dot{V}, \;\dot{I} \)の位相は、\(t=0\)における初期位相で示すことになる。
図「抵抗\(R\)だけの回路のベクトル図」では、\(\dot{V}, \; \dot{I} \)の位相は、式\((1),(2)\)からともに零なので同相である。