24. 交流回路におけるキャパシタの作用

キャパシタ（コンデンサ）は電荷を貯めることができる素子、つまり電気的な容量を持つ素子である。キャパシタは、交流信号を通過させることができるが、直流信号を通過させることができない。この特性を利用して、キャパシタは交流信号のフィルタリングや直流のブロックなど、様々な用途に使用される。
キャパシタに電荷を蓄積すると、それに対応してキャパシタ両端子間の電圧が上昇する。逆に、キャパシタから電荷が放出されると、電圧は下がる。このようなキャパシタの特性を利用することでキャパシタは以下のような作用をする。
１．フィルタリング：交流信号において、キャパシタは高周波成分を通過させ、低周波成分をブロックすることができる。この特性を利用して、キャパシタはフィルタ回路に使用される。
２．電圧安定化：キャパシタは電圧を蓄積することができるため、交流信号の波形が変化する際に、電圧を安定化することができる。このため、キャパシタは電源回路やスムーサ回路などで使用される。
その他、キャパシタは交流回路のカップリングコンデンサやディジタル回路のバイパスコンデンサなど、様々な重要な役割を果たす。

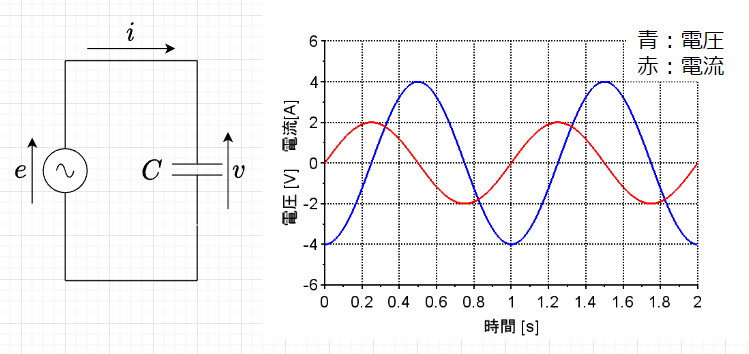
図「キャパシタ\(C\)だけの回路」において、静電容量\(C \; [F]\)のキャパシタに交流起電力$$e = E_m \sin \omega t \;[V]$$を加える。このときキャパシタ\(C\)の両端に生じる電圧\(v\)は、\(v=e\)の関係から、$$v = V_m \sin \omega t \;[V] \;\cdots\cdots (1)$$となる。ここで、\(E_m = V_m\)（振幅）である。

従って、キャパシタ\(C\)には、電荷\(q\)が蓄えられる。\(q = Cv = C V_m \sin \omega t \;[C]\)
電流\(i\)は、時間に対する移動する電荷の割合であるから、$$i = \frac{dq}{dt} = C \frac{dv}{dt} = C\frac{d}{dt}\left(V_m \sin \omega t \right) = \omega C V_m \cos \omega t \\= I_m \sin \left( \omega t + \frac{\pi}{2} \right) \; [A] \;\cdots\cdots (2)$$となる。なお、\(I_m = \omega C V_m\)である。
式\((1),(2)\)から、電流\(i\)が電圧\(v\)より\(\frac{\pi}{2} \;[\mathrm{rad}]\)だけ位相が進むことが分かる。図「キャパシタ\(C\)だけの回路」の右図の波形のようになる。

電圧の実行値、電流の実効値をそれぞれ\(V \; [V],\;\;I\;[A]\)とすると、電圧と電流の関係は、$$V=\frac{I}{\omega C} = \frac{1}{\omega C} I \;[V]$$となる。ここで、\(\frac{1}{\omega C} \; [\Omega]\)は容量性リアクタンスと呼ばれ、抵抗のように電流を制限する働きがある。単位は\(\Omega\)である。

この容量性リアクタンスは、記号\(X_C\)で表され、$$X_C = \frac{1}{\omega C} = \frac{1}{2 \pi f C} \; [\Omega]$$である。容量性リアクタンスの大きさは角周波数（周波数）\(\omega =2\pi f\)に依存するので、周波数が高いほど、つまり、電流の変化が大きいほど電流の流れを妨げる\(X_C\)は小さくなる。すなわち、高周波数に対しては電流が流れやすくなる。逆に電流の変化が無いとき、すなわち、直流（\(\omega = 0\)）では\(X_C\)は\(\infty\)となる。すなわち、直流成分はカットすることになる。
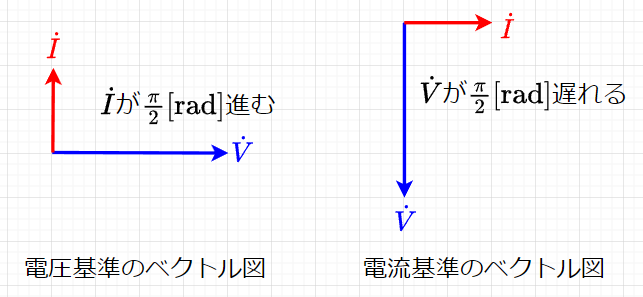
電圧と電流の関係をベクトル図で表すと、図「キャパシタ\(C\)だけの回路のベクトル図」のように電圧\(\dot{V}\)、電流\(\dot{I}\)のベクトル図として表せる。
\(V,I\)をベクトル図で示すときは、角周波数がともに\(\omega \; [\mathrm{rad}/s]\)で一定であるから、これらの相対関係は時間\(t\)に無関係となるので、\(t=0\)の状態で表示する。従って、\( \dot{V}, \;\dot{I} \)の位相は、\(t=0\)における初期位相で示すことになる。
図「キャパシタ\(C\)だけの回路のベクトル図」では、式\((1),(2)\)で\(\dot{I}, \; \dot{V} \)の初期位相がそれぞれ\(\pi/2[\mathrm{rad}], \;\; 0 [\mathrm{rad}]\)であるから、図「キャパシタ\(C\)だけの回路のベクトル図」の「電圧基準のベクトル図」のようになる。また、電流\(\dot{I}\)を基準に描くと「電流基準のベクトル図」のようになる。
一般にベクトル図を描く場合、直列回路では各素子に共通要素の電流\(I\)を、並列回路では各素子に共通な要素の電圧\(V\)を基準にして描くことが多い。