26. RLC直列回路

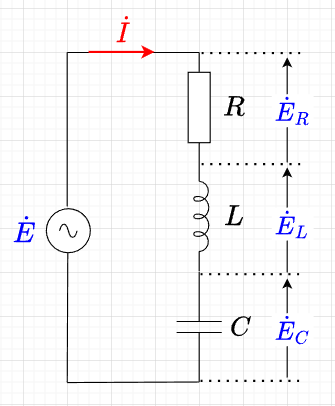
図「\(RLC\)直列回路」のように抵抗\(R \; [\Omega]\)、インダクタンス\(L \;[H]\)、キャパシタンス\(C \;[F]\)を直列に接続した回路に\(\dot{E} \; [V]\)の電圧を加えた場合を考える。回路に\(i = I_m \sin \omega t\)の電流が流れているとすると、\(R\)による電圧降下は、$$e_R = R I_m \sin \omega t$$\(L\)による電圧降下は、$$e_L = \omega L I_m \sin \left(\omega t + \frac{\pi}{2} \right)$$\(C\)による電圧降下は、$$e_C= \frac{1}{\omega C} I_m \sin \left(\omega t - \frac{\pi}{2} \right)$$となる。ここで、\(I_m \)は電流の振幅、電流の実効値は、\(\frac{I_m}{\sqrt{2}}\)である。従って、\(I_m = \sqrt{2} I\)である。

以上より、この直列回路の両端子間に加わっている全電圧は、これらの電圧降下の和であるから、$$e = e_R + e_L + e_C \\=R I_m \sin \omega t + \omega L I_m \sin\left( \omega t + \frac{\pi}{2}\right) + \frac{I_m}{\omega C} \sin\left( \omega t - \frac{\pi}{2}\right) \\ = R I_m \sin \omega t + \left(\omega L - \frac{1}{\omega C} \right) I_m \sin \left( \omega t + \frac{\pi}{2} \right) \\=\sqrt{R^2 + \left(\omega L - \frac{1}{\omega C} \right)^2} \cdot I_m \left\{\frac{R}{\sqrt{R^2 + \left(\omega L - \frac{1}{\omega C} \right)^2} } \sin \omega t + \frac{\omega L - \frac{1}{\omega C}}{\sqrt{R^2 + \left(\omega L - \frac{1}{\omega C} \right)^2} } \cos \omega t \right\} \\ =\sqrt{R^2 + \left(\omega L - \frac{1}{\omega C} \right)^2} \cdot I_m \sin (\omega t + \theta) \; [V]$$ ただし、$$\theta = \tan^{-1} \frac{\omega L - \frac{1}{\omega C}}{R}$$となる。

\(R , L, C\)のそれぞれの電圧を\(\dot{E}_R , \dot{E}_L , \dot{E}_C\)とし、電流を\(\dot{I}\)とすれば、$$E_R = RI \;\;\;\;\; E_L = X_L I = \omega L I \;\;\;\;\; E_C=X_C I = \frac{I}{\omega C}$$ここで、\(E, \; I\)は実効値である。\(\dot{E}_R\)は電流と同相、\(\dot{E}_L\)は\(\dot{I}\)より\(\pi /2\)　位相進み、\(\dot{E}_C\)は\(\dot{I}\)より\(\pi /2\)　位相遅れなので、ベクトル図は、図「\(RLC\)直列回路のベクトル図」となる。

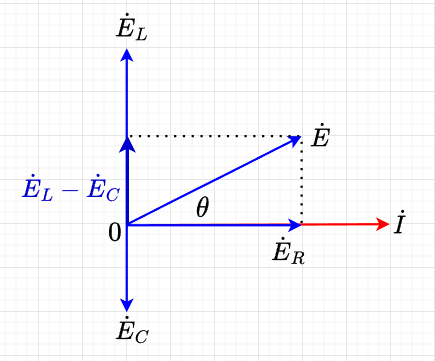
従って、全電圧\(E\)は、$$E = \sqrt{{E_R}^2 + (E_L - E_C)^2} = \sqrt{(RI)^2 + \left(\omega L I - \frac{1}{\omega C} I \right)^2} \\ = \sqrt{R^2 + \left(\omega L -\frac{1}{\omega C} \right)^2 }I = \sqrt{R^2 + (X_L -X_C)^2} I = \sqrt{R^2 + X^2} I = Z I \;[V]$$よって、$$I = \frac{E}{\sqrt{R^2 + \left(\omega L -\frac{1}{\omega C} \right)^2 }} = \frac{E}{Z} \; [A]$$ $$Z = \sqrt{R^2 + \left(\omega L -\frac{1}{\omega C} \right)^2 } \; [\Omega]$$となる。また、\(\dot{E} ,\; \dot{I}\)の位相角\(\theta\)は、$$\theta = \tan^{-1} \frac{\omega L - \frac{1}{\omega C}}{R}$$である。この場合、\(\omega L - \frac{1}{\omega C} = X\)が正ならば、\(\theta\)も正で電圧は電流より位相進みで、回路は誘導性となり、\(X\)が負であれば、\(\theta\)も負で電圧は電流より位相遅れで、回路は容量性となる。

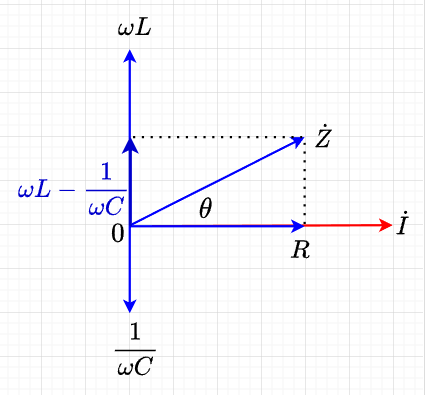
図「\(RLC\)直列回路のベクトル図」において、$$E_R = RI \;\;\;\;\; E_L = \omega L I \;\;\;\; E_C= \frac{I}{\omega C} \;\;\;\; E =Z I $$であるから、各式の右辺にかかっている\(I\)で割っても大きさの対比は変わらない。従って、図「インピーダンスのベクトル図」のように電圧の相互関係と同様にインピーダンスの関係をベクトル図で表すことができる。また、図から明らかなようにインピーダンスの偏角\(\theta\)は、$$\theta = \tan^{-1} \frac{\omega L - \frac{1}{\omega C}}{R}$$となる。