32. 交流回路の解析
交流におけるオームの法則
直流回路におけると同様に、導体に流れる交流電流\(\dot{I}\)は電位差\(\dot{V}\)に比例する。比例定数を\(1/\dot{Z}\)とすると、$$\dot{I} = \frac{\dot{V}}{\dot{Z}} \; [A] ,\;\;\;\;\;\; \dot{V} = \dot{Z} \dot{I} \; [V]$$が成り立つ。\(\dot{Z}\)は複素インピーダンスで、$$\dot{Z} = R + j X \; [\Omega]$$である。ここで、\(R\):抵抗、\(X\):リアクタンスである。
また、アドミタンスは、$$\dot{Y} = \frac{1}{\dot{Z}} = \frac{1}{R +jX} = \frac{R}{R^2 + X^2} - j \frac{X}{R^2 + X^2} =G - jB \;[S]$$と表せる。
なお、このようにオームの法則に従う回路を線形回路といい、従わない回路を非線形回路という。この「基礎電気回路」では、線形回路を扱っている。
キルヒホッフの法則
オームの法則から導かれたキルヒホッフの法則も、交流回路において、複素インピーダンスを用いると直流回路と同様に表せる。
KCL(キルヒホッフの電流則)
KCL:回路網内の任意の接続点に流入する電流と、その点から流出する電流の総和が等しい。つまり、流入電流を正(+)、流出電流を負(ー)として、$$\sum \dot{I} = 0$$
図「KCLの例」では、流入電流の符号を正(+)、流出電流の符号を(負)とすると、$$\dot{I}_1 + \dot{I}_3 - \dot{I}_2 - \dot{I}_4 = 0$$となる。
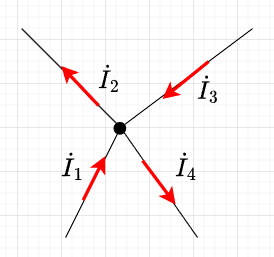
KVL(キルヒホッフの電圧則)
KVL:回路網内の任意の閉回路について、閉ループに沿って周回するとき、そのループに沿って電位をたどった時、電圧の総和(起電力と電圧降下の総和)が零になる。つまり、$$\sum \dot{E} - \sum \dot{Z} \dot{I}= 0$$もしくは、$$\sum \dot{E} =\sum \dot{Z} \dot{I}$$と表せる。
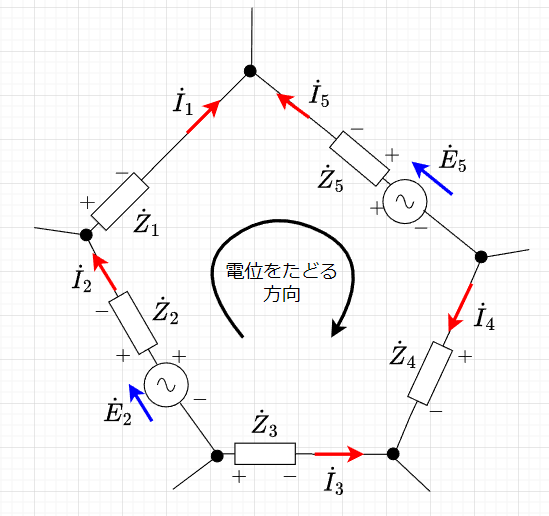
図「KVLの例」で電位をたどる方向で電圧の総和を求めると、$$-\dot{Z}_1 \dot{I}_1 + \dot{Z}_5 \dot{I}_5 - \dot{E}_5 - \dot{Z}_4 \dot{I}_4 + \dot{Z}_3 \dot{I}_3 + \dot{E}_2 - \dot{Z}_2 \dot{I}_2 = 0$$となる。ここで、図中の電流の方向は任意に設定し、各素子で、電位の高い方に\(+\)、電位の低い方に\( -\)を付けている。電位をたどる方向で、\(+ \rightarrow -\)のときは\(-\)、つまり減算として、\(- \rightarrow +\)のときは\(+\)、つまり加算とする。
先の式を整理すると、$$\dot{Z}_1 \dot{I}_1 + \dot{Z}_2 \dot{I}_2 - \dot{Z}_3 \dot{I}_3 + \dot{Z}_4 \dot{I}_4 - \dot{Z}_5 \dot{I}_5 - \dot{E}_2 + \dot{E}_5 = 0$$となる。また、閉ループにおいて、「起電力の総和=電圧降下の総和」と考えると、$$\dot{E}_2 - \dot{E}_5 = \dot{Z}_1 \dot{I}_1 + \dot{Z}_2 \dot{I}_2 - \dot{Z}_3 \dot{I}_3 + \dot{Z}_4 \dot{I}_4 -\dot{Z}_5 \dot{I}_5 $$と表せる。
インピーダンス直並列回路
インピーダンス直列回路の一般式
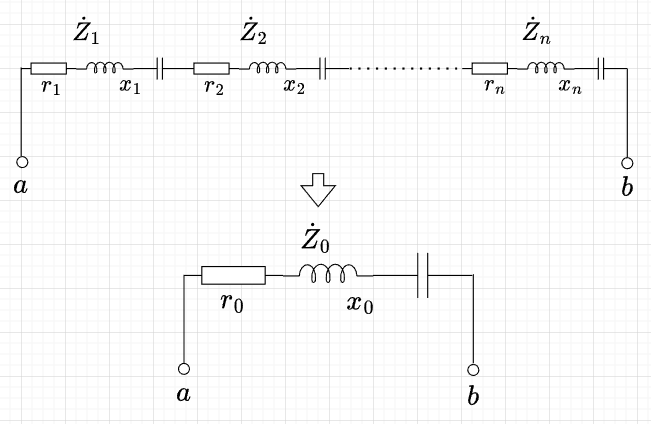
図「インピーダンス直列回路」のように\(n\)個のインピーダンス\(\dot{Z}_1 = r_1 +j x_1 , \; \dot{Z}_2 = r_2 +j x_2 , \; \cdots, \; \dot{Z}_n = r_n +j x_n \)が直列に接続された回路の端子\(a-b\)間に電圧\(\dot{E}\)を加えた時、回路に流れる電流\(\dot{I}\)と各インピーダンスの電圧降下\(\dot{E}_1,\; \dot{E}_2, \;\cdots,\; \dot{E}_n\)の関係は、$$\dot{E}_1 = \dot{Z}_1 \dot{I} ,\;\;\;\dot{E}_2 = \dot{Z}_2 \dot{I} ,\;\;\;\cdots, \; \dot{E}_n= \dot{Z}_n \dot{I} $$となる。これらの和が端子間の電圧\(\dot{E}\)となるから、$$\dot{E} = \dot{E}_1 + \dot{E}_2+ \cdots +\dot{E}_n = \sum_{i=1}^n \dot{Z}_i \dot{I} = I \sum_{i=1}^n \dot{Z}_i \;[V]$$である。従って、$$\dot{Z}_0 = \frac{\dot{E}}{\dot{I}} = \sum_{i=1}^n \dot{Z}_i \; [\Omega] \\ \dot{Z}_0 = r_0 + jx_0 = \sum_{i=1}^n r_i + j\sum_{i=1}^n x_i \; [\Omega]$$である。
インピーダンス並列回路の一般式
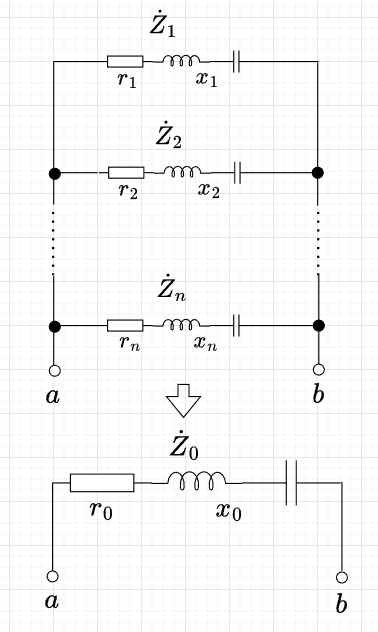
図「インピーダンス並列回路」のように\(n\)個のインピーダンス\(\dot{Z}_1 = r_1 +j x_1 , \; \dot{Z}_2 = r_2 +j x_2 , \; \cdots, \; \dot{Z}_n = r_n +j x_n \)が並列に接続された回路の端子\(a-b\)間に電圧\(\dot{E}\)を加えた時、各インピーダンスに流れる電流を\(\dot{I}_1,\; \dot{I}_2, \;\cdots,\; \dot{I}_n\)とすると、$$\dot{I}_1 = \frac{\dot{E}}{\dot{Z}_1} ,\;\;\; \dot{I}_2= \frac{\dot{E}}{\dot{Z}_2} ,\cdots ,\;\dot{I}_n = \frac{\dot{E}}{\dot{Z}_n} \;[A]$$となる。これらの電流の和が端子\(a-b\)から流入する電流\(\dot{I}\)になるから、$$\dot{I} = \dot{I}_1 + \dot{I}_2 + \cdots + \dot{I}_n = \sum_{i=1}^n \frac{\dot{E}}{\dot{Z}_i} \\= \dot{E} \sum_{i=1}^n \frac{1}{\dot{Z}} \;[A]$$である。従って、等価インピーダンスは、$$\dot{Z}_0 = \frac{\dot{E}}{\dot{I}} = \frac{1}{\sum_{i=1}^n \frac{1}{\dot{Z}_i} }\; [\Omega]$$となる。
ここで、\(n\)個のアドミタンスを$$\dot{Y}_1 = \frac{1}{\dot{Z}_1}, \;\;\; \dot{Y}_2 = \frac{1}{\dot{Z}_2},\;\cdots,\;\dot{Y}_n = \frac{1}{\dot{Z}_n}$$とすると、等価アドミタンスは、$$\dot{Y}_0 = \sum_{i=1}^n \dot{Y}_i \; [S]$$となる。

