13. モード展開と伝達関数行列

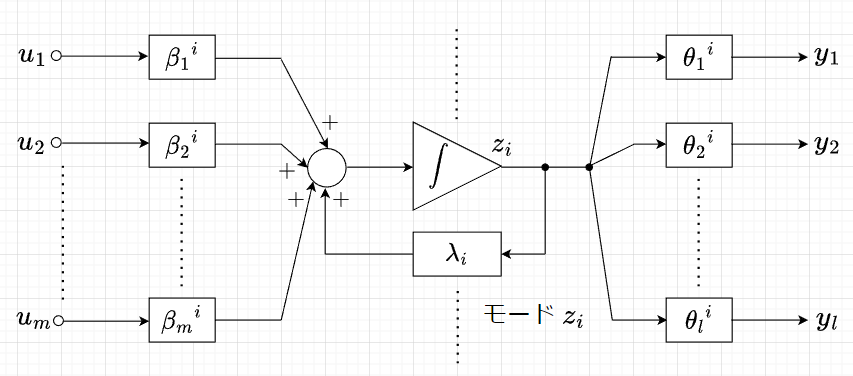
MIMOシステムを対角変換したとき、$$\boldsymbol{\tilde{B} }= \boldsymbol{T}^{-1}\boldsymbol{B} = \begin{bmatrix} \boldsymbol{\beta}^1 \\ \hline \\ \boldsymbol{\beta}^2 \\ \hline \\ \vdots \\ \hline \\ \boldsymbol{\beta}^n \end{bmatrix} , \;\;\;\;\; \boldsymbol{\tilde{C}} = \boldsymbol{CT} = \begin{bmatrix} \boldsymbol{\theta}^1 & | & \boldsymbol{\theta}^2 & | & \cdots & | \boldsymbol{\theta}^n \end{bmatrix}$$となったとすると、\(\boldsymbol{\beta}^i\)と\(\boldsymbol{\theta}^i\)はベクトルとなるので、$$\boldsymbol{\beta}^i = \begin{bmatrix} {\beta_1}^i & {\beta_2}^i & \cdots & {\beta_m}^i \end{bmatrix} \;\;\;(1 \times m) ,\;\;\;\;\;\;\;\;\; \boldsymbol{\theta}^i = \begin{bmatrix} {\theta_1}^i \\ {\theta_2}^i \\ \vdots \\ {\theta_l}^i \end{bmatrix} \;\;\; (l \times 1)$$とおける。\(\boldsymbol{\tilde{A}}\)は、$$\boldsymbol{\tilde{A}} = \boldsymbol{\Lambda} = \boldsymbol{T}^{-1} \boldsymbol{AT} = \begin{bmatrix} \lambda_1 & & \boldsymbol{0} & \\ & \lambda_2 & & \\ & & \ddots & \\ & \boldsymbol{0} & & \lambda_n \end{bmatrix}$$である。
\(\boldsymbol{x}(t) = \boldsymbol{Tz}(t)\)による状態変数の変換により、対角正準システムは、$$\dot{z}_i = \lambda_i z_i + \boldsymbol{\beta}^i \boldsymbol{u} \;\;\;\;\; (i = 1 \sim n)\\ \boldsymbol{y} = \boldsymbol{\theta}^1 z_1 + \cdots +\boldsymbol{\theta}^n z_n$$となり、状態変数線図は、図「MIMOの対角正準システム」のようになる。
よって、\(\boldsymbol{A}\)の固有値に重複したものがないとき、可制御であるための必要十分条件は、\(\boldsymbol{\beta}^i \neq \boldsymbol{0} \; (\forall{i}) \)であり、可観測であるための必要十分条件は、\( \boldsymbol{\theta}^i \neq \boldsymbol{0} \; (\forall{i} ) \)である。つまり、各モードがどれかの入力で制御できれば可制御で、どれかの出力で観測できれば可観測である。
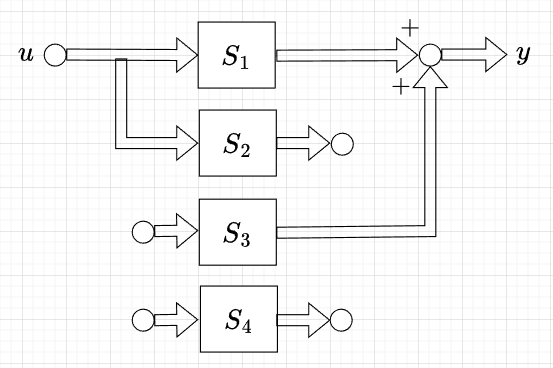
ここで、システムが可制御や可観測でなかったとすると、\(\boldsymbol{\beta}^i = \boldsymbol{0} \)や\( \boldsymbol{\theta}^i = \boldsymbol{0} \)のモードが存在する。従って、システムは、以下の４つのパターンの部分システムに分割できる。
\(S_1 : \; \boldsymbol{\beta}^i \neq \boldsymbol{0} , \; \boldsymbol{\theta}^i \neq 0\)のモード\(z_i\)の集合（可制御、可観測）
\(S_2 : \; \boldsymbol{\beta}^i \neq \boldsymbol{0} , \; \boldsymbol{\theta}^i = 0\)のモード\(z_i\)の集合（可制御、不可観測）
\(S_3 : \; \boldsymbol{\beta}^i = \boldsymbol{0} , \; \boldsymbol{\theta}^i \neq 0\)のモード\(z_i\)の集合（不可制御、可観測）
\(S_4 : \; \boldsymbol{\beta}^i = \boldsymbol{0} , \; \boldsymbol{\theta}^i = 0\)のモード\(z_i\)の集合（不可制御、不可観測）

これは、図「部分システムへの分割」のように表現できる。この図を参考に\(\boldsymbol{u ,\; y}\)間の伝達関数行列を求めると、$$\boldsymbol{G}(s) = \boldsymbol{C}(s \boldsymbol{I} - \boldsymbol{A})^{-1} \boldsymbol{B} = \boldsymbol{\tilde{C}} (s \boldsymbol{I} - \boldsymbol{\tilde{A}})^{-1} \boldsymbol{\tilde{B}}\\ = \sum_{i=1}^n \frac{\boldsymbol{\theta}^i \boldsymbol{\beta}^i }{s - \lambda_i} \\= \sum_{i \in I} \frac{\boldsymbol{\theta}^i \boldsymbol{\beta}^i }{s - \lambda_i}$$ （\(I\)は\(\boldsymbol{\beta}^i \neq \boldsymbol{0},\; \boldsymbol{\theta}^i \neq \boldsymbol{0}\) の\(i\)の集合）

となり、部分システム\(S_2,\;S_3,\;S_4\)の伝達関数行列への寄与は無い。つまり、伝達関数行列は、可制御で可観測のシステムしか表現できない。これが、伝達関数法と状態変数法の大きな違いである。