33. 交流ブリッジ回路

交流ブリッジは、一般に可変キャパシタ\(C\)や可変抵抗器\(R\)を調整してブリッジの平衡条件を満足させることにより、コイルのインダクタンス\(L\)やその抵抗\(R\)を測定しようとするものである。従って、複素数を用いて計算する代表的な回路の一つである。直流のブリッジ回路については、こちらを参照。

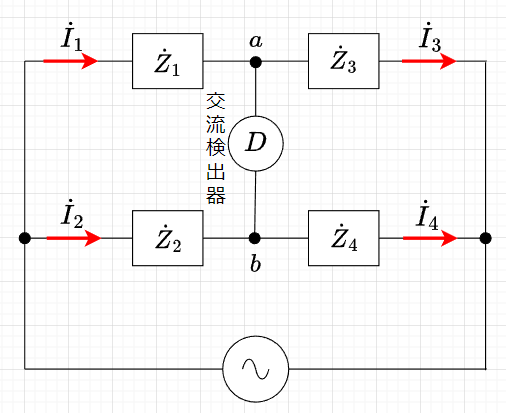
図「交流ブリッジ」の回路で、端子\(a-b\)間の電圧\(\dot{V}_{ab}\)は、$$V_{ab} = \dot{Z}_1 \dot{I}_1 - \dot{Z}_2 \dot{I}_2 = \dot{Z}_3 \dot{I}_3 - \dot{Z}_4 \dot{I}_4 $$となる。このブリッジが平衡して、\(V_{ab} = 0\)　となるためには、$$\dot{Z}_1 \dot{I}_1 - \dot{Z}_2 \dot{I}_2 = \dot{Z}_3 \dot{I}_3 - \dot{Z}_4 \dot{I}_4 = 0 $$が成り立てばよい。

従って、$$\dot{Z}_1 \dot{I}_1 = \dot{Z}_2 \dot{I}_2, \;\;\;\ \dot{Z}_3 \dot{I}_3 = \dot{Z}_4 \dot{I}_4$$なので、$$\frac{\dot{Z}_1 \dot{I}_1 }{\dot{Z}_3 \dot{I}_3} = \frac{ \dot{Z}_2 \dot{I}_2}{\dot{Z}_4 \dot{I}_4}$$となる。
また、平衡時は、\(\dot{I}_1 = \dot{I}_3 , \; \dot{I}_2 = \dot{I}_4\)であるから、$$\frac{\dot{Z}_1}{\dot{Z}_3} = \frac{ \dot{Z}_2}{\dot{Z}_4}$$よって、$$\dot{Z}_1 \dot{Z}_4 = \dot{Z}_2 \dot{Z}_3$$である。
この交流ブリッジの平衡条件を用いて、四つのインピーダンスのうち、未知のインピーダンスを測定する計測器にインピーダンスブリッジがある。