15. オブザーバの構造

状態フィードバックでは、基本的には全ての状態変数が直接観測可能と仮定しているが、実際にはそのような場合は多くない。このときには、制御入力と測定出力から状態変数を再現すればよい。このような仕組みをオブザーバ、あるいは、状態観測器という。制御対象の状態方程式、出力方程式を、$$\boldsymbol{\dot{x}}(t) = \boldsymbol{Ax}(t) + \boldsymbol{Bu}(t) \;\; :\;\boldsymbol{A}(n \times n), \;\; \boldsymbol{B}(n \times m) \; \cdots (1)\\ \boldsymbol{y}(t) = \boldsymbol{Cx}(t) \;\; :\; \boldsymbol{C}(l \times n) \; \cdots (2)$$とする。測定出力は、\(l\)次元である。それぞれの出力は独立で、\(\mathrm{rank}(\boldsymbol{C}) = l\)で(\(\boldsymbol{C, \; A}\)）は可観測とする。

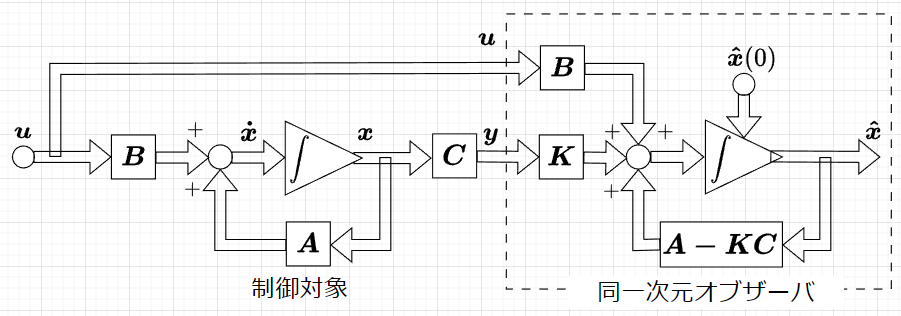
式(1)、式(2)に対して、同一の次元のシステム（同一次元オブザーバ）$$\boldsymbol{\dot{\hat{x}}}(t) = (\boldsymbol{A - KC}) \boldsymbol{\hat{x}} (t)+ \boldsymbol{Ky}(t) + \boldsymbol{B u}(t)\; \cdots (3)$$を制御対象に接続する。（図「同一次元オブザーバ」）ここで、\(\boldsymbol{K} \; (n \times l)\)はゲイン行列と呼ばれ、とくに１出力\((l=1)\)で、\(\boldsymbol{C=c}\;(1 \times n)\)となるときには、\(\boldsymbol{K}\)は列ベクトル\(\boldsymbol{k}\;(n \times 1)\)となり、ゲインベクトルという。
\(\boldsymbol{x}(t)\)と\(\boldsymbol{\hat{x}}(t)\)の誤差ベクトルは、$$\boldsymbol{e} (t) = \boldsymbol{\hat{x}}(t) - \boldsymbol{x}(t)$$となる。これに、式(1),(2),(3)を代入して整理すると、$$ \boldsymbol{\dot{e}}(t) = \boldsymbol{\dot{\hat{x}}}(t) - \boldsymbol{\dot{x}}(t) \\=(\boldsymbol{A-KC})\boldsymbol{\hat{x}}(t) +\boldsymbol{KCx}(t) + \boldsymbol{Bu}(t) - (\boldsymbol{Ax}(t) + \boldsymbol{Bu}(t)) \\=(\boldsymbol{A-KC})(\boldsymbol{\hat{x}}(t) -\boldsymbol{x}(t))$$なので、$$\boldsymbol{\dot{e}}(t) = ( \boldsymbol{A - KC})\boldsymbol{e}(t) \;\;\;\;\;\;\;\boldsymbol{e}(0) = \boldsymbol{\hat{x}}(0) - \boldsymbol{x}(0)$$となる。従って、その解は、$$\boldsymbol{e}(t) = \mathrm{exp}[(\boldsymbol{A - KC})t]\cdot \boldsymbol{e}(0)$$である。この解より、\(\boldsymbol{A - KC}\)　を安定行列にすれば、どんな初期推定誤差\(\boldsymbol{e}(0)\)に対しても、\(t \rightarrow \infty\)　で　\(\boldsymbol{e}(t) \rightarrow \boldsymbol{0}\)、すなわち、\(\boldsymbol{\hat{x}}(t) \rightarrow \boldsymbol{x}(t)\)　となる。ここで、\(\boldsymbol{A - KC}\) の固有値を同一次元オブザーバの極といい、これを複素平面の左半平面のより左側に設定すれば、より速く \(\boldsymbol{\hat{x}}(t) \rightarrow \boldsymbol{x}(t)\) とできる。

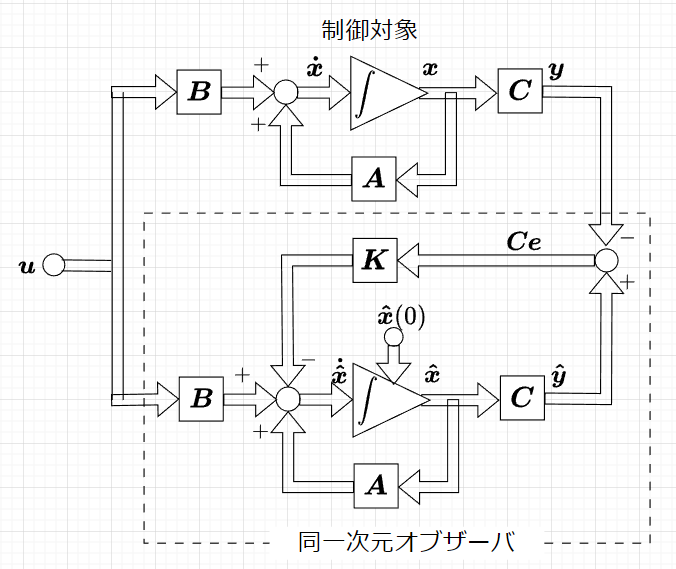
式(3)を変形すると、$$\boldsymbol{\dot{\hat{x}}}(t) = (\boldsymbol{A - KC}) \boldsymbol{\hat{x}}(t) + \boldsymbol{KCx}(t) + \boldsymbol{B u}(t) \\=\boldsymbol{A \hat{x}}(t) + \boldsymbol{Bu}(t) - \boldsymbol{KCe}(t)$$と表せるので、同一次元オブザーバは図「制御対象モデル型の同一次元オブザーバ」のように描ける。この場合、オブザーバは制御対象のモデルと見なすことができる。