35. 三相交流起電力

三相交流発電機は、図「三相交流発電機」に示すように3つのコイルを互いに120度の角度で配置した発電機で、中央の磁石を回転させると、それぞれのコイルに起電力が発生する。コイルに120度の角度があるので、発生する起電力も互いに120度ずれた波形になる。このような関係にある3つの起電力を三相交流起電力と言う。

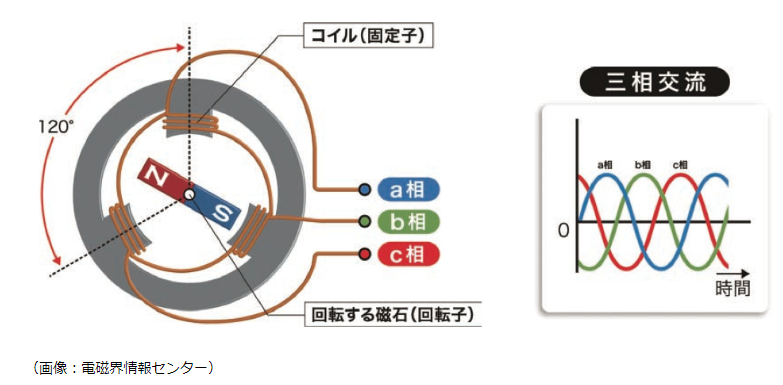
三相交流発電機は、大電力を送れる、送電線の本数が3本で済む、工場などで使う電動機を回す回転磁界が簡単に作れる、などのメリットがあるので、発電によく使われる。 電力会社の発電は三相交流と呼ばれる。
三相交流のメリットは、
・高い電圧で送電することができるので、送電ロスが少ない。
・3つの相の位相差が120度ずつあるので、回転磁界が簡単にできる。
・交流送電なので変圧器で昇圧したり、降圧するのが簡単にできる。
三相交流は、発電所から家庭や工場へ電力を送るのに広く使用されている。また、モータや発電機など、多くの電気機器にも使用されてる。

三相交流の表し方

たがいに\(\frac{2}{3} \pi \;[\mathrm{rad}]\)（120度）ずつ位相差があり、大きさと周波数が等しい3組の交流を対称三相交流（一般に三相交流）という。三相交流に対して一相の交流を用いる場合、単相交流という。
図「三相交流発電機」の各相のコイルの起電力の瞬時値を\(e_a, e_b, e_c\;[V]\)とし、\(e_a\)の初期位相を零とすると、各相の起電力は、$$e_a = E_m \sin \omega t \;[V] \\ e_b = E_m \sin \left(\omega t - \frac{2}{3} \pi\right) \; [V] \\e_c = E_m \sin \left(\omega t - \frac{4}{3} \pi\right) \; [V]$$となる。ここで、\(E_m = \sqrt{2} E\)：振幅で、\(E\)：実効値である。

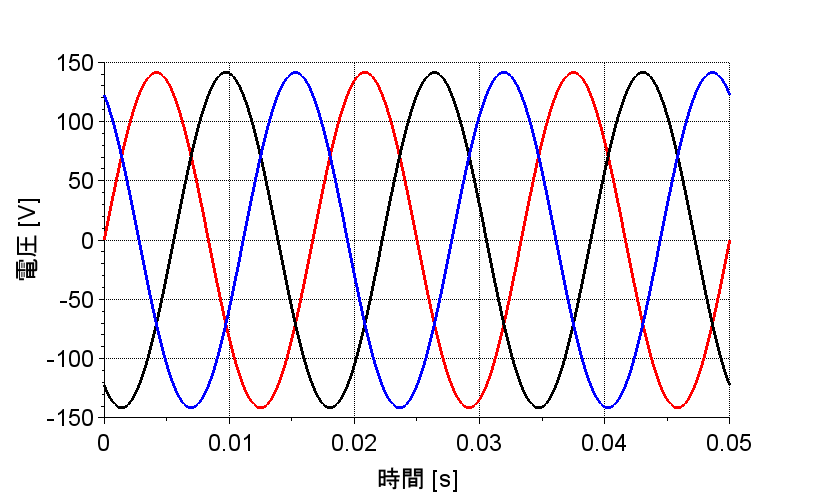
三相交流の波形を図「三相交流の波形」に示す。ここで、起電力を\(\dot{E}_a, \; \dot{E}_b,\; \dot{E}_c \;[V]\)で表すと、三相交流起電力は各相の角周波数が等しいので、\(\omega t\)を省略して表示する。\(\dot{E}_a\)の位相を零として、$$\dot{E}_a = E e^{j0} \; [V] \\ \dot{E}_b = E e^{-j\frac{2}{3} \pi} \;[V]\\ \dot{E}_c = E e^{-j \frac{4}{3} \pi} \;[V]$$となる。ここで、$$\dot{E}_a + \dot{E}_b + \dot{E}_c = E e^{j0} + E e^{-j\frac{2}{3} \pi} + E e^{-j \frac{4}{3} \pi} \\= E + E\left\{ \cos\left(-\frac{2}{3} \pi \right) + j \sin\left(-\frac{2}{3} \pi \right) \right\} + E\left\{ \cos\left(-\frac{4}{3} \pi \right) + j \sin\left(-\frac{4}{3} \pi \right) \right\} \\= E + E\left(-\frac{1}{2} - j\frac{\sqrt{3}}{2}\right) + E\left(-\frac{1}{2} + j\frac{\sqrt{3}}{2} \right) = 0$$となる。つまり、3つの対称三相交流起電力の和は零である。図「三相交流の波形」からも分かる。三相起電力の和が零であることから、三相交流電源を3本の線で負荷と接続できることになる。
図「三相交流の波形」から起電力の位相は、\(e_a \rightarrow e_b \rightarrow e_c\)の順、（赤→黒→青）の順に\(\frac{2}{3}\pi \;[\mathrm{rad}]\)ずつ遅れている。図「三相交流発電機」では、回転子が1秒間に1回転すると、各コイルに1 Hzの起電力が発生する。従って、この発電機で60 Hzの起電力を発生させるには、１分間に回転子を3600回転させなければならない。回転速度を\(N_s\)とすると磁極対数を\(p\)、周波数を\(f\;[Hz]\)として、$$N_s = \frac{60f}{p} \; [\mathrm{rpm}]$$である。\(N_s\)を同期速度という。
日常で使用している電力の周波数（商用周波数）は、富士川以西の西日本では60 Hz、その他の地域では50 Hzである。