36. 三相交流回路の電圧と電流
3相交流回路には、Y結線(スター結線)とΔ結線(デルタ結線)の2つの主要な接続方法がある。これらの結線方法は、3相電力システムでの電力伝送や負荷への接続に使用される。
Y結線は、3つの負荷または電源が中央の接続点で接続される形状をしている。星の形に似ているため、「Y結線」と呼ばれる。Y結線では、各負荷または電源は、他の2つの負荷または電源とも接続される。中央の接続点は、通常はアースに接続される。Y結線は、一般的に低電力の負荷に使用される。
Δ結線は、3つの負荷または電源が三角形の形状で接続される形状をしている。この結線方法は、「デルタ」と呼ばれる。Δ結線では、各負荷または電源は、隣接する2つの負荷または電源と接続される。Δ結線は、一般的に高電力の負荷に使用される。
Y結線とΔ結線
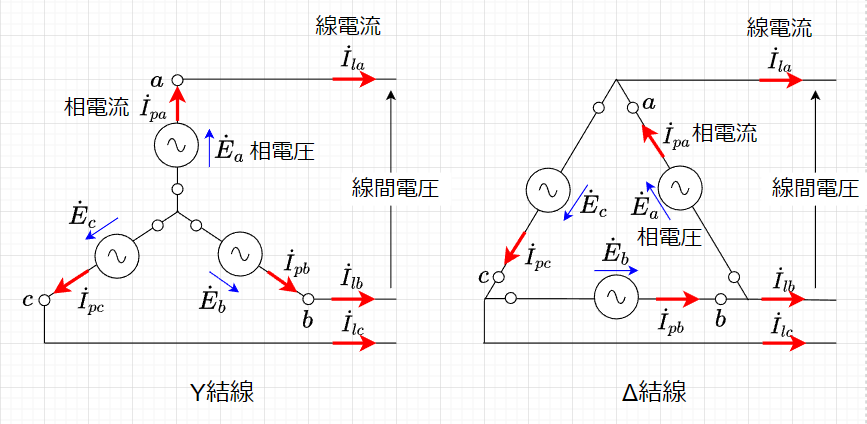
図「電源のY結線とΔ結線」において、図Y結線のようにY形に結線する方法をY結線または星形結線という。また図Δ結線のように△形に結線する方法を、Δ結線または三角結線という。
電源や負荷の一相の電圧、電流をそれぞれ相電圧、相電流という。また、電源と負荷とを接続する線路相互間の電圧を線間電圧、線路に流れる電流を線電流という。
負荷に関しても同様な結線方法がある。図「負荷のY結線とΔ結線」に示す。
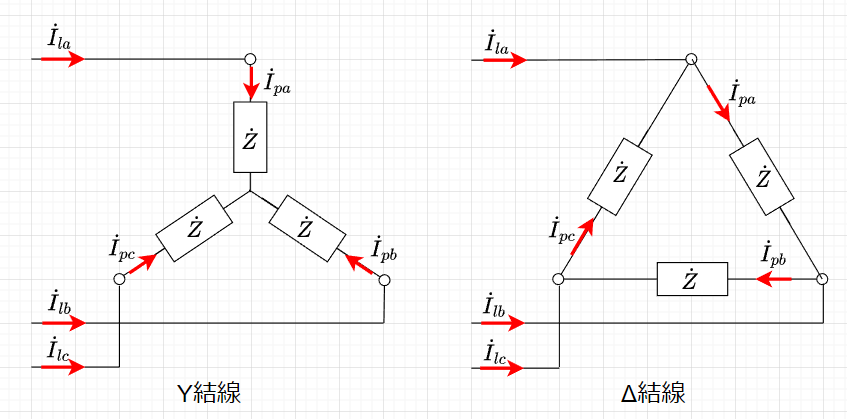
図「負荷のY結線とΔ結線」において、負荷の各相のインピーダンス\(\dot{Z}\)が等しいとき、平衡三相負荷という。通常、三相の負荷は平衡三相負荷とすることが多い。なお、各相のインピーダンスが等しくない負荷を不平衡三相負荷という。
Y結線では、電源および負荷の相電流の和は、\( \dot{I}_{pa} + \dot{I}_{pb} + \dot{I}_{pc} = 0 \)なので、3本の線で電源と負荷を接続できる。Δ結線では、3つの起電力および負荷を環状に結線している。\( \dot{E}_a + \dot{E}_b + \dot{E}_c = 0, \; \; \dot{I}_{pa} + \dot{I}_{pb} + \dot{I}_{pc} = 0 \) であるから、Y結線と同様に、3本の線で電源と負荷を接続できる。
Y結線の電圧、電流
図「YーY結線」では、電源の相電流がそのまま線路に流れるので、線電流と相電流は等しい。$$\dot{I}_{la} = \dot{I}_{pa} , \;\; \dot{I}_{lb} = \dot{I}_{pb} , \;\;\dot{I}_{lc} = \dot{I}_{pc}$$また、線間電圧は、$$\dot{V}_{ab} = \dot{E}_a - \dot{E}_b = Ee^{j0} - Ee^{-j\frac{2}{3}\pi} \\= \sqrt{3}Ee^{j\frac{\pi}{6}} \; [V]$$ $$\dot{V}_{bc} = \dot{E}_b - \dot{E}_c = Ee^{j\frac{2}{3}\pi} - Ee^{-j\frac{4}{3}\pi} \\ = \sqrt{3}Ee^{-j\frac{\pi}{2}} \; [V]$$ $$\dot{V}_{ca} = \dot{E}_c - \dot{E}_a = Ee^{-j\frac{4}{3}\pi} - Ee^{j0} \\ = \sqrt{3}Ee^{-j\frac{7}{6}\pi} \; [V]$$となる。
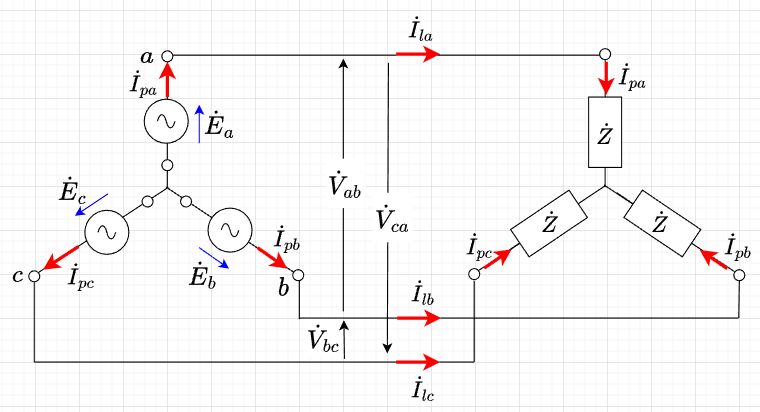
YーY結線での線間電圧、相電圧
Y結線の線間電圧\(V_l\)は、相電圧\(E\)の\(\sqrt{3}\)倍で、\(V_l\)は相対応する\(E\)より\(\frac{\pi}{6}\)[rad] 進み、各\(V_l\)は、互いに\(\frac{2}{3}\pi\)[rad] の位相差がある。
Y結線の相電圧と線間電圧の大きさと位相の例を図「相電圧と線間電圧」に示す。図では、三相のうちの一相分を示している。赤線が相電圧\(\dot{E}_a\)、黒線が線間電圧\(\dot{V}_{ab}\)である。
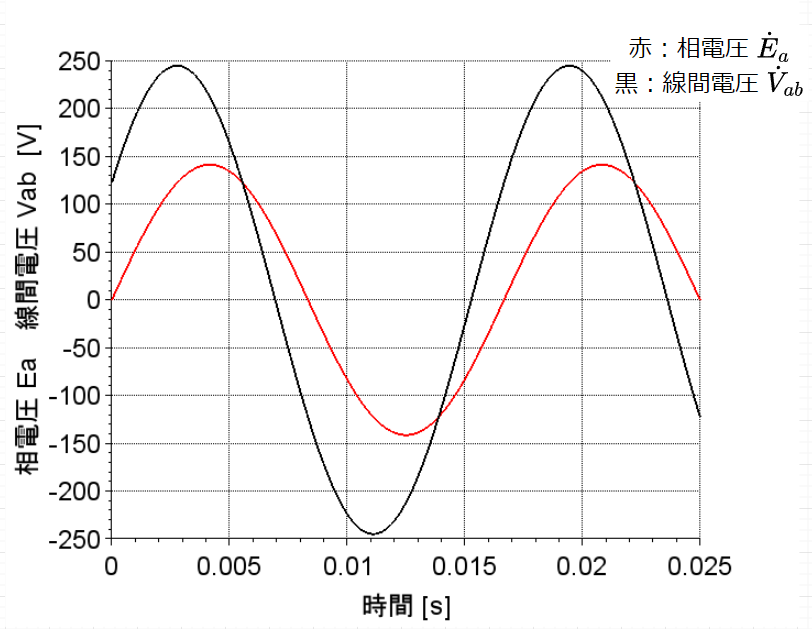
Y結線の相電流および線電流は、$$\dot{I}_{pa} = \dot{I}_{la} = \frac{\dot{E}_a}{\dot{Z}} \;[A]$$ $$\dot{I}_{pb} = \dot{I}_{lb} = \frac{\dot{E}_b}{\dot{Z}} \;[A]$$ $$\dot{I}_{pc} = \dot{I}_{lc} = \frac{\dot{E}_c}{\dot{Z}} \;[A]$$となる。
平衡三相では、相電圧、線間電圧、相電流、線電流、インピーダンスの大きさは各相とも等しい。従って、\(E ,\; V_l , \; I_p ,\; I_l , \; Z\)とすると、$$V_l = \sqrt{3}E \;[V] \\ I_l = I_p = \frac{E}{Z} = \frac{V_l}{\sqrt{3}Z} \; [A]$$と表せる。
負荷の力率を\(\cos \phi \)とすると、負荷で消費される一相の電力\( \hat{P} \)と三相の電力\(P\)は、$$\hat{P} = EI_p \cos\phi \;[W] \\ P=3\hat{P} = 3EI_p \cos\phi = \sqrt{3}V_l I_l \cos\phi \; [W]$$となる。
Δ結線の電圧、電流
図「ΔーΔ結線」では、電源の相電圧がそのまま線間電圧になるので、線間電圧と相電圧は等しい。$$\dot{E}_a = \dot{V}_{ab} , \;\; \dot{E}_b = \dot{V}_{bc} , \;\; \dot{E}_c = \dot{V}_{ca}$$また、相電流は、$$\dot{I}_{pa} = \frac{\dot{E}_a}{\dot{Z}} , \;\; \dot{I}_{pb} = \frac{\dot{E}_b}{\dot{Z}} , \;\; \dot{I}_{pc} = \frac{\dot{E}_c}{\dot{Z}} $$また、負荷の力率を\(\cos \phi\)とすると、線電流は、$$\dot{I}_{la} = \dot{I}_{pa} - \dot{I}_{pc} = Ie^{-j\phi} - Ie^{j(-\phi -\frac{4}{3}\pi)} \\= \sqrt{3}Ie^{j(-\phi - \frac{\pi}{6})}$$ $$\dot{I}_{lb} = \dot{I}_{pb} - \dot{I}_{pa} = Ie^{j(-\phi - \frac{2}{3}\pi)} - Ie^{-j\phi} \\= \sqrt{3}Ie^{j(-\phi - \frac{5}{6}\pi)}$$ $$\dot{I}_{lc} = \dot{I}_{pc} - \dot{I}_{pb} = Ie^{j(-\phi - \frac{4}{3}\pi)} - Ie^{j(-\phi - \frac{2}{3}\pi} \\= \sqrt{3}Ie^{j(-\phi - \frac{9}{6}\pi)}$$ となる。
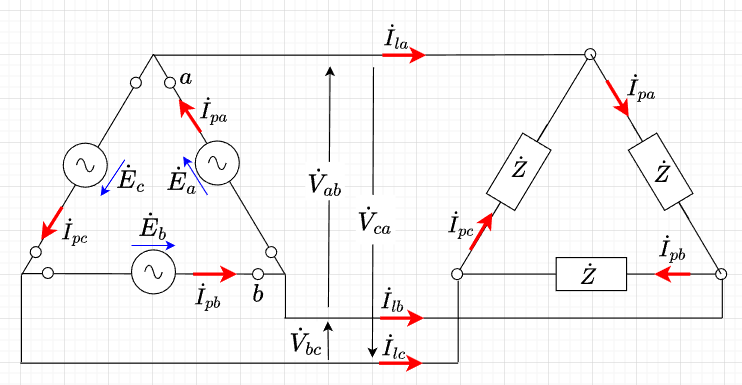
ΔーΔ結線の線電流、相電流
Δ結線の線電流\(I_l\)は相電流\(I_p\)の\(\sqrt{3}\)倍で、\(I_l\)は相対応する\(I_p\)より\(\frac{\pi}{6}\) [rad]遅れ、各\(I_l\)は互いに\(\frac{2}{3}\pi\) [rad] の位相差がある。
平衡三相では、相電圧、線間電圧、相電流、線電流、インピーダンスの大きさは各相とも等しい。従って、\(E ,\; V_l , \; I_p ,\; I_l , \; Z\)とすると、$$V_l = E \;[V] \\I_l = \sqrt{3}I_p = \sqrt{3}\frac{E}{Z} = \sqrt{3}\frac{V_l}{Z} \; [A]$$と表せる。
負荷の力率を\(\cos \phi \)とすると、負荷で消費される一相の電力\( \hat{P} \)と三相の電力\(P\)は、$$\hat{P} = EI_p \cos\phi \;[W] \\ P=3\hat{P} = 3EI_p \cos\phi = \sqrt{3}V_l I_l \cos\phi \;[W]$$となる。


“36. 三相交流回路の電圧と電流” に対して1件のコメントがあります。
コメントは受け付けていません。