37. 負荷インピーダンスのY-Δ変換

電源と負荷の結線法が異なる場合や異なる結線法の負荷が並列になっている場合の回路計算は複雑になる。そこで、電源に影響を与えず、負荷の結線法とインピーダンスの値を等価変換して回路計算を行う。
図「負荷インピーダンスの変換」のように、Y結線とΔ結線の負荷を相互に等価変換する。
変換式は、既に抵抗を使って説明した13. Δ-Y変換、Y-Δ変換の抵抗部分をインピーダンスに置き換えればよい。

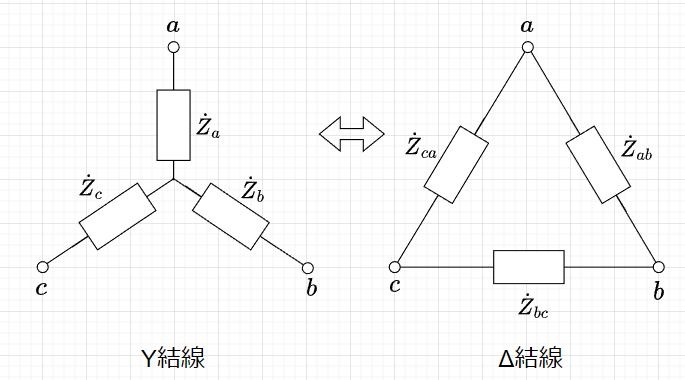
Y結線をΔ結線に変換する式は、$$\dot{Z}_{ab} = \frac{\dot{Z}_\Delta}{\dot{Z}_c}, \;\; \dot{Z}_{bc} = \frac{\dot{Z}_\Delta}{\dot{Z}_a}, \;\; \dot{Z}_{ca} = \frac{\dot{Z}_\Delta}{\dot{Z}_b}$$となる。ここで、$$\dot{Z}_\Delta = \dot{Z}_a \dot{Z}_b + \dot{Z}_b \dot{Z}_c + \dot{Z}_c \dot{Z}_a$$である。
負荷インピーダンスが各相とも等しい平衡三相負荷のときは、\(\dot{Z}_a = \dot{Z}_b = \dot{Z}_c = \dot{Z}\)として、$$\dot{Z}_{ab} = \dot{Z}_{bc} = \dot{Z}_{ca} = \frac{\dot{Z}_\Delta}{\dot{Z}} = \frac{3 \dot{Z}^2}{\dot{Z}} = 3\dot{Z}$$となり、変換後のインピーダンスは変換前の３倍になる。

Δ結線をY結線に変換する式は、$$\dot{Z}_a = \frac{\dot{Z}_{ab} \dot{Z}_{ca}}{\dot{Z}_Y} , \;\; \dot{Z}_b= \frac{\dot{Z}_{bc} \dot{Z}_{ab}}{\dot{Z}_Y} , \;\; \dot{Z}_c = \frac{\dot{Z}_{ca} \dot{Z}_{bc}}{\dot{Z}_Y}$$となる。ここで、$$\dot{Z}_Y = \dot{Z}_{ab} + \dot{Z}_{bc} + \dot{Z}_{ca}$$である。
負荷インピーダンスが各相とも等しい平衡三相負荷のときは、\(\dot{Z}_{ab} = \dot{Z}_{bc} = \dot{Z}_{ca} = \dot{Z}\)として、$$\dot{Z}_a = \dot{Z}_b = \dot{Z}_c = \frac{\dot{Z}^2}{\dot{Z}_Y} = \frac{\dot{Z}^2}{3\dot{Z}} = \frac{\dot{Z}}{3}$$となり、変換後のインピーダンスは変換前の1/3になる。