38. ひずみ波交流
ひずみ波交流は、正弦波ではない交流電圧・電流のことで、正弦波ではない波形をひずみ波といい、このような波形の交流電圧・電流をひずみ波交流と呼ぶ。
例えば、ダイオードや鉄心入りコイルに流れる電流はひずみ波交流となることがある。これらの素子は、いずれも非線形素子で、電圧と電流が比例しない関係をもつことから起こる現象である。
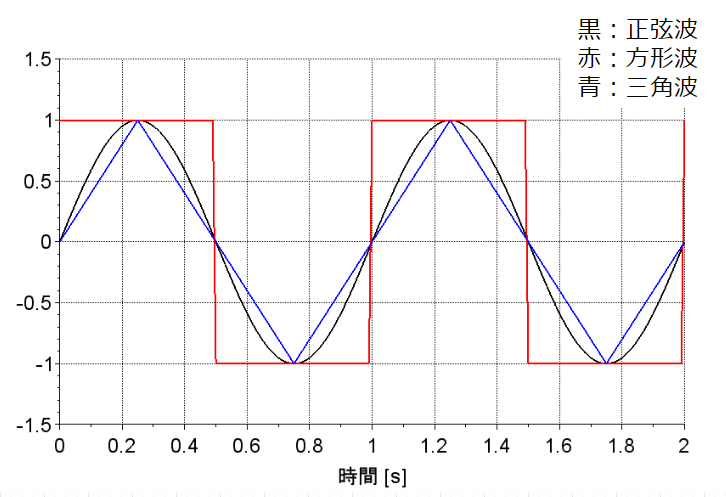
図「正弦波とひずみ波」にひずみ波の例を示す。方形波、三角波はひずみ波と呼ばれる。
正弦波交流の合成
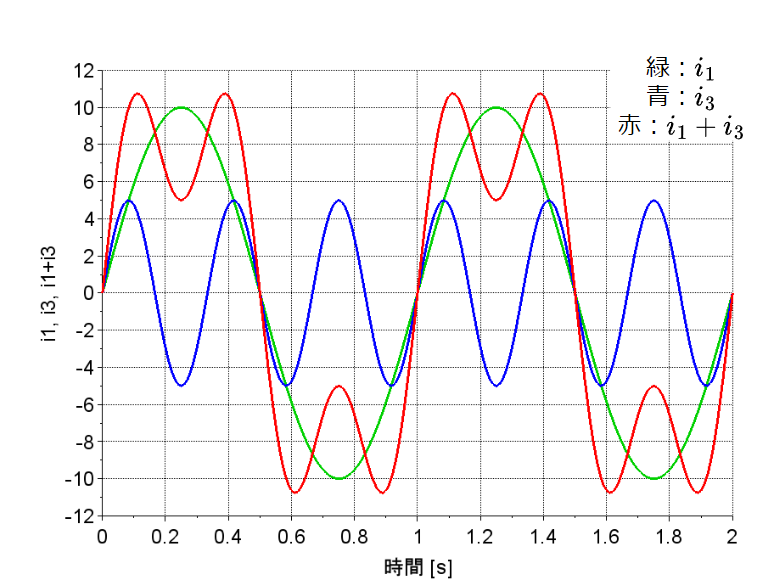
図「正弦波交流の合成(対称波)」のように、ある周波数の正弦波交流\(i_1\)(緑)に対して、3倍の周波数を持つ正弦波交流\(i_3\)(青)を各瞬時値ごとに合成すると、非正弦波交流(赤)となる。これは、時間軸に対して対称波になる。$$i_1=10\sin \omega t \\ i_3 = 5\sin 3\omega t \\ i = i_1 + i_3$$
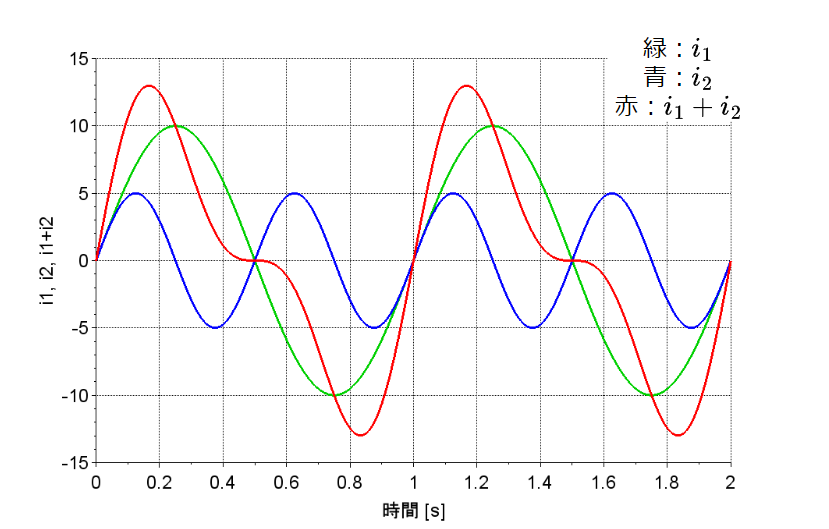
図「正弦波交流の合成(非対称波)」では、\(i_1\)(緑)に対して、2倍の周波数を持つ正弦波交流\(i_2\)(青)を各瞬時値ごとに合成する。この場合も、合成波は非正弦波交流(赤)であるが、これは時間軸に対して非対称となり、非正弦波交流の非対称波となる。$$i_1=10\sin \omega t \\ i_2 = 5\sin 2\omega t \\ i = i_1 + i_2$$
このように、周波数、位相、振幅の異なる正弦波交流を合成すると、いろいろな波形の非正弦波交流が得られる。つまり、非正弦波交流は、周波数などが異なったいくつかの正弦波交流に分解することができる。
一般に、非正弦波交流は、無限級数(フーリエ級数)で表すことができる。$$i = I_0 + A_1 \sin \omega t + A_2 \sin 2 \omega t + A_3 \sin 3 \omega t + \cdots +A_n \sin n \omega t + \cdots \\ + B_1 \cos \omega t +B_2 \cos 2 \omega t + B_3 \cos 3 \omega t + \cdots + B_n \cos n \omega t + \cdots \\ = I_0 + \sum_{n=1}^{\infty} A_n \sin n \omega t + \sum_{n=1}^{\infty} B_n \cos n \omega t $$さらに、$$A_n \sin n \omega t + B_n \cos n \omega t = \sqrt{{A_n}^2 + {B_n}^2 } \sin( n \omega t + \phi_n) \\ I_n = \sqrt{{A_n}^2 + {B_n}^2 } \;\;\;\; \phi_n = \tan^{-1} \frac{B_n}{A_n} \;\;\; (n = 1,2,3, \cdots)$$と変形できるので、$$i = I_0 + \sqrt{2}I_1 \sin(\omega t + \phi_1) + \sum_{n=2}^{\infty} \sqrt{2} I_n \sin(n \omega t + \phi_n) \;\;\cdots (1)$$と表せる。\(I_0\):直流分、\(\sqrt{2}I_1 \sin(\omega t + \phi_1) \):基本波、\(\sum_{n=2}^{\infty} \sqrt{2} I_n \sin(n \omega t + \phi_n)\):高調波、である。このように、非正弦波は一般に、非正弦波交流 = 直流 + 基本波 + 高調波 と表せる。式(1)において、第1項の\(I_0\)は非正弦波交流の直流分を表す。この項は、正の部分の平均値と負の部分の平均値が等しいとき、零となる。第2項は、非正弦波交流\(i\)と同じ周波数の正弦波であり、基本波という。第3項以下は、基本波の整数倍の周波数を持つ正弦波交流で、高調波という。2倍、3倍、・・・、\(n\)倍のものを、それぞれ第2調波、第3調波、・・・、第\(n\)調波という。高調波のうち周波数が基本波の奇数倍のものを奇数調波、偶数倍のものを偶数調波という。
非正弦波交流の実効値、ひずみ率、波形率、波高率
実効値
非正弦波交流の実効値は、直流分、基本波、および各調波の実効値の2乗の和の平方根で表せる。電流の場合、直流分の電流値を\(I_0\)、基本波の電流の実効値を\(I_1\)、各調波の実効値を、\(I_2, I_3,\cdots ,I_n\)とすると、非正弦波交流の実効値は、$$I = \sqrt{{I_0}^2 + {I_1}^2 + {I_2}^2 + \cdots + {I_n}^2} \;[A]$$となる。 同様に、非正弦波交流電圧の実効値は、$$V = \sqrt{{V_0}^2 + {V_1}^2 + {V_2}^2 + \cdots + {V_n}^2} \;[V]$$となる。
ひずみ率
非正弦波交流が正弦波交流に対して、どの程度ひずんでいるか示す指標として、ひずみ率\(k\)を用いる。これは、非正弦波のうち、基本波に対して高調波が含まれる割合で示す。$$k = \frac{\sqrt{{I_2}^2 + {I_3}^2 + \cdots + {I_n}^2}}{I_1} \;\;\;\;\;\; k = \frac{\sqrt{{V_2}^2 + {V_3}^2 + \cdots + {V_n}^2}}{V_1} $$\(k\)の値が、小さいほど正弦波に近くなる。
波形率、波高率
非正弦波交流が正弦波交流からひずんでいる度合いを知る目安として、波形率、波高率がある。これらは、最大値、実効値、平均値を用いて、$$波形率= \frac{実効値}{平均値} , \;\;\;\;\;\; 波高率=\frac{最大値}{実効値}$$と表す。
波形率は、波形の滑らかさを表し、波高率は波形の鋭さを反映する。

