17. オブザーバ併合型状態フィードバック

オブザーバ併合型状態フィードバック制御システムは、オブザーバと状態フィードバックを組み合わせた制御システムである。オブザーバは、直接観測できない状態変数を推定するために使用され、状態フィードバックは、推定された状態変数を基にシステムの出力を制御するために使用される。
オブザーバは、システムの状態方程式と観測方程式に基づいて設計される。状態方程式は、システムの状態変数の時間変化を表し、観測方程式は、観測値が状態変数からどのように計算されるかを表す。オブザーバは、観測値と状態方程式を使用して、直接観測できない状態変数を推定する。
状態フィードバックは、システムの出力とオブザーバによって推定された状態変数を使用して、システムの出力を所望の値に制御するように設計する。
オブザーバ併合型状態フィードバック制御システムは、ロボット工学、航空宇宙工学、その他の制御アプリケーションで使用される。

オブザーバ併合レギュレータ

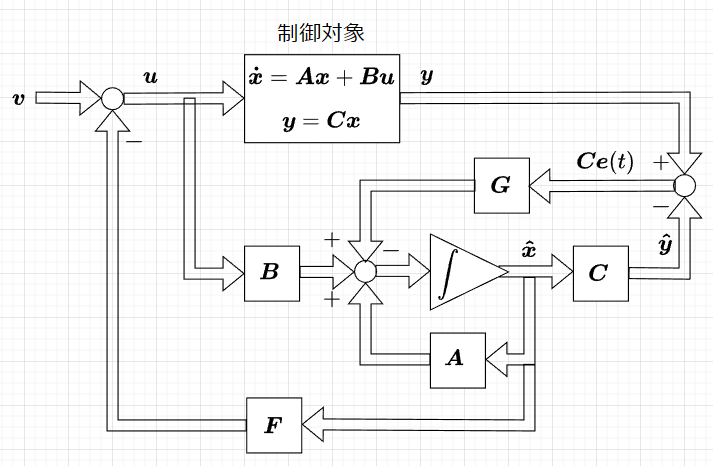
状態フィードバックによるレギュレータを設計する際、状態変数\(\boldsymbol{x}(t)\)が直接測定できない場合、\(\boldsymbol{\hat{x}}(t)\)をオブザーバによって推定して、状態フィードバックを適用すれば良い。図「オブザーバ併合レギュレータシステム」にその構成図を示す。制御対象は、式(1)で、\(\boldsymbol{(A,B)}\)は可制御とする。$$\boldsymbol{\dot{x}}(t) = \boldsymbol{Ax}(t) + \boldsymbol{Bu}(t) \;\;: \boldsymbol{A}(n \times n),\; \boldsymbol{B}(n \times m) \cdots \cdots (1)$$測定出力は、式(2)で、\(\boldsymbol{(C,A)}\)は可観測とする。$$\boldsymbol{y}(t) = \boldsymbol{Cx}(t) \;\; : \boldsymbol{C}(l \times n) \cdots \cdots(2)$$ また、このシステムの同一次元オブザーバ部分を式(3)とする。$$\boldsymbol{\dot{\hat{x}}} = \boldsymbol{A \hat{x}} + \boldsymbol{Bu} + \boldsymbol{G(y - \hat{y})} \\ \boldsymbol{\hat{y}} = \boldsymbol{C \hat{x}} \cdots \cdots (3)$$ とし、状態変数の推定値\(\boldsymbol{\hat{x}}\)に対する状態フィードバック制御則を適用する。$$\boldsymbol{u} = - \boldsymbol{F \hat{x}} + \boldsymbol{v}$$この閉ループ系の安定性を調べる。閉ループ系の状態方程式は、式(4)となる。$$\begin{bmatrix} \boldsymbol{\dot{x}} \\ \boldsymbol{\dot{\hat{x}}} \end{bmatrix} = \begin{bmatrix} \boldsymbol{A} & -\boldsymbol{BF} \\ \boldsymbol{GC} & \boldsymbol{A - BF- GC} \end{bmatrix} \begin{bmatrix} \boldsymbol{x} \\ \boldsymbol{\hat{x}} \end{bmatrix} + \begin{bmatrix} \boldsymbol{B} \\ \boldsymbol{B} \end{bmatrix} \boldsymbol{v} \cdots \cdots (4)$$誤差ベクトル\(\boldsymbol{e = x - \hat{x}}\)を用いて、状態変数を式(5)のように変換する。$$\begin{bmatrix} \boldsymbol{x} \\ \boldsymbol{e} \end{bmatrix} = \begin{bmatrix} \boldsymbol{x} \\ \boldsymbol{x - \hat{x}} \end{bmatrix} = \boldsymbol{T} \begin{bmatrix} \boldsymbol{x} \\ \boldsymbol{\hat{x}} \end{bmatrix} , \;\; \boldsymbol{T} = \begin{bmatrix} \boldsymbol{I} & \boldsymbol{0} \\ \boldsymbol{I} & -\boldsymbol{I} \end{bmatrix} \cdots \cdots (5)$$これにより、式(4)を変換すると、$$\begin{bmatrix} \boldsymbol{\dot{x}} \\ \boldsymbol{\dot{e}} \end{bmatrix} = \boldsymbol{T} \begin{bmatrix} \boldsymbol{A} & -\boldsymbol{BF} \\ \boldsymbol{GC} & \boldsymbol{A - BF -GC } \end{bmatrix} \boldsymbol{T}^{-1} \begin{bmatrix} \boldsymbol{x} \\ \boldsymbol{e} \end{bmatrix} + \boldsymbol{T} \begin{bmatrix} \boldsymbol{B} \\ \boldsymbol{B} \end{bmatrix} \boldsymbol{v} \\= \begin{bmatrix} \boldsymbol{A - BF} & \boldsymbol{BF} \\ \boldsymbol{0} & \boldsymbol{A - GC} \end{bmatrix} \begin{bmatrix} \boldsymbol{x} \\ \boldsymbol{e} \end{bmatrix} + \begin{bmatrix} \boldsymbol{B} \\ \boldsymbol{0} \end{bmatrix} \boldsymbol{v} \cdots \cdots (6)$$となる。この特性多項式は、$$\begin{vmatrix} s\boldsymbol{I - A + BF} & -\boldsymbol{BF} \\ \boldsymbol{0} & s\boldsymbol{I - A + GC} \end{vmatrix} = \begin{vmatrix} s\boldsymbol{I -A +BF} \end{vmatrix} \begin{vmatrix} s\boldsymbol{I - A + GC} \end{vmatrix} \cdots \cdots (7)$$となる。この式(7)からわかるように、同一次元オブザーバを用いた状態フィードバック制御による閉ループシステムの極は、状態フィードバック制御系の閉ループ極と同一次元オブザーバの極からなる。従って、この2種類の系が安定であれば、併合システムも安定である。また、式(7)は、状態フィードバック制御系の極と同一次元オブザーバの極を独立に任意に設定することができる。
一般にオブザーバゲインを設計する際、フィードバックの設計で設定する閉ループ極よりオブザーバの極がより複素平面の左半平面になるようにする。これは、一般に、オブザーバによる状態の推定が、フィードバックによる状態の収束より速いことが必要であるからである。

オブザーバ併合レギュレータの設計【例】

制御対象を$$\boldsymbol{\dot{x}} = \begin{bmatrix} 0 & 1 \\ 0 & -1 \end{bmatrix} \boldsymbol{x} + \begin{bmatrix} 0 \\1 \end{bmatrix} u\\ \boldsymbol{y} = \begin{bmatrix} 1 & 0 \end{bmatrix} \boldsymbol{x}$$とする。 オブザーバの極を\([-3 ,\;-4]\)、また、状態フィードバックの極を\([-1.5 \pm 1.5j]\)に配置する。
Scilabのスクリプト例を示す。可観測性、可制御性をチェックし、オブザーバの極、状態フィードバックの極を設定し、オブザーバゲイン、状態フィードバックゲインを計算する。オブザーバ併合レギュレータは、式(6)に従って構成する。

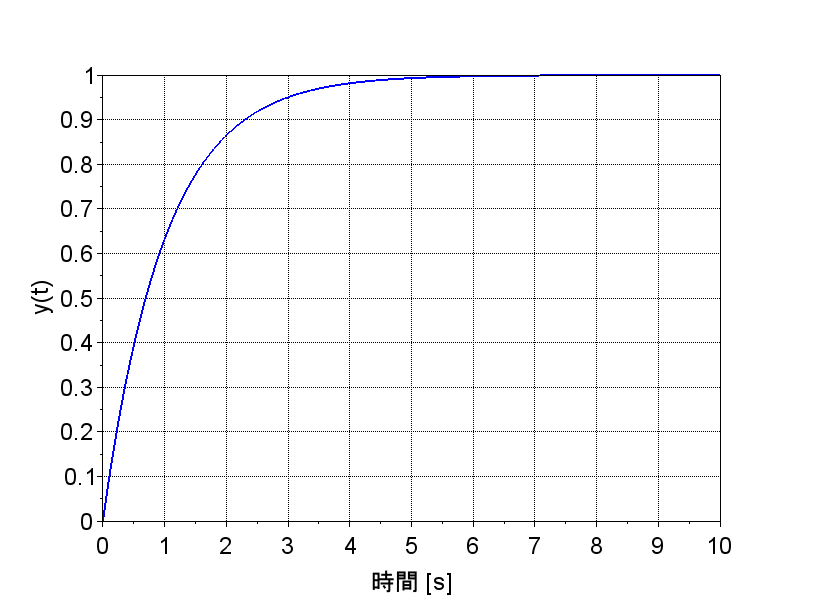
図「制御対象のインパルス応答」から、制御対象はインパルス入力に対して、定常偏差を持つ安定限界にある。ちなみに制御対象の極は、\([0 , -1]\)である。
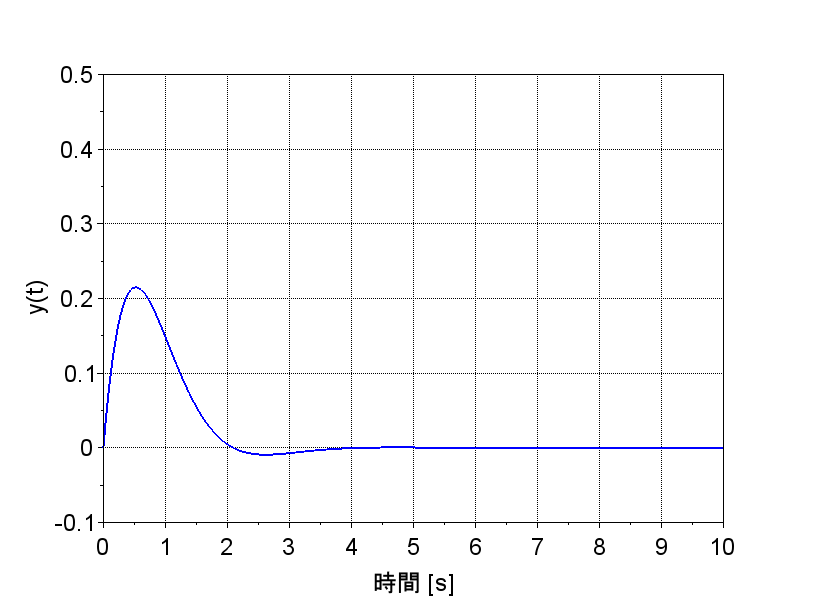
図「オブザーバ併合レギュレータのインパルス応答」では、インパルス応答は、速やかに零に収束している。このことから、オブザーバを用いた状態フィードバックにより、安定なシステムを構成できることがわかる。

Scilabスクリプト
（オブザーバ併合レギュレータの設計）

//オブザーバ併合型状態フィードバック（レギュレータ）
clear;clf();i=%i;
//制御対象
A=[0 1 ; 0 -1];
B=[0 ; 1];
C=[1 0];
P=syslin('c',A,B,C);
//可観測性のチェック
Ob=obsv_mat(A,C);
n=rank(Ob);
//オブザーバの極
ob_poles=[-3 -4];
//オブザーバゲインの計算
G=ppol(A',C',ob_poles);
G=G';
//可制御性のチェック
Cb=cont_mat(A,B);
n2=rank(Cb);
//状態フィードバックの極
f_poles=[-1.5+1.5*i -1.5-1.5*i];
//フィードバックゲインの計算
F=ppol(A,B,f_poles);
//併合システム
Z=[0 0 ; 0 0];
Z2=[0 ; 0];
Z3=[0 0];
Ac=[A-B*F B*F ; Z A-G*C];
Bc=[B ; Z2];
Cc=[C Z3];
P2=syslin('c',Ac,Bc,Cc);
//インパルス応答の計算
t=0:0.01:10;
//制御対象のインパルス応答
y0=csim('impulse',t,P);
scf(0);
plot(t',y0');
//併合システムのインパルス応答
y=csim('impulse',t,P2);
scf(1);
plot(t',y');