40. RLC回路の過渡応答

RLC回路の過渡応答とは、電源が投入された直後、回路の電流が定常状態に達するまでの時間の経過に伴う電圧と電流の変化のことである。RLC回路は、抵抗\(R\)、インダクタンス\(L\)、キャパシタンス\(C\)の3つの要素で構成される回路で、電源が投入されると、回路の電流は\(R,\;L,\;C\)の3つの要素の相互作用によって変化する。\(R\)は電流の流れを妨げ、\(L\)は電流の変化を妨げ、\(C\)は電荷を蓄える。これらの要素の相互作用によって、回路の電流は定常状態に達するまで変化する。
RLC回路の過渡応答は、電気機器の動作に影響を与えることがある。一般に、電気機器は一定の電流や電圧で動作するように設計しており、RLC回路の過渡応答によって、電流や電圧が変化すると、電気機器の動作に異常が発生することがある。そのため、RLC回路の過渡応答を予測し、電気機器の動作に影響を与えないように対策を行う必要がある。

直流電源印可の場合

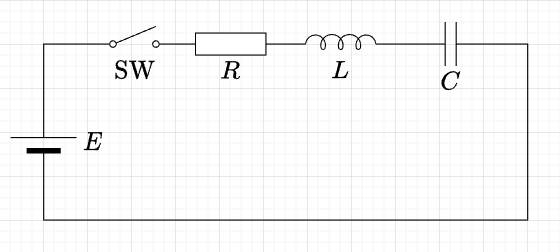
図「RLC回路への直流電源の印可」において、SWをONにした場合の回路方程式は、$$L\frac{di}{dt} + Ri + \frac{1}{C} \int i dt=E$$となる。

ここで、$$e_C = \frac{1}{C} \int i dt = \frac{q}{C} , \;\;\; i=C\frac{de_C}{dt} = \frac{dq}{dt}$$なので、これを代入して、$$LC\frac{d^2e_C}{dt^2} +RC\frac{de_C}{dt} + e_C = E , \;\;\;\;\; L\frac{di}{dt} + Ri +\frac{1}{C}\int i dt = E\cdots\cdots (1)$$この微分方程式を解けば、\(i(t)\)の定常解、過渡解が求まる。詳細は、14. 二次遅れ要素（２次遅れ系）の時間応答を参考にして欲しい。
式(1)を初期値０としてラプラス変換すると、$$LsI(s)+RI(s)+\frac{1}{Cs}I(s)=\frac{E}{s} ,\;\;\;\; \left(Ls^2 + Rs + \frac{1}{C}\right)I(s) = E , \;\;\;\; I(s) =\frac{CE}{LCs^2 + RCs + 1}$$ よって、特性根は$$s = \frac{-RC \pm \sqrt{(RC)^2 - 4LC}}{2LC} = -\frac{R}{2L} \pm \sqrt{\left(\frac{R}{2L}\right)^2 - \frac{1}{LC}}$$となるので、根号内の正、負、零の場合で応答が異なる。（根号内が負の場合は、複素数となる）
ここでは、LTspiceにより、数値解析で時間応答特性を把握する。

LTspiceによる解析

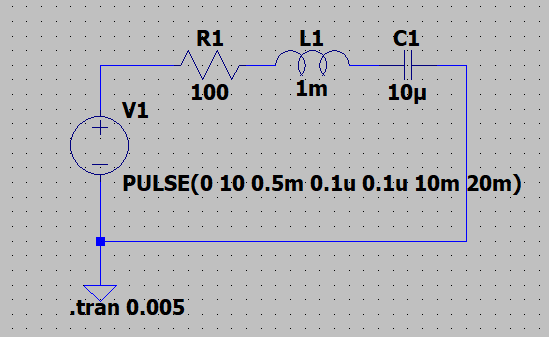
LTspiceを使って図「LCR回路（LTspice)」の回路で過渡特性を求める。
\(R,L,C\)の各パラメータを変えて、時間応答を比較する。
（１）$$\left(\frac{R}{2L}\right)^2 \gt \frac{1}{LC},\;\;\;\;R \gt 2\sqrt{\frac{L}{C}}$$の場合
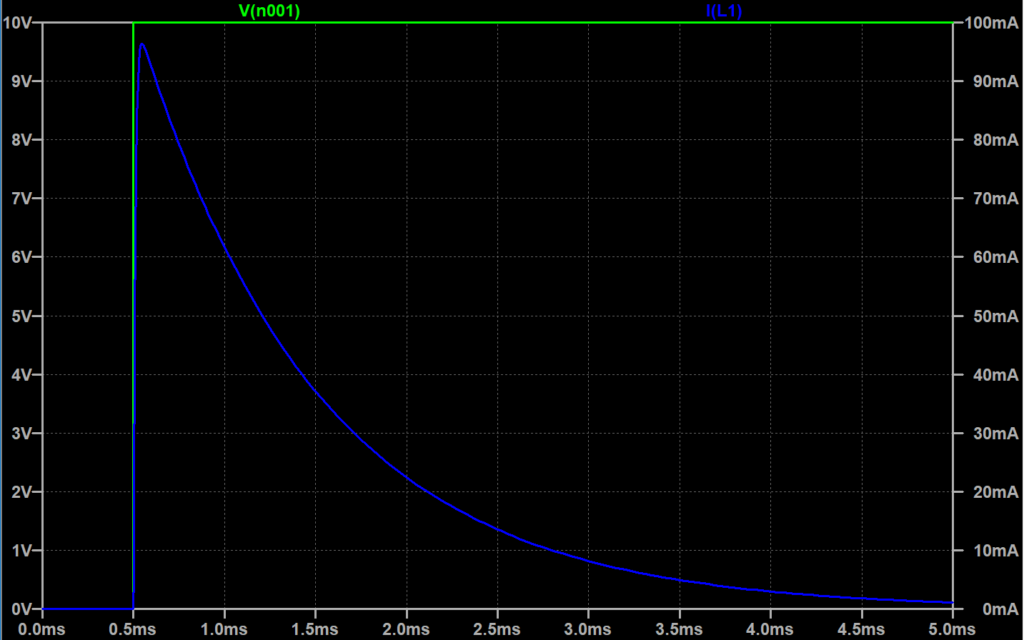
\(R:100 \; \Omega, \;\;L = 1\;mH, \;\; C=10\; \mu F\)
図「(1)の場合」で、緑線が入力電圧（V1）で、青線が電流である。電流は、ある時刻\(\tau\)で最大値になり、以降やるやかに減少して零になる。

（２）$$\left(\frac{R}{2L}\right)^2 = \frac{1}{LC},\;\;\;\;R =2\sqrt{\frac{L}{C}}$$の場合
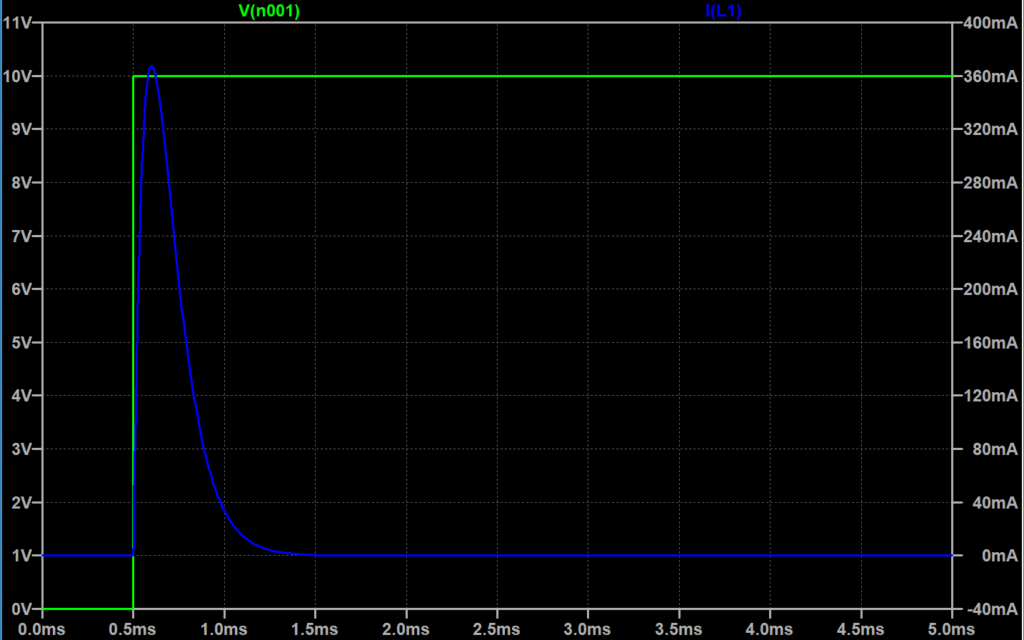
\(R:20 \; \Omega, \;\;L = 1\;mH, \;\; C=10\; \mu F\)
図「(2)の場合」では、電流（青線）は、ある時刻\(\tau\)で最大値になり、非振動的ではあるが、急速に減少して零になる。これは、(1)の場合から(3)の場合への境になり、臨界的な場合である。

（３）$$\left(\frac{R}{2L}\right)^2 \lt \frac{1}{LC},\;\;\;\;R \lt 2\sqrt{\frac{L}{C}}$$の場合
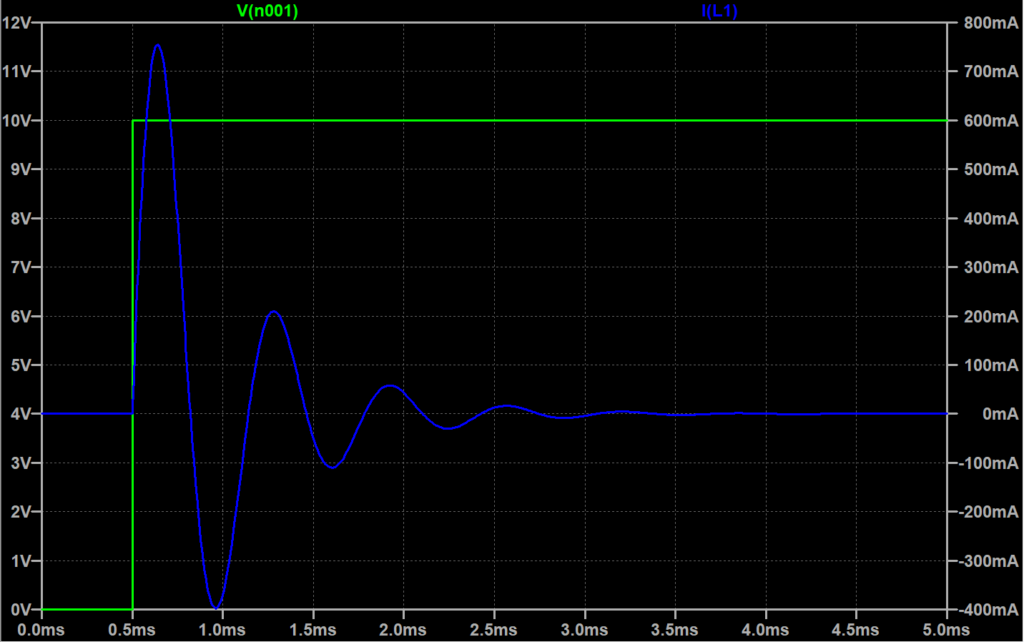
\(R:4 \; \Omega, \;\;L = 1\;mH, \;\; C=10\; \mu F\)
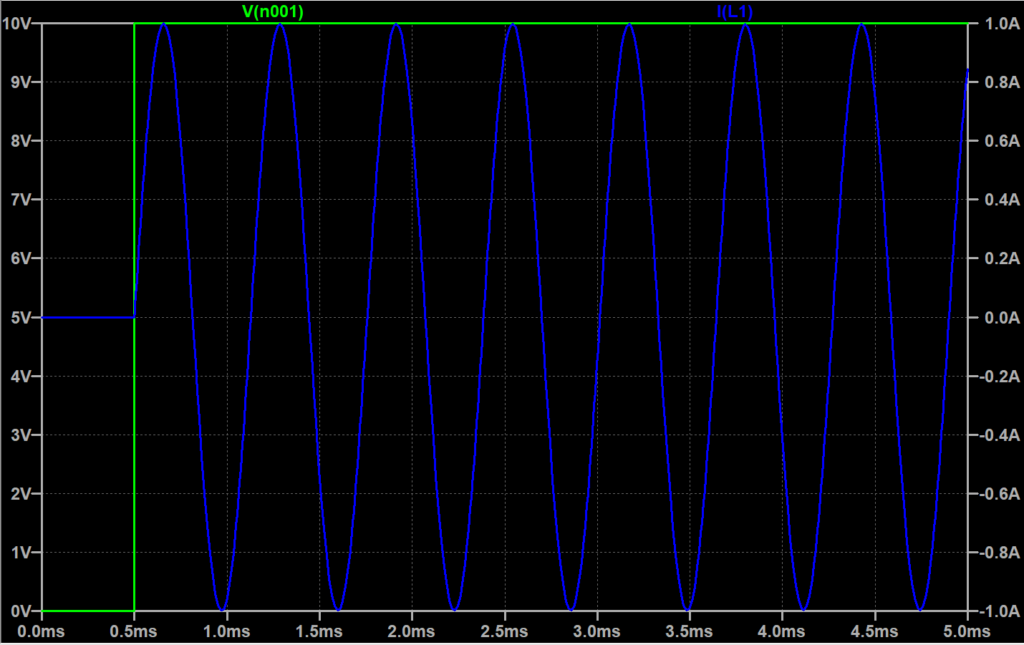
図「(3)の場合」では、電流（青線）は、ある時刻\(\tau\)で最大値になり、その後振動的に減衰し、零になる。この振動周波数\(f\)を固有周波数といい、$$f = \frac{1}{2\pi}\sqrt{\frac{1}{LC}-\left(\frac{R}{2L}\right)^2} \;[Hz]$$となる。
なお、\(R=0\)とすると、図「\(R=0\)の場合」のように電流の振動は減衰しなくなり、$$f = \frac{1}{2\pi}\sqrt{\frac{1}{LC}} \;[Hz]$$の定常振動（この周波数での正弦波）となる。