41. 相互誘導回路の過渡応答

相互誘導の過渡応答では、相互誘導回路において、電源が切断されたときや電流が変化したときに、コイルに流れる電流がどのように変化するかを見る。
相互誘導回路とは、2つのコイルが磁気的に結合している回路で、2つのコイルの相互インダクタンスは、コイルの巻数とコイルの中心間距離に依存する。相互インダクタンスが大きいほど、2つのコイルは磁気的に強く結合している。
電源が切断されたとき、コイルに流れていた電流は磁場として保存される。このため、磁場は2つのコイルに相互作用し、2つのコイルに逆起電力が生じる。この逆起電力は、コイルに電流を流し続け、磁場を維持しようするため、電源が切断された後も、コイルにはしばらく電流が流れ続ける。
電流が変化したときも、同様の現象が起こる。電流が増加すると、磁場が強くなり、逆起電力が増加する。これにより、電流の増加を妨げる。電流が減少すると、磁場が弱くなり、逆起電力も減少する。
相互誘導の過渡応答は、電源の切断、電流の変化、またはコイルの接続/切断によって引き起こされる可能性があるため、変圧器などを使った電気機器や電力制御回路の設計において考慮する必要がある。

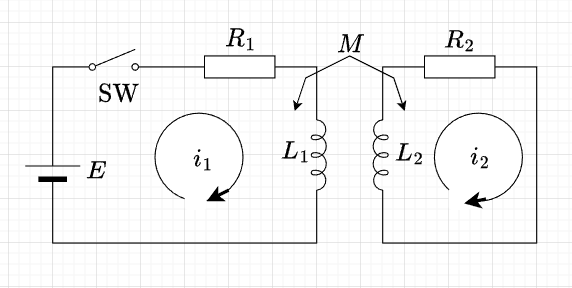
図「相互誘導回路の過渡応答」に示すように、抵抗と自己インダクタンスとの直列回路の二つが相互インダクタンス\(M\)によって結合されている場合、左側の回路に\(t=0\)において直流起電力\(E\)を加える。各回路に流れる電流\(i_1,i_2\)を図のように定めると、次の回路方程式を得る。$$L_1\frac{di_1}{dt} + R_1 i_1 + M\frac{di_2}{dt}=E \\L_2 \frac{di_2}{dt} + R_2 i_2 + M \frac{di_1}{dt}=0$$

この二つの方程式から、\(i_1\)だけの方程式を求めると、$$\frac{d^2 i_1}{dt^2} + \frac{L_1 R_2 + L_2 R_1}{L_1 L_2 - M^2}\frac{di_1}{dt} + \frac{R_1 R_2}{L_1 L_2 - M^2} i_1 = \frac{R_2}{L_1 L_2 -M^2}E$$また、\(i_2\)だけの方程式を求めると、$$\frac{d^2 i_2}{dt^2} + \frac{L_1 R_2 + L_2 R_1}{L_1 L_2 - M^2} \frac{di_2}{dt} + \frac{R_1 R_2}{L_1 L_2 - M^2}i_2 = 0$$となる。\(i_1\)の定常電流は、\(i_1 = E/R_1\)であり、\(i_2\)の定常電流は\(i_2 = 0\)である。これらの微分方程式から、過渡解を求めることで、相互誘導回路の過渡応答を求めることができるが、解は複雑な式となる。これだけの回路であっても過渡応答解を定性的に求めることは容易でない。とはいえ、Maximaなどの数式処理システムを使いこなすことで、効率よく定性解を求めることができる。（電気電子回路、制御工学におけるMaximaの使い方は、改めてまとめる予定である。）

LTspiceによる相互誘導回路の過渡応答

ここでは、LTspiceを使って、相互誘導回路の過渡応答を求める。各素子の具体的な回路定数が必要になるが、実際の回路解析では、各素子が既知であるので、通常、問題ない。また、回路定数を変化させることで、その回路の特性を把握することができる。勿論、定性的な振る舞いを予測して、シミュレーションすることが望ましい。
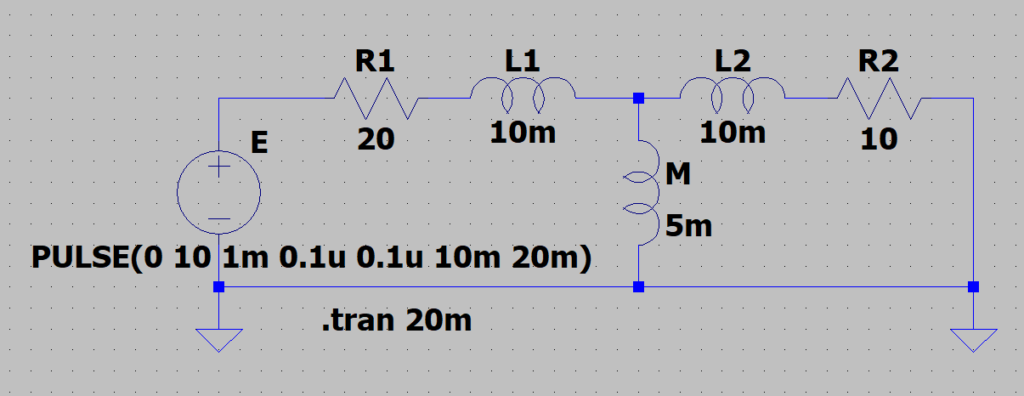
図「相互誘導回路の過渡応答　LTspice」にLTspiceの回路図を示す。各素子の回路定数は、\(R_1=20 \; \Omega ,\; L_1=10\;mH, \\ R_2 =10\; \Omega, \; L_2=10\;mH, \; k=0.5\)（\(k\)は結合係数）とした。

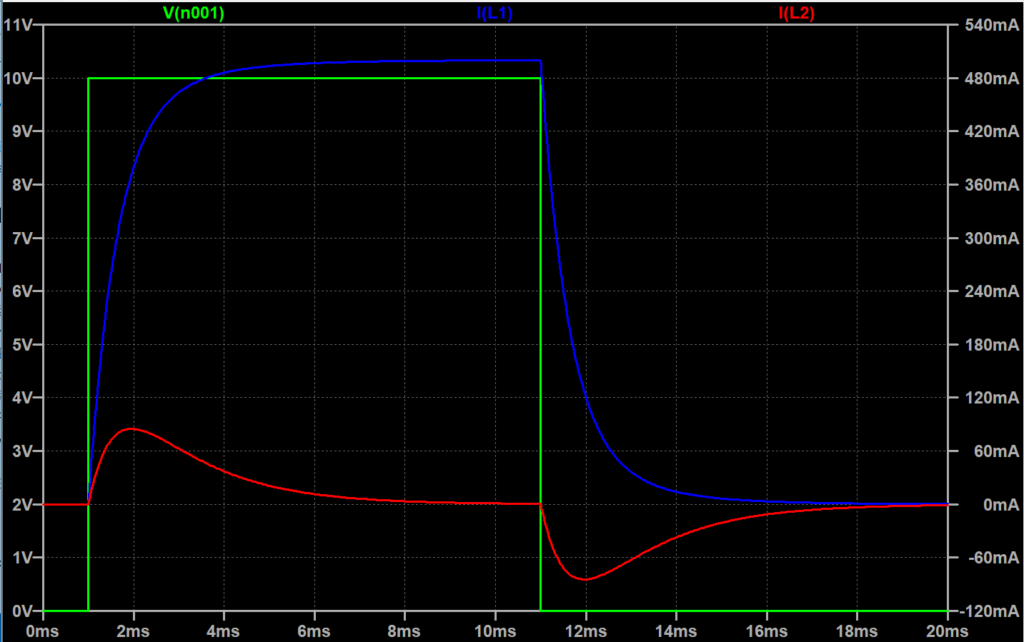
図「過渡応答（シミュレーション）」にシミュレーション結果を示す。緑線が入力電圧\(E\)である。青線が１次側の電流\(i_1\)、赤線が２次側の電流\(i_2\)である。入力電圧\(E\)がステップ状に高くなると、\(i_1\)は、インダクタンス\(L_1\)と抵抗\(R_1\)により、電流が立ち上がるが徐々に電流の増加が緩やかになり、定常値\(i_1 = E/R_1=\frac{10}{20}=500\;mA\)に達する。\(i_2\)は、相互誘導により、始めは電流が増加するが１次側の電流の変化が小さくなるにともない、電流は減少し、\(i_2 = 0 \; A\)になる。入力電圧\(E\)が10Vから０V に変化する場合は、\(i_1\)は定常値から減少するが、減少は徐々に緩やかになる。この１次側電流により、\(i_2\)は始めは負の方向に電流が流れるが１次側の電流の変化が小さくなるにともない、電流は緩やかに\(i_2 = 0 \; A\)に達する。