21. 電圧帰還並列注入形負帰還増幅回路
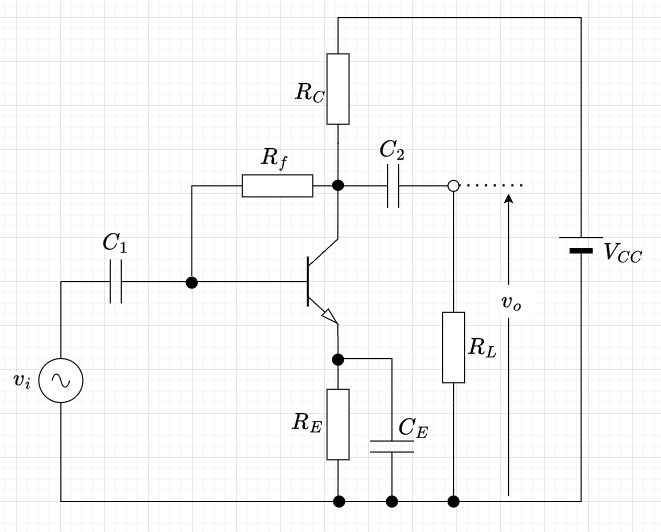
図1に示す電圧帰還並列注入形負帰還増幅回路では、コレクタからベースに\(R_f\)を介して電圧帰還されている。図2の等価回路から、$$(i_f -h_{fe}i_b)\frac{R_C R_L}{R_C + R_L} = i_l R_L \\ i_l = (i_f - h_{fe} i_b) \frac{R_C}{R_C +R_L} = \frac{v_o}{R_L} \\ i_f = \frac{v_i - v_o}{R_f} \approx - \frac{v_o}{R_f} \;\;\;\;( |v_i| < |v_o|)$$である。以上の式から電圧増幅度\(A_{vf}\)を求めると、$$v_o \left(\frac{1}{R_L} + \frac{R_C}{R_f(R_C + R_L)}\right)\\ = -\frac{h_{fe}}{h_{ie}} \frac{R_C}{R_C + R_L} v_i \\ A_{vf} = \frac{v_o}{v_i} = \frac{- \frac{h_{fe}}{h_{ie}} R_{AL}}{ 1 + \frac{R_{AL}}{R_f}} = \frac{A_v}{1 + \beta} \\ R_{AL} = \frac{R_C R_L}{R_C + R_L} \\ \left( A_v = - \frac{h_{fe}}{h_{ie}} R_{AL} , \;\;\;\;\;\; \beta = \frac{R_{AL}}{R_f} \right) $$となる。通常、\(\beta \ll 1\)なので、\(A_{vf} \approx A_{v}\)となり、この回路構成の場合、負帰還を掛けても電圧増幅度は、ほとんど変わらない。
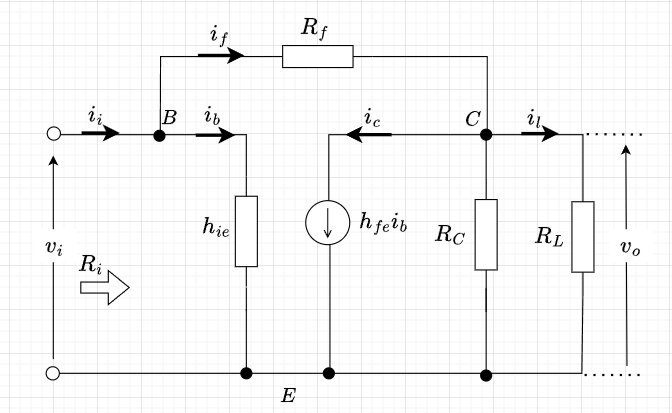
電流増幅度\(A_{if}\)を考える。帰還を掛けない時の電流増幅度\(A_i\)は、$$i_l = -h_{fe} i_b \frac{R_C}{R_C +R_L} \\ \frac{i_l}{i_b} = -h_{fe} \frac{R_C}{R_C +R_L} \\ i_b = i_i \\ A_i = \frac{i_l}{i_i} = \frac{i_l}{i_b} = -h_{fe} \frac{R_C}{R_C + R_L} $$となる。帰還を掛けた時の電流増幅度\(A_{if}\)は、近似的な見積もりでは、$$i_i = i_f + i_b \approx i_f \;\;\;\;(i_b \ll i_f) \\ i_f = \frac{v_i - v_o}{R_f} \approx - \frac{v_o}{R_f} \;\;\;\;( |v_i| < |v_o|) \\ v_o = R_L i_l \;\;\;\;\; i_f \approx - \frac{R_L}{R_f} i_l \;\;\;\;\; i_i \approx -\frac{R_L}{R_f} i_ l\\ A_{if} = \frac{i_l}{i_i} \approx -\frac{R_f}{R_L} $$ となる。
電圧帰還並列注入形負帰還増幅回路(LTspice)
図3は、電圧帰還並列注入形負帰還増幅回路のLTspice用回路図である。
電圧増幅度は、$$A_v = - \frac{h_{fe}}{h_{ie}} R_{AL} \\ R_{AL} = \frac{R_C R_L}{R_C + R_L} \;\;\;\; \beta = \frac{R_{AL}}{R_f} \\ A_{vf} = \frac{A_v}{1 + \beta}$$なので、BJTの2N2222の特性を \(h_{fe} = 75 ,\;\; h_{ie}=1.25\;k\Omega \)とすると、$$A_{vf} \approx A_{v} \approx -130$$となる。
図4は、シミュレーション結果である。入力電圧\(v_i\)は、振幅 5 mV , 周波数 1 kHzの正弦波である。このとき、出力電圧\(v_o\)は、振幅 540 mVで入力電圧\(v_i\)とは逆相となっている。なお、増幅度は約110で、概算値と良い一致を示している。
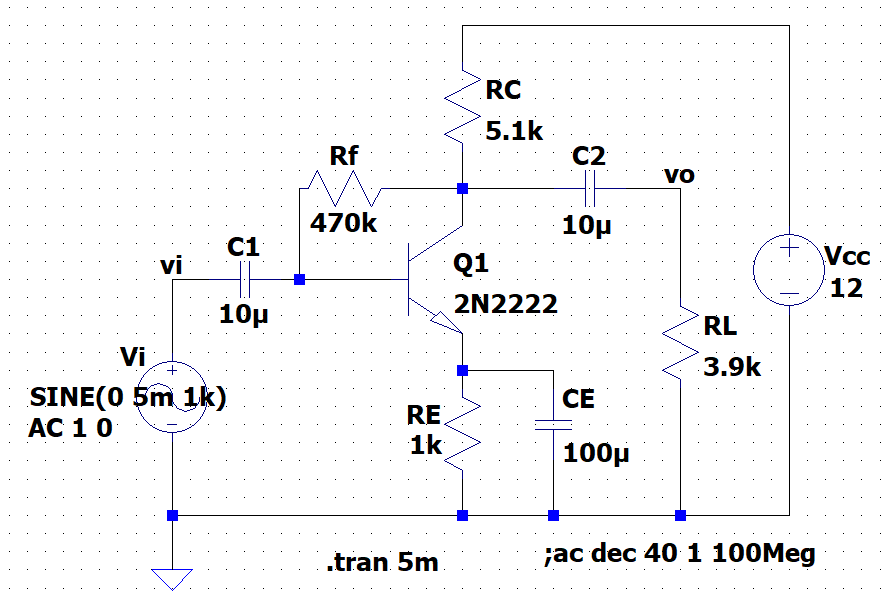
(LTspice)
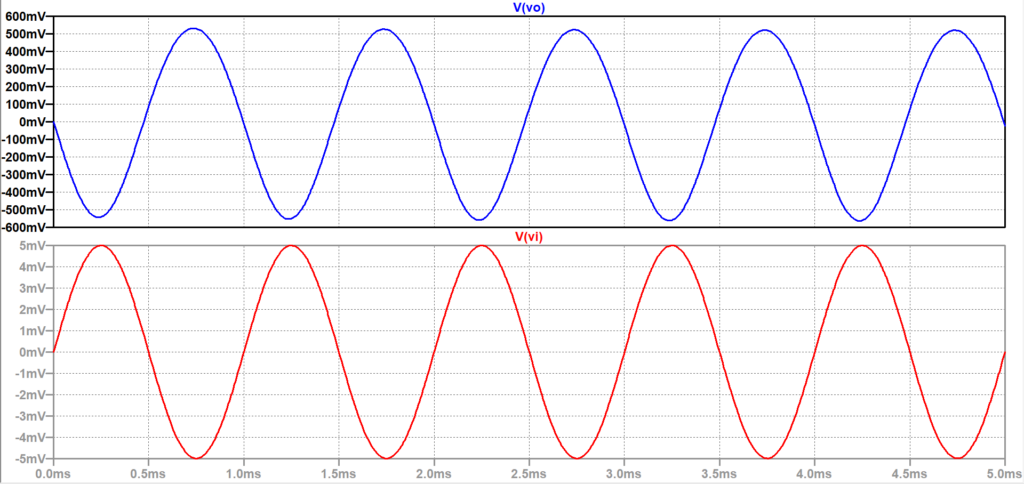
赤:入力\(v_i\) 青:出力\(v_o\)

