28. CR発振回路
CR発振回路は、キャパシタ\(C\)と抵抗\(R\)を組み合わせた発振回路である。この回路は、CR移相回路をフィードバック回路として用いることで、発振を実現する。
CR移相回路
図1「CR移相回路」において、入力と出力間の位相差を考える。図の各\(\dot{I},\;\;\dot{V}\)より、以下の式が成り立つ。なお、入力電圧を\(\dot{V}_i\)、出力電圧を\(\dot{V}_o\)とする。
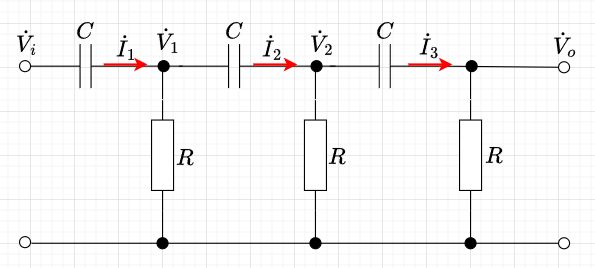
$$\dot{V}_1 = (\dot{I}_1 -\dot{I}_2)R \;\;\;\;\; \dot{V}_2= (\dot{I}_2 -\dot{I}_3)R \\ \dot{V}_o= \dot{I}_3 R $$また、$$\dot{V}_i - \dot{V}_1 = \frac{1}{s C} \dot{I}_1 \\ \dot{V}_1 - \dot{V}_2 = \frac{1}{s C} \dot{I}_2 \\ \dot{V}_2 - \dot{V}_o = \frac{1}{s C} \dot{I}_3$$である。これらの式から\(\dot{I}\)の項を消去し、式を整理すると\(\dot{V}_i\)と\(\dot{V}_o\)間の伝達関数\(G(s)\)は、$$G(s) = \frac{V_o(s)}{V_i(s)} =\frac{s^3 C^3 R^3}{s^3 C^3 R^3 + 6s^2 C^2 R^2 + 5s C R + 1}$$となる。周波数伝達関数を求めるには、\(s \rightarrow j \omega\)とすればよい。従って、$$G(j \omega) = \frac{ - \omega^3 C^3 R^3}{5 \omega C R - \omega^3 C^3 R^3 + j ( 6 \omega^2 C^2 R^2 - 1)}$$ 周波数伝達関数より、入力電圧\(\dot{V}_i\)と出力電圧\(\dot{V}_o\)の位相差が、逆位相(180度)となる角周波数は、分母の虚部が0となるときなので、\(\omega = \frac{1}{\sqrt{6} C R}\)である。従って、周波数\(f\)は、$$f=\frac{1}{2 \pi \sqrt{6} C R}$$ である。
なお、\(CR\)回路1段で変化できる移相量(位相の変化量)は90度未満なので、2段以下では180度位相を変化させることはできない。よって、\(CR\)回路は3段以上必要となる。
CR移相発振回路(LTspice)
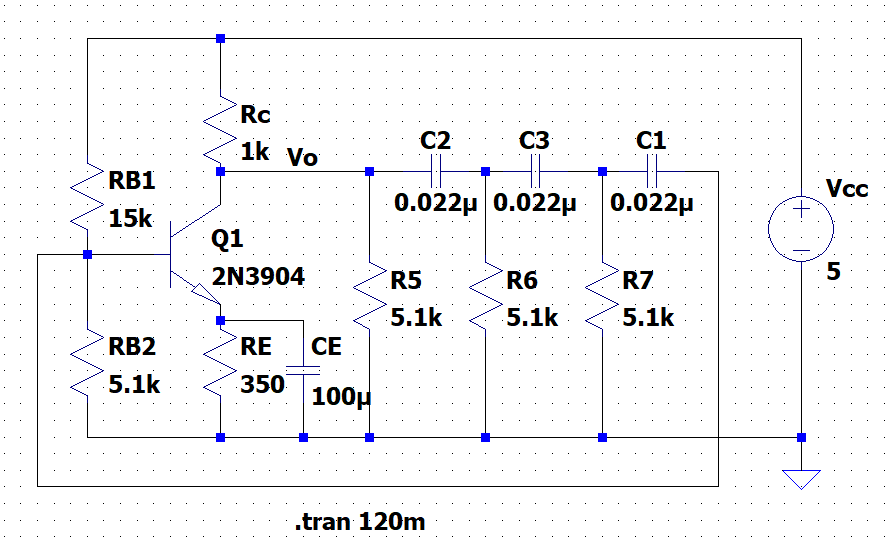
図2はCR移相発振回路のLTspice回路図である。増幅回路はエミッタ接地増幅回路なので、ベース電圧\(v_{be}\)と出力側のコレクタ電圧\(v_{ce}\)は逆相(位相が180度ずれる)となる。CR回路3段で構成された移相回路で、位相が180度ずれるので、結局、基のベース電圧と帰還された電圧は360度位相がずれるので、正帰還となり発振する。
図3がシミュレーション結果で、発振出力のコレクタ電圧\(v_o\)を青線で示す。トランジスタ(Q1)の出力側のコレクタ電流\(I_{R_C}\)(赤線)と入力側のベースへの帰還電流\(I_{C_1}\)(緑線)は逆相となっていることがわかる。
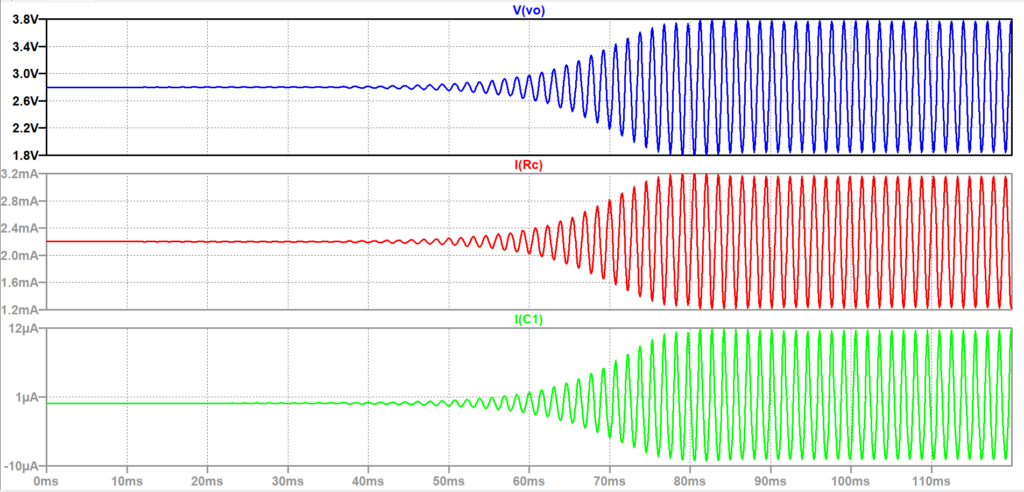
青:出力電圧(コレクタ電圧)\(v_o\)、赤:コレクタ電流\(I_{R_C}\)、緑:ベースへの帰還電流\(I_{C1}\)

