2. 基本論理演算と回路
NOT演算(否定演算)
NOT演算とは、論理変数の真理値を反転する演算(否定演算)である。NOT演算子は通常、単項演算子として使用され、論理変数を1つだけ取る。
| $$A$$ | $$Y=\overline{A}$$ |
| 1(真) | 0(偽) |
| 0(偽) | 1(真) |
$$A=0 \rightarrow \bar{A}=1 \\A=1 \rightarrow \bar{A} =0$$と書ける。図1はBuffer とNOT回路の回路図記号である。実際の回路では、例えば、\(+5\;V\)を「1」に、\(0\;V\)を「0」に対応させることで、\(\{1,0\}\)の2値を実現している。
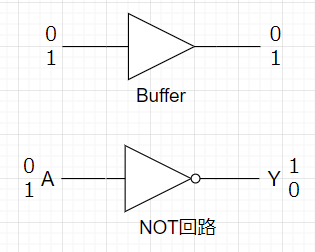
※以下、真を「1」、偽を「0」とする。(当然、逆に値{1,0}を定義しても良い。)
真理値表
真理値表とは、論理関数の、入力の全てのパターンとそれに対する結果の値を、表にしたものである。真理値表は、論理演算の入力値と出力値の対応関係を表として表したもので、一般的な形式では表の左側の列に入力を、右側の列に出力をそれぞれ並べる。各行に入力の組み合わせと、その時の出力を記入する。
OR演算(論理和)
OR演算とは、2つの論理変数の真理値のうち、いずれか一方が真「1」である場合に、真の値「1」を返す演算である。OR演算子は通常、二項演算子として使用され、論理変数を2つ取る。
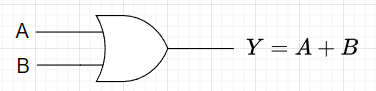
表2はOR演算の真理値表である。また、図2がOR回路の回路図記号である。
| $$A$$ | $$B$$ | $$Y = A + B$$ |
| 0 | 0 | $$0$$ |
| 0 | 1 | $$1$$ |
| 1 | 0 | $$1$$ |
| 1 | 1 | $$1$$ |
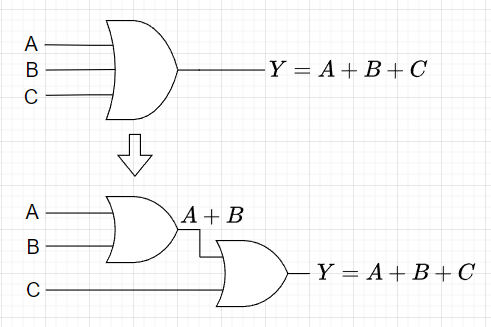
3変数以上のOR論理関数は、2変数のOR論理関数を組み合わせることで実現できる。つまり$$A+B+C = (A+B)+C$$とできる。図3は3変数OR回路が2変数OR回路の組み合わせで実現できることを示している。
AND演算(論理積)
AND演算とは、2つの論理変数の真理値がどちらも真「1」である場合にのみ、真の値「1」を返す演算である。AND演算子は通常、二項演算子として使用され、論理変数を2つ取る。
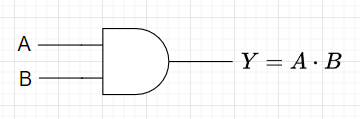
表3はAND演算の真理値表である。また、図4がAND回路の回路図記号である。
| $$A$$ | $$B$$ | $$Y=A \cdot B$$ |
| 0 | 0 | $$0$$ |
| 0 | 1 | $$0$$ |
| 1 | 0 | $$0$$ |
| 1 | 1 | $$1$$ |
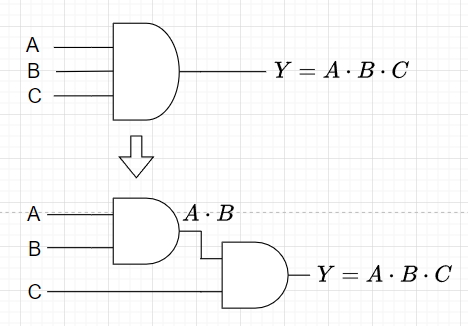
3変数以上のAND論理関数は、2変数のAND論理関数を組み合わせることで実現できる。つまり$$A \cdot B \cdot C = (A \cdot B) \cdot C$$とできる。図5は3変数AND回路が2変数AND回路の組み合わせで実現できることを示している。
論理関数の完全性
論理関数の完全性とは、任意の論理関数は、NOT,AND,ORの3つの演算子だけで構成できることを言う。
論理関数を\(f\)、論理変数を\((x_1,x_2,x_3, \cdots, x_n)\) とする。\(x_1,x_2, \cdots x_n\)は\(\{1\; , \;0\}\)の値をとる。論理関数値\(z\)は、$$z = f(x_1,x_2,x_3, \cdots , x_n)$$で表せ、論理関数値\(z\)は、\(\{1\; , \;0\}\)の値をとる。
\(n\)個の論理変数があるとき、組み合わせの数は\(2^n\)となる。\(2^n\)個の論理変数の組み合わせに対して、論理関数値の組み合わせは2通りの\(\{1,\;0\}\)となる。従って、可能な論理関数の数は、\(2^{2^n}\)個となる。
論理関数は、引数の全ての組み合わせに対して、関数値\(\{0\; , \;1\}\)を対応させた表によって表せる。例えば、引数を\(A,\;B\)の2個とすると、その組み合わせは、4通りとなり、それに対して関数値は\(2^4=16\)通りとなる。表4が2変数の論理関数の真理値表である。
| A | B | ① | ② | ③ | ④ | ⑤ | ⑥ | ⑦ | ⑧ | ⑨ | ⑩ | ⑪ | ⑫ | ⑬ | ⑭ | ⑮ | ⑯ |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
表4において関数値が②となるところが、AND関数であり、関数値が⑧となるところが、OR関数である。この表より、16通りの関数が構成できることが分かる。これら16通りの関数がNOT,AND,ORの3つの演算子で実現できることが示せれば、2変数論理関数の完全性がいえる。
NOR演算、NAND演算
NOR と NAND は、論理演算の 2 つの基本演算である。NOR 演算は、2 つの論理変数の真理値がどちらも偽「0」である場合にのみ、真の値「1」を返し、一方、NAND 演算は、2 つの論理変数の真理値がどちらも真「1」である場合にのみ、偽の値「0」を返す。また、NOR 演算は、OR 演算の否定として、NAND 演算は、AND演算の否定として、表現することができる。
NOR演算
NOR 演算は、2 つの論理変数の真理値がどちらも偽「0」である場合にのみ、真の値「1」を返す演算である。NOR 演算子は通常、三項演算子として使用され、論理変数を 2 つ取る。NOR 演算の真理値表を表5に示す。
| $$A$$ | $$B$$ | $$A + B$$ | $$Y= \overline{A+B} $$ |
| 0 | 0 | 0 | $$1$$ |
| 0 | 1 | 1 | $$0$$ |
| 1 | 0 | 1 | $$0$$ |
| 1 | 1 | 1 | $$0$$ |
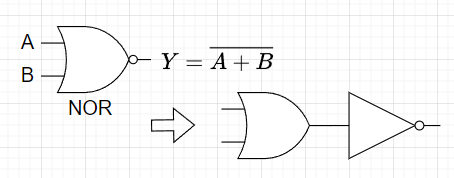
図6は、NOR回路の図記号とNOR回路がOR回路とNOT回路から構成されることを示している。
NAND演算
NAND 演算は、2 つの論理変数の真理値がどちらも真「1」である場合にのみ、偽の値「0」を返す演算である。NAND 演算子は通常、三項演算子として使用され、論理変数を 2 つ取る。NAND 演算の真理値表を表6に示す。
| $$A$$ | $$B$$ | $$A \cdot B$$ | $$Y= \overline{A \cdot B} $$ |
| 0 | 0 | 0 | $$1$$ |
| 0 | 1 | 0 | $$1$$ |
| 1 | 0 | 0 | $$1$$ |
| 1 | 1 | 1 | $$0$$ |
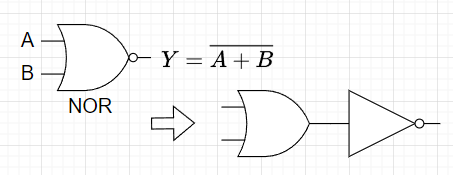
図7は、NAND回路の図記号とNAND回路がAND回路とNOT回路から構成されることを示している。
NAND演算、NOR演算の完全性
NAND と NOR は、論理演算の基本演算であり、任意の論理関数は、NAND または NOR だけで構成することができ、この性質をNAND と NOR の完全性と言う。
NAND と NOR の完全性は、論理回路やプログラミング言語の設計において、重要な意味を持っている。論理回路は、論理ゲートと呼ばれる素子によって構成されおり、NAND や NOR などの論理演算を行うことができる。NAND と NOR の完全性により、任意の論理関数をNAND または NOR の論理ゲートだけで実装することができる。
図8はNOR回路、NAND回路からNOT回路を構成する方法を示している。表7がその真理値表である。
| $$X$$ | $$A$$ | $$B$$ | $$Y=\overline{X}$$ |
| 0 | 0 | 0 | $$1$$ |
| 1 | 1 | 1 | $$0$$ |
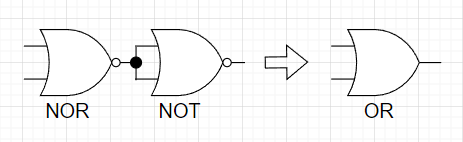
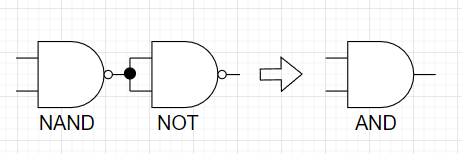
このNOT回路を使うことで、図9,図10に示すように、NOR回路からOR回路を、NAND回路からAND回路を構成することができる。
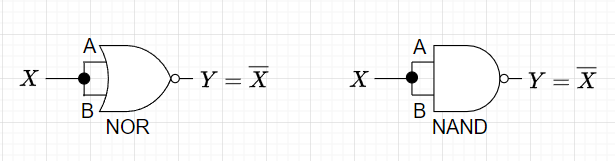
ド・モルガンの法則
ド・モルガンの法則とは、論理演算の 2 つの法則である。
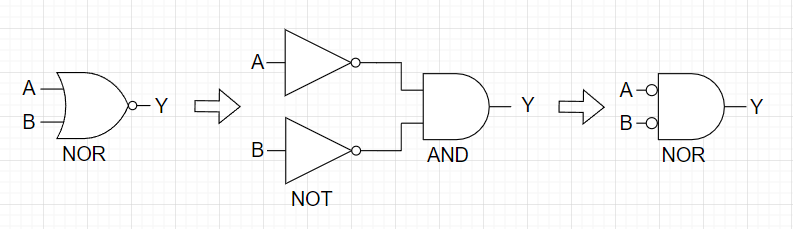
・ド・モルガンの第 1 法則:AとBの論理和の否定は、Aの否定とBの否定の論理積と等しい。$$\overline{A+B} = \overline{A} \cdot \overline{B}$$図11が回路図での表現、表8が真理値表である。
| $$A$$ | $$B$$ | $$\overline{A}$$ | $$\overline{B}$$ | $$Y=\overline{A+B}=\overline{A} \cdot \overline{B}$$ |
| 0 | 0 | 1 | 1 | $$1$$ |
| 0 | 1 | 1 | 0 | $$0$$ |
| 1 | 0 | 0 | 1 | $$0$$ |
| 1 | 1 | 0 | 0 | $$0$$ |
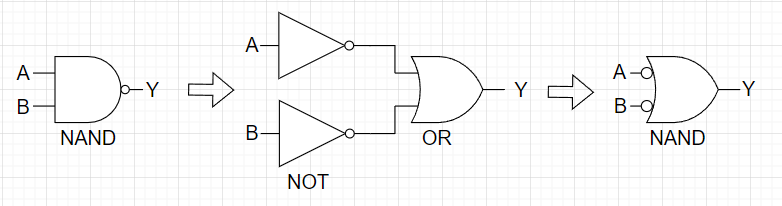
・ド・モルガンの第 2 法則:AとBの論理積の否定は、Aの否定とBの否定の論理和と等しい。$$\overline{A \cdot B} = \overline{A} + \overline{B}$$図12が回路図での表現、表9が真理値表である。
| $$A$$ | $$B$$ | $$\overline{A}$$ | $$\overline{B}$$ | $$Y=\overline{A \cdot B}=\overline{A} +\overline{B}$$ |
| 0 | 0 | 1 | 1 | $$1$$ |
| 0 | 1 | 1 | 0 | $$1$$ |
| 1 | 0 | 0 | 1 | $$1$$ |
| 1 | 1 | 0 | 0 | $$0$$ |


“2. 基本論理演算と回路” に対して1件のコメントがあります。
コメントは受け付けていません。