7. ダイオードによる基本論理回路
ダイオードは、半導体のpn接合によって一方向に電流を流す性質を持つ半導体素子である。この性質を利用して、論理回路を構成することができる。
ダイオードによる論理回路の基本的な動作は、
・ダイオードに順方向電圧を印加すると、ダイオードがオンになり、電流が流れる。
・ダイオードに逆方向電圧を印加すると、ダイオードがオフになり、電流が流れない。
である。この動作を利用して、AND、OR、NOTなどの論理ゲートを構成することができる。
接合ダイオードの特性
図1は、接合ダイオードの回路図記号である。\(A\)(アノード)側がp型半導体(多数キャリアが正孔)、\(K\)(カソード)側がn型半導体(多数キャリアが電子)である。\(A\)側の電位を高くし、\(K\)側の電位を低くした場合が順方向で、\(A \rightarrow K\)が電流の流れる方向である。
ダイオードの動作原理の詳細は、pn接合ダイオードを参照して欲しい。
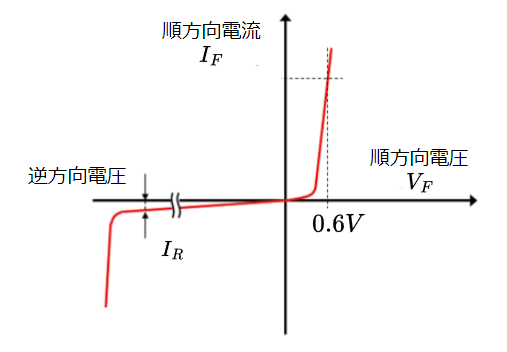
図2は、ダイオードの静特性である。順方向電圧が約0.6 V以上になると電流が大きく流れ出す。一方、逆方向電圧では、ほとんど電流が流れない。ただし、逆方向電圧が非常に高くなると逆方向電流が急激に流れ出す。これをブレーク・ダウン(降伏現象)という。
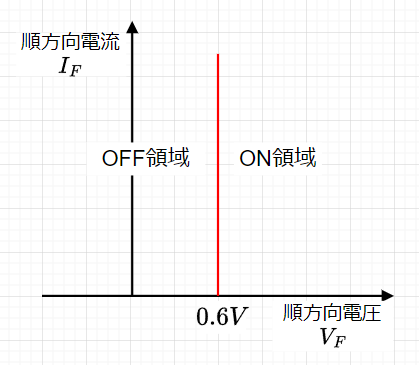
ダイオードによる論理回路では、図3に示すように、ダイオードの静特性をディジタル近似して、「ON領域」「OFF領域」のスイッチング動作で考える。
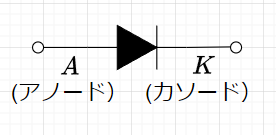
ダイオードによるAND回路
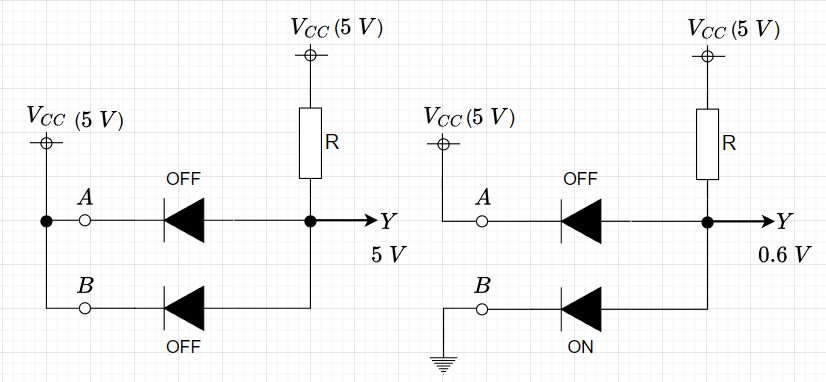
図4にダイオードによるAND回路の構成を示す。ダイオード2つのアノード(A)側を抵抗\(R\)を介して電源\(V_{CC}\)(\(5\; V\))に接続する。ここで、\(A,B\)を入力(論理変数)で\(Y\)を出力(論理結果)とする。入力の片方でも\(0\; V\)にすれば対応するダイオードがONになり、ダイオードの順方向電圧を\(0.6 \; V\)とすると、出力は\(0.6 \; V\)になる。\(A,B\)両方の入力に\(5 \; V\)がかかったときのみ、両方のダイオードがOFFとなり、電流が流れないため抵抗の電圧降下がなく、出力が\(5 \; V\)となる。表1にダイオードによるAND回路の動作表を示す。\(5 \; V\)をHレベル「1」とみなし、\(0.6 \; V\)をLレベル「0」とみなせば、AND動作となっていることがわかる。
| \(A\) | \(B\) | \(Y\) | |||
| \(0\;V\) | 0 | \(0\;V\) | 0 | \(0.6 \;V\) | 0 |
| \(0\;V\) | 0 | \(5 \; V\) | 1 | \(0.6 \;V\) | 0 |
| \(5 \; V\) | 1 | \(0\;V\) | 0 | \(0.6 \;V\) | 0 |
| \(5 \; V\) | 1 | \(5 \; V\) | 1 | \(5 \; V\) | 1 |
ダイオードによるOR回路
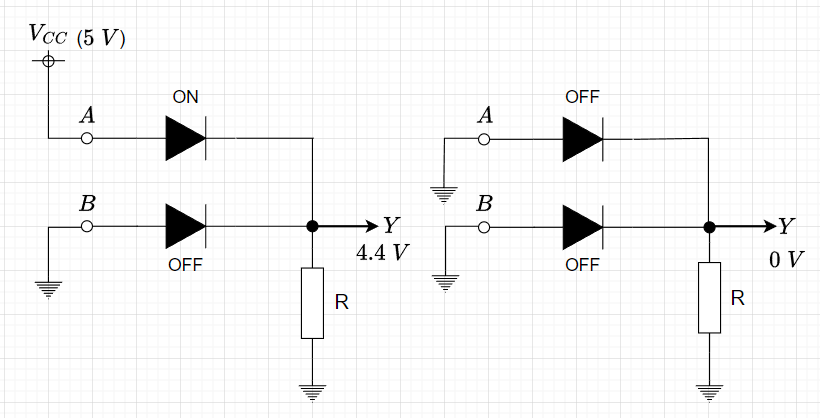
図5にダイオードによるOR回路の構成を示す。ダイオード2つのカソード(K)側を抵抗\(R\)を介してGND(\(0 \; V\))に接続する。ここで、\(A,B\)を入力(論理変数)で\(Y\)を出力(論理結果)とする。入力の片方でも\(5\; V\)にすれば対応するダイオードがONになり、ダイオードの順方向電圧を\(0.6 \; V\)とすると、電源電圧\(V_{CC}\)(\(5 \;V\))から\(0.6 \; V\)降下して、出力は\(4.4 \; V\)になる。また、\(A,B\)両方の入力を\(0 \; V\)にしたときのみ、出力が\(0 \; V\)となる。表2にダイオードによるOR回路の動作表を示す。\(4.4 \; V\)をHレベル「1」とみなし、\(0 \; V\)をLレベル「0」とみなせば、OR動作となっていることがわかる。
| \(A\) | \(B\) | \(Y\) | |||
| \(0\;V\) | 0 | \(0\;V\) | 0 | \(0\;V\) | 0 |
| \(0\;V\) | 0 | \(5 \; V\) | 1 | \(4.4 \; V\) | 1 |
| \(5 \; V\) | 1 | \(0\;V\) | 0 | \(4.4 \; V\) | 1 |
| \(5 \; V\) | 1 | \(5 \; V\) | 1 | \(4.4 \; V\) | 1 |
ダイオード論理回路の問題点
ダイオード論理回路は、出力に負荷(次の段の論理回路など)が接続されなければ、論理動作が成り立つが、負荷がある場合は、誤動作を生じる。図6はダイオードAND回路にダイオードOR回路を接続した場合の回路図である。図6の下図に論理回路記号で示したように、AND,OR接続で入力が図のような場合、出力は「H」となる。
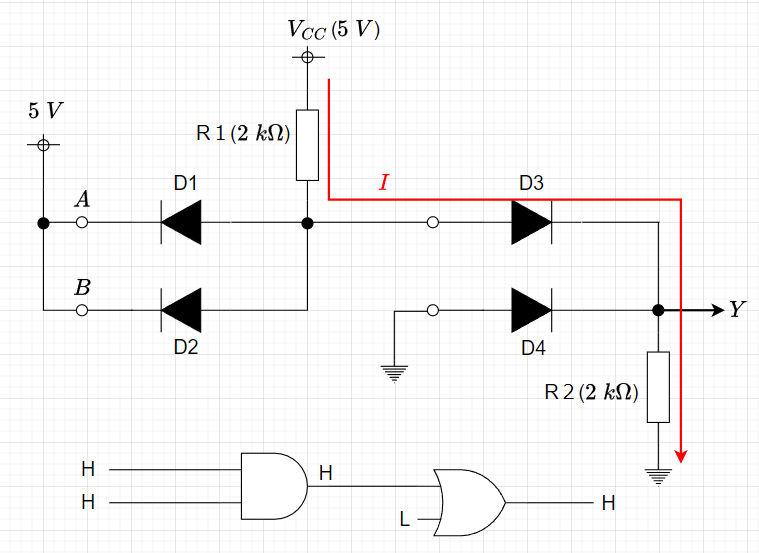
これをダイオード論理回路で実装すると、入力\(A,B\)が\(5 \; V\)の場合、D1,D2はOFFとなる。D3はONとなるため、電流\(I\)は、$$I = \frac{V_{CC} - V_F}{R1 + R2}$$となる。従って、出力\(Y\)の電圧\(V_Y\)は、$$V_Y = I \times R2 = \frac{5 - 0.6}{4000} \times 2000 = 2.2 \;V$$となる。この電圧値は、「H」とも「L」とも判定できない値であり、論理回路とは不適となる。
この問題点を解決する方式として、別項で説明するトランジスタを利用したDTL、TTLがある。


“7. ダイオードによる基本論理回路” に対して1件のコメントがあります。
コメントは受け付けていません。