11. CMOS論理ICの特性
CMOS(Complementary Metal-Oxide-Semiconductor)FETによる論理回路は、金属酸化膜半導体(MOS)FETのpMOS-FETとnMOS-FETを組み合わせた論理回路構成の方式で、ディジタル回路で広く使用される集積回路技術の一つである。CMOS論理回路の主な電気特性は、以下である。
・低消費電力(Low Power Consumption):CMOS論理回路は、静止状態での電力消費が非常に低い。これは、CMOS論理回路が静止状態でエネルギーをほとんど消費しないためである。
・高S/N比(High Signal-to-Noise Ratio: SNR):pMOS-FETとnMOS-FETが互いに補完的な動作をするため、CMOS回路は高い信号対雑音比(SNR)を実現する。
・高集積度(High Integration Density):CMOSは非常に高い集積度を持つことが可能である。FETの構造は、比較的単純であり、小型化が容易なため、多くのFETを半導体チップに配置できる。
・低電圧動作(Low Voltage Operation):CMOS論理回路は一般に低い動作電圧で動作できる。
・高ノイズ耐性(High Noise Immunity):CMOS論理回路は入力信号がL(0)またはH(1)であることを識別しやすく、外部からのノイズに対する耐性が高い。これにより、ディジタル信号の正確な処理が可能である。
IC内部の各CMOS論理回路の電気的特性はプロセスにより異なるため、特性の解析にはCADツールなどが必要である。
以下に説明する電気的特性は、CMOSの汎用ロジックIC(74シリーズ)などを外部から見た時の電気的特性である。特性では、静特性と動特性を考えるが、静特性は、入出力特性、駆動能力など、時間が関係しない特性を示しており、動特性は、伝搬遅延時間など、時間に関係した特性である。
ここでは、74VHC04FTの規格表を基に、電気的特性をまとめる。
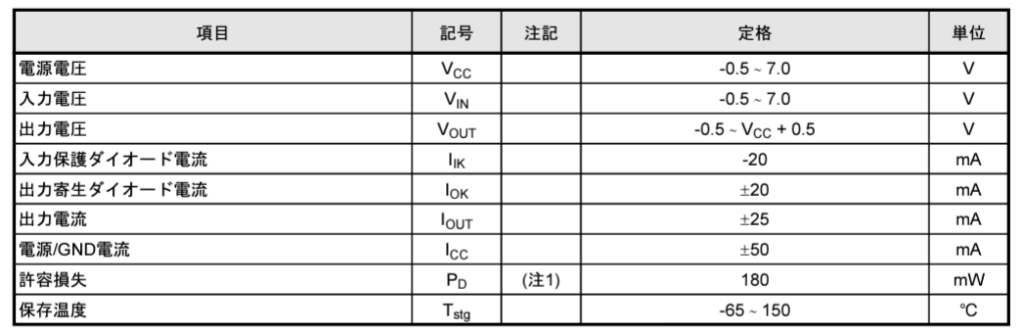
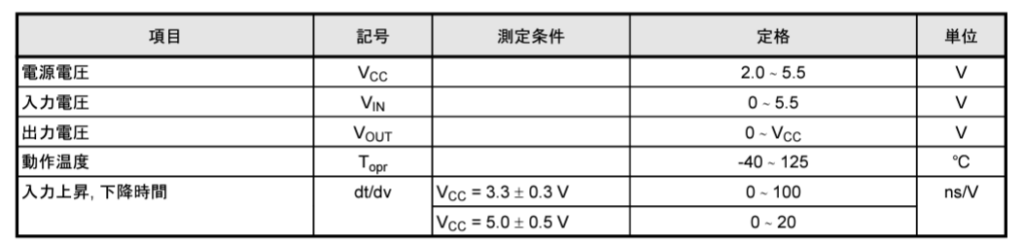
図1は74VHC04FTの絶対最大定格である。絶対最大定格は、一瞬たりとも超えてはならない値であり、1つの項目も超えてはならない値である。
CMOSの静特性
入出力特性
ディジタル回路の出力は、入力が一定値に達するまでは、一定のHレベルかLレベルを保つ。入力が一定値に達したときに出力のHレベル、Lレベルが切り替わる。この出力が切り替わるときの入力電圧をスレッショルドレベル(\(V_{th}\))という。
図1はCMOSで構成したNOT回路の入出力特性である。出力電圧\(V_{out}\)のHレベルは電源電圧\(V_{CC}\)に近く、LレベルはGND(\(0\;V\))に近くなる。また、\(V_{th}\)は、おおよそ電源電圧\(V_{CC}\)の半分程度となる。 CMOS は、スレッショルドレベル付近の電圧変化が非常に急峻で、 Lレベル、Hレベルともに理想的なディジタル回路の特性を持っている。
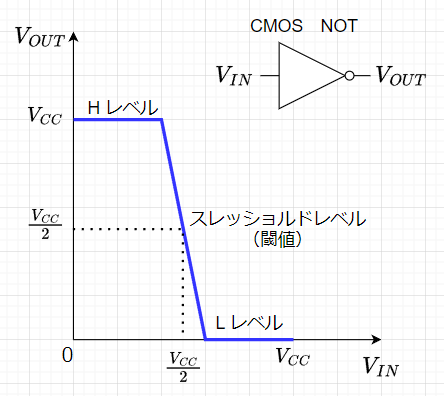
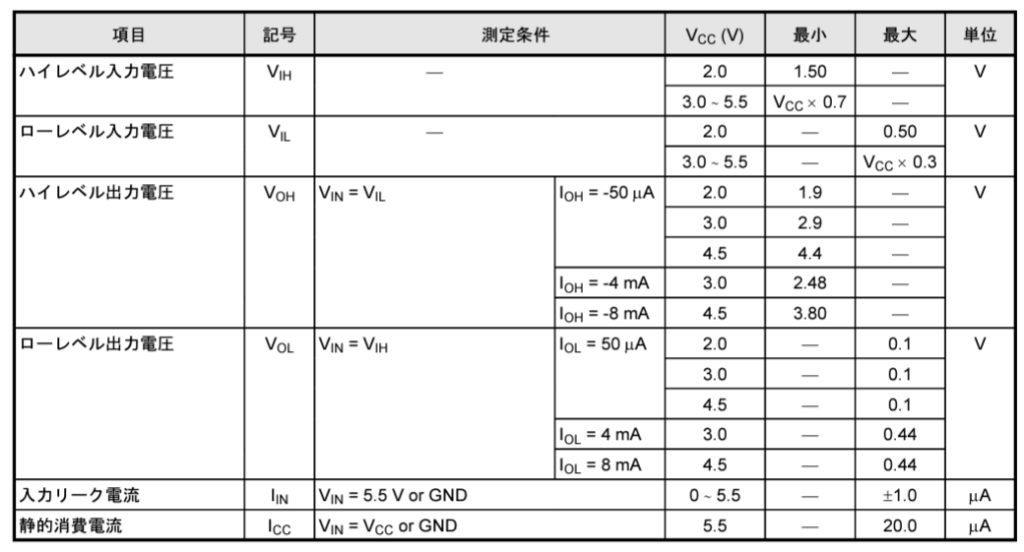
図3に74VHC04FTのDC特性(\(T_a=-40 \sim 85 \;℃\):周囲温度-40~85℃の雰囲気中)を示す。
ノイズマージン
CMOSのIC同士を接続する場合、図3の規格表を基に、まず、出力側の電圧、\(V_{OL}\) と\(V_{OH}\) を決める。電源電圧\(V_{CC}\)を\(4.5 \; V\)として、CMOSのIC同士を接続する場合で考えると、出力電流が小さいと見て、Hレベル出力電圧\(V_{OH}\)は、最小値で\(4.4 \;V\)、また、Lレベル出力電圧\(V_{OL}\)は、最大値で\(0.1\;V\)と読み取れる。
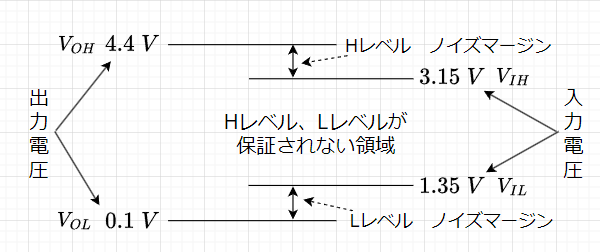
次に、入力側の電圧\(V_{IL}\) と\(V_{IH}\) を決める。\(V_{IH}\) は、これより高ければ H レベルとして認識してくれる値で、最小値を考えて \(3.15 \; V\) を読み取る。\(V_{IL}\) はこれより低ければ L レベルとして認識してくれる値で、最大値の\(1.35 \;V\) を読み取る。結果として Hレベルでは\(V_{OH}\) と\(V_{IH}\) 分、 L レベルでは \(V_{OL}\)と\(V_{IL}\)分の余裕を持って Hレベルと Lレベルの受け渡しができることがわかる。これをノイズマージン(雑音余裕度)と呼ぶ。ここでは H レベル、 L レベル共に \(1.25\; V\) のノイズマージンがあることになる。ノイズマージンが小さいと、小さいノイズでも誤動作する可能性がある。ここでは、すべての値に規格表の最悪値を用いたが、このような設計の仕方をワーストケースデザインと呼ぶ。どのような環境でも動作させるためには、ワーストケースデザインが必要である。
駆動能力
CMOSの駆動能力は、その出力バッファの能力を指す。具体的には、CMOSデバイスが他のデバイスやロードに対してどれだけの電流を供給(ソース電流)できるか、または吸収(シンク電流)できるかを示す。CMOSの駆動能力は、その出力電流の大きさによって決まる。例えば、74VHC04FTというCMOSデバイスでは、図3のDC特性から分かるように、出力電流\(I_{OH}\)と\(I_{OL}\)(HレベルとLレベルでの出力電流)はほぼ同等の駆動能力である。駆動能力は、CMOSデバイスが他のデバイスと接続する際に重要となる。また、具体的な駆動能力は、使用するCMOSデバイスやその設計、適用されるシステムなどによる。
74VHC04FTの場合、図3より、電源電圧\(V_{CC}=4.5\;V\)の設定で、出力電流を\(I_{OH}=-50 \; \mu A\)とすると、ハイレベルの出力電圧\(V_{OH}\)は、最小で\(4.4 \; V\)であるが、\(I_{OH}=-8 \;mA\)にすると、\(V_{OH}\)は、\(3.8 \;V\)に低下する。また、ローレベルの出力電圧\(V_{OL}\)は、最大で\(0.1 \; V\)(@ \(I_{OL}=-50 \; \mu A\))から\(0.44 \;V\)(@ \(I_{OL}=8 \; mA\))に上昇する。このように駆動電流(シンク電流、ソース電流)により、Hレベル、Lレベルの出力電圧が変化することは、耐雑音性などに影響するので注意が必要である。
素子の電気的な駆動能力を表す特性の指標として、一つの素子の出力に複数の素子を繋ぐことを考える。図4(Lレベルファンアウト)に示すように、 L レベル出力の場合、それぞれの素子から電流が流れ込んでくる。この状態をシンクロードと呼ぶ。繋がった素子が多くなり、この流れ込んでくる電流 \(I_{OL}= n \times I_{IL}\) が大きくなると、 ON になっている FET の抵抗によりLレベルの出力電圧が上昇してしまう可能性がある。 \(V_{OL}\) が上昇するとノイズマージンが維持できなくなる。一方、図4(Hレベルファンアウト)に示すように、Hレベル出力の場合、電流は流しだす方向になり、これをソースロードと呼ぶ。流しだす電流\(I_{OH}=n \times I_{IH}\) が大きすぎると H レベルの出力電圧が低下する可能性がある。図5にCMOS NOT回路のシンクロード、ソースロードの動作を示す。
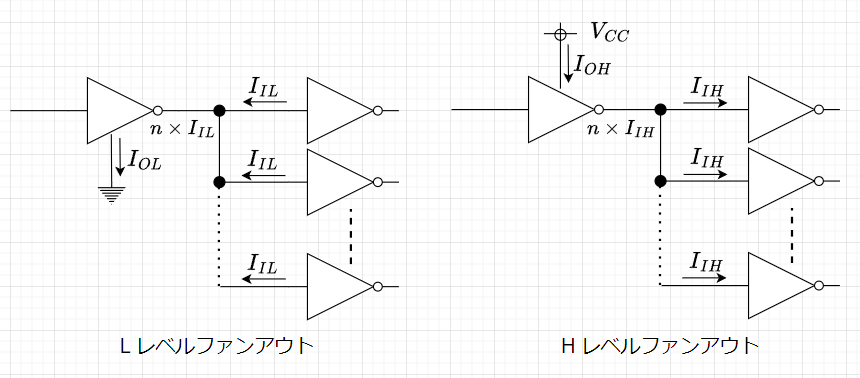
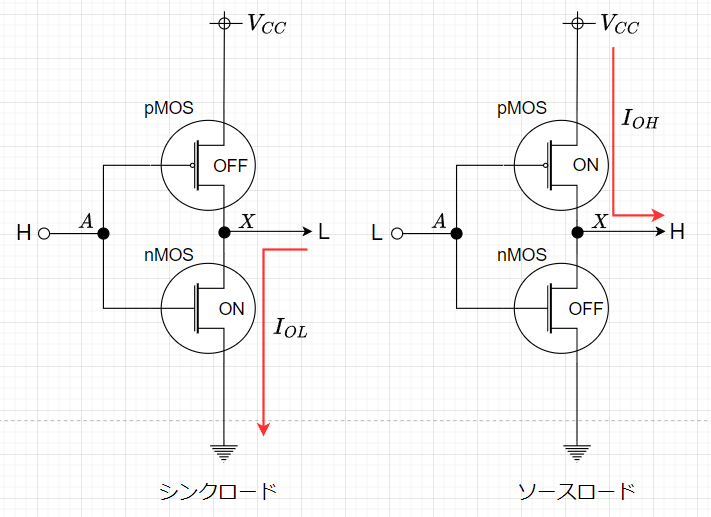
CMOS は電圧駆動型電流素子でなので、ゲートはソース、ドレインとは絶縁されており、繋がった各素子への入力電流 \(I_{IN}\)は小さい。規格表 の\(I_{OL}\)と \(I_{OH}\)を使って、 \(\frac{I_{OL}}{I_{IN}} , \; \frac{I_{OH}}{I_{IN}}\)の最大値を計算すると素子一つの出力に何個の入力が接続できるか計算できる。この値をファンアウトと呼ぶ。
図3からファンアウトを計算すると、出力電圧の低下、上昇が小さい条件では、$$\frac{50\; \mu A}{1 \; \mu A}=50$$また、出力電圧の低下、上昇が大きい条件とした場合は、$$\frac{8\; mA}{1 \; \mu A}=8000$$となる。しかし、実際には素子自体の入力容量、配線の容量性負荷、誘導性負荷の問題があるため、ファンアウトは十数個程度が妥当である。このようにCMOSのICの場合は、IC自体の出力電流などの電気的特性以外でファンアウトが決まると考えて良い。
CMOSの動特性
伝搬遅延時間
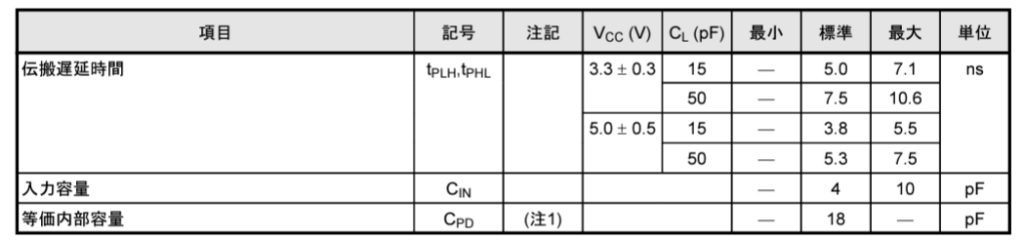
図7は、AC特性の表で動特性を表している。ディジタル回路の動特性は、主に伝搬遅延時間で表される。出力電圧のLレベルを\( V_{OL}\) 、 Hレベルを\(V_{OH}\) とする。立ち下り伝搬遅延時間\(t_{PHL}\) は入力がHレベルとLレベルの差の50% を越えてから、これに反応して出力が \(V_{OH}\) から\(V_{OL}\)の差の50%を切るまでの時間とする。
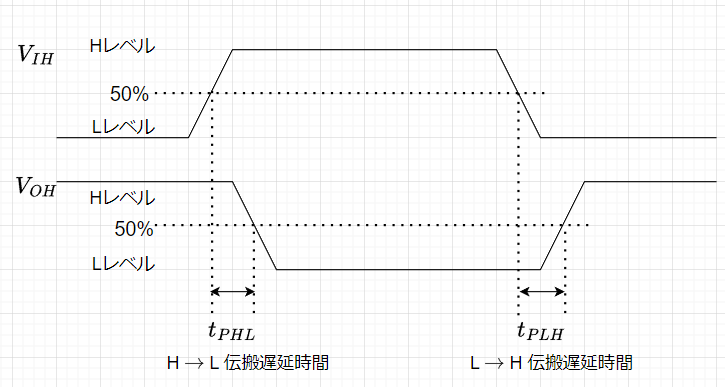
CMOS の場合、おおよそ\(V_{OH}=V_{CC} , \;\; V_{OL}=GND\) と見なして良いので入力が \(\frac{V_{CC}}{2}\) を越えてから、出力が \(V_{CC}\) から \(\frac{V_{CC}}{2}\) を切るまでの時間と考えて良い。立ち上がり伝搬遅延時間\(t_{PLH}\) は、入力が \(\frac{V_{CC}}{2}\) を切ってから、出力が\(0 \;V\) から \(\frac{V_{CC}}{2}\) を越えるまでの時間である。 \(\frac{V_{CC}}{2}\) をスレッショルドレベルと考えて良いので、この値は入力がスレッショルドレベルをよぎってから、出力がスレッショルドレベルをよぎるまで、つまり、ディジタル的な信号の伝わる時間を示す。\(t_{PHL}\) と\(t_{PLH}\) は同じと見なせる場合もあるが、素子によっては異なる場合もある。
消費電力
CMOSは入力が変化しない場合、pMOSかnMOSのどちらかは必ずOFFになるので、回路のどこかは電気的に切り離されている。従って、静止状態でのCMOSの消費電力は、漏れ電流(\(I_{CC}\))による電力消費のみである。漏れ電流\(I_{CC}\)は、通常の使用温度領域(\(Ta=25\;℃\))では非常に小さな値(\(2 \mu A\))となる。
しかし、入力が変化し、出力が切り替わるとレベルが変化するため、ONになるFETから負荷の容量に充電電流が流れる。図7の「AC特性」において\(C_{PD}\)は、動作消費電流から算出したIC内部の等価容量である。また、無負荷時のゲート当たりの平均消費電流は、$$I_{CC(opr)} = C_{PD} \times f_{IN} \times V_{CC} + I_{CC}/6$$ である。ここで、\(V_{CC}\)は電源電圧、\(f_{IN}\)は動作周波数である。
漏れ電流\(I_{CC}\)は非常に小さい値なので、通常は、消費電力に考慮しなくてよい。従って、CMOS消費電力は、$$P = (C_L + C_{PD}) \cdot f_{IN} \cdot V_{CC}^2$$と表せる。\(C_L\)は負荷容量である。すなわち、CMOSの消費電力は、動作周波数と容量に比例し、電源電圧の2乗に比例する。従って、電源電圧を下げることは、消費電力の低減に非常に有効であり、プロセスの改善による、低電圧化は重要な技術である。

