13. 半加算器、全加算器

半加算器（Half Adder）と全加算器（Full Adder）は、ディジタル回路で使用される基本的な論理回路であり、二進数の加算を実行するために使われる。これらの回路は、コンピュータやディジタル機器などで算術演算を実現する基本要素である。

半加算器

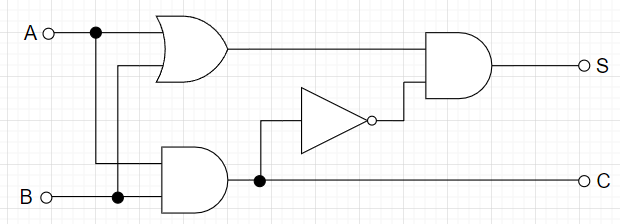
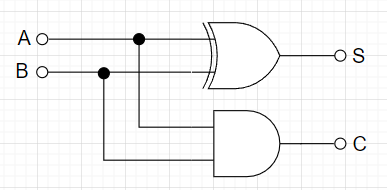
半加算器は、２つの１ビットの入力（AとB）を受け取り、2つの出力、和（S）と繰り上がり（C）を生成する回路である。表１に半加算器の真理値表を示す。$$S = \overline{A}\cdot B + A \cdot \overline B \\ C = A \cdot B$$となるので、回路は図１のようになる。さらに、和（S）は\(A\)と\(B\)の排他的論理和（EXOR）、繰り上がり\(C\)は、\(A\)と\(B\)の論理積となっているので、図２のように回路図をまとめることができる。

\(A\)	\(B\)	\(S\)	\(C\)
0	0	0	0
0	1	1	0
1	0	1	0
1	1	0	1

全加算器

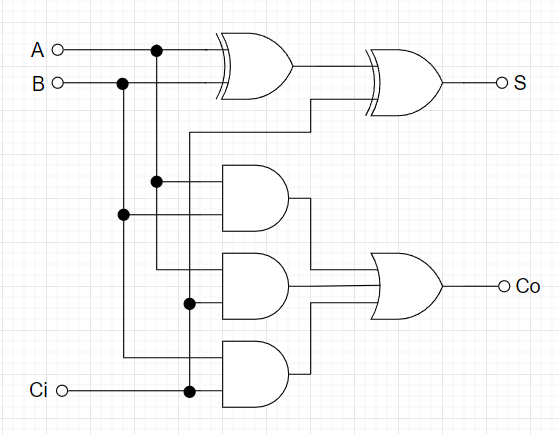
全加算器は、３つの１ビットの入力（A、B、前の段からの繰り上がりCin）を受け取り、２つの出力、和（S）と新たな繰り上がり（Co）を生成する回路である。全加算器は、半加算器と同様な和を生成するとともに、前の段からの繰り上がりを考慮して新たな繰り上がりを生成する。これにより、複数桁の二進数の加算を行うことができる。表２に全加算器の真理値表を示す。
和 （S）は、 3つの入力ビットA、B、Cin（前の段の繰り上がり）のXORを取る。$$S = A \oplus B \oplus C_{in}$$ 新たな繰り上がり （Co）は、 ３つの入力ビットA、B、Cinのうち、少なくとも２つが１であれば、またはすべてが１であれば新たな繰り上がりが発生する。$$C_o = (A \cdot B) + (A \cdot C_{in}) + (B \cdot C_{in})$$図３に全加算器の回路図を示す。

\(A\)	\(B\)	\(C_{in}\)	\(S\)	\(C_o\)
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1