1. ディジタル信号
信号はその性質や時間的な変化に基づいてさまざまな方法で分類できる。ここでは、ディジタル信号処理に関連した信号の分類を示す。
1)アナログ信号とディジタル信号
・アナログ信号: 連続的な時間と連続的な振幅を持つ信号。例えば、アナログ音声信号は連続した波形として表現される。
・ディジタル信号::離散的な時間と離散的な振幅を持つ信号。デジタル信号は通常、数値で表現され、離散的なサンプルを含む。例えば、ディジタル音声信号、画像信号が該当する。
2)連続信号と離散信号
・連続信号:信号の値が連続的な範囲で変動する。アナログ信号は連続信号の一例である。
・離散信号: 信号の値が離散的な値のみを取る。ディジタル信号は離散信号の一例である。
3)周期信号と非周期信号:
・周期信号: 一定の周期で繰り返される信号。正弦波や三角波等が周期信号である。
・非周期信号:特定の周期性を持たない信号。ランダムなノイズ信号等が非周期信号である。
アナログ信号とディジタル信号
時間的に連続した変化、例えば、気温などを適当なセンサで電気信号に変換した信号を連続時間信号といい、これに対して、気温を1時間毎に記録したような時間的に不連続な信号を離散時間信号という。時刻を表す変数\(t\)を用いてある信号を関数\(x(t)\)で表せば、\(x(t)\)は任意の時刻における信号の振幅を意味している。時刻が連続か不連続かによって、連続時間信号と離散時間信号に分けられ、連続時間信号は、振幅が連続した値をとるアナログ信号と離散的な値をとる多値信号に分けられる。離散時間信号は、連続的な振幅値をとるサンプル値信号と離散的な振幅値をとるディジタル信号に分けられる。図1(a)はアナログ信号を、図1(b)はディジタル信号を図的に表現したものである。
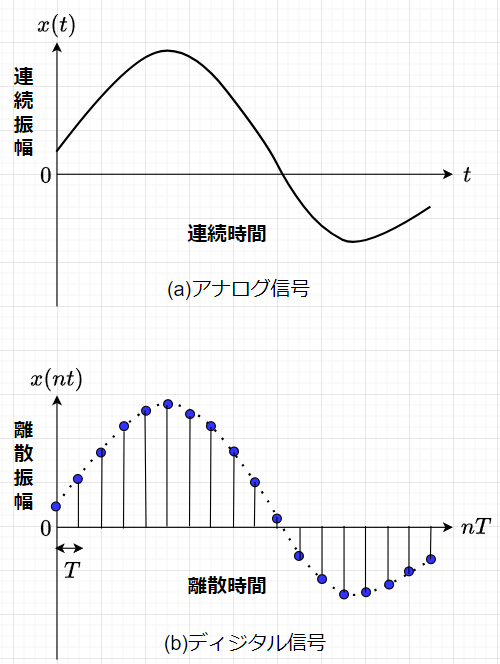
なお、ディジタル信号は離散値(量子化された値)しかとらない。このため量子化により生ずる誤差(量子化誤差)の影響を考慮しないといけないが、これを厳密に解析するのは煩雑で難しい。従って、ここでのディジタル信号は、時間的に離散化されているが、振幅値の離散化レベルは十分に細かい、すなわちサンプル値信号に近い信号であるものとして扱う。下記の量子化を参考にして欲しい。
ディジタル信号処理の概要
信号処理は、ある信号に必要な修正・加工を行うことをいう。図2(a)に示すようにアナログ信号をアナログ電子回路で直接処理するシステムをアナログ信号処理システムといい、受動素子の\(R,\;L,\;C\)を使ったフィルタ回路や能動素子のオペアンプを使ったフィルタ回路などが典型的なアナログ信号処理システムである。
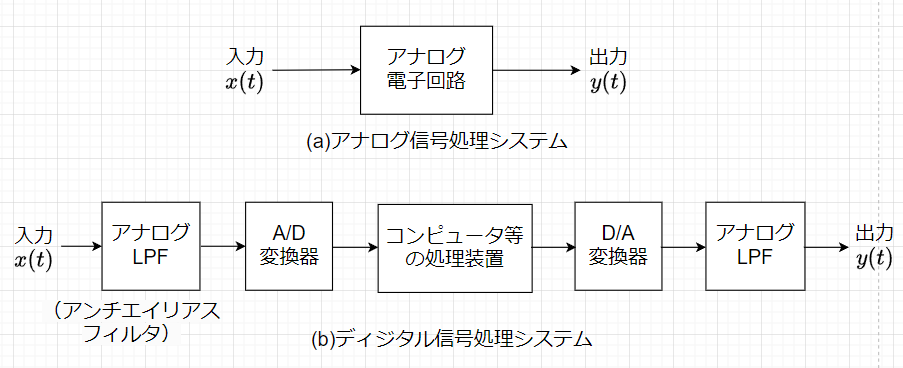
これに対して、図2(b)のように入力信号\(x(t)\)をA/D変換器により一旦ディジタル信号に変換して、コンピュータ等のディジタル回路により代数的演算で処理し、その後、D/A変換器によってアナログ信号に再変換して出力信号\(y(t)\)を得るシステムをディジタル信号処理システムという。
ディジタル信号処理を実現するには、先ず、アナログ信号をディジタル信号に変換する過程、すなわちA/D変換をしなければならない。A/D変換は、以下の3つの過程を経て行われる。
・標本化:アナログ信号を離散時間信号に変換する操作を標本化(サンプリング)という。アナログ信号\(x(t)\)を一定間隔\(T\)(サンプリング周期)で標本化するとサンプル値信号\(x(n)=x(nT)\)(\(n\):整数)が得られる。また、\(f_s = \frac{1}{T}\)をサンプリング周期という。
・量子化:サンプル値信号\(x(n)\)をあらかじめ決められたレベルに対応させる操作を量子化という。量子化レベルは離散値であり、サンプル値は連続値なので、その間には誤差が生じる。この誤差を量子化誤差(量子化雑音)という。量子化誤差は、デジタル信号の量子化レベルの数に依存するので、量子化レベルの数が多いほど、量子化誤差は小さくなる。しかし、量子化レベルの数が多いほど、ディジタル信号を表すために必要なビット数が増える。量子化誤差の影響は、アプリケーションによって異なる。例えば、音声信号をディジタル化する場合、量子化誤差が音質の低下につながる可能性がある。近年では、IC技術の高度化によりディジタル信号処理の多くの実装において十分なビット数が扱えるので、量子化誤差の影響を考慮する必要性は少なくなっている。
・符号化:量子化された振幅値を2進数のディジタルコードに変換することを符号化という。
以上のアナログ信号の標本化、量子化、符号化の一連の操作は、A/D変換器で実行する。
標本化によって元のアナログ信号の情報が失われないためには、標本化定理を満たす必要がある。
標本化定理(サンプリング定理)
標本化定理は、連続的な信号を離散的な信号に変換する際に、元の信号を完全に復元するために必要な最低限のサンプリング周波数を示した定理である。
標本化定理から必要なサンプリング周波数は、以下の式となる。$$f_s > 2f_h$$ここで、\(f_s\):サンプリング周波数[Hz]、\(f_h\):サンプリングされる元の信号の最高周波数[Hz]である。 (\(f_s =2f_h\)では、標本化定理は成立しないことに注意)
*サンプリング周波数は元の信号の2倍より高い周波数が必要。
(2倍以上ではないことに注意!)
2進数ディジタルコード
2進数の基本的なディジタルコードの表現には、ストレートバイナリと2の補数がある。
アナログ信号が単極性(ユニポーラ)の場合には、ストレートバイナリ、両極性(バイポーラ)の場合には、2の補数が多く使われる。
ストレートバイナリ
アナログ値をフルスケール\(10 \;V\)(\(0 \sim 10 \;V\))の電圧と仮定して、4bitのストレートバイナリコードに変換した場合を表1に示す。この例の場合、1ステップの電圧値はフルスケールの\(1/16\)なので、\(0.625 \;V\)となる。従って、\(1111\)のときのアナログ値は\(9.375 \;V\)となる。つまり、\(1111\)は\(9.375 \sim 10.000\;V\)を表していることになる。
| 10進 | ストレートバイナリ | \(10\;V\) フルスケール |
| 15 | 1111 | 9.375 V |
| 14 | 1110 | 8.750 V |
| 13 | 1101 | 8.125 V |
| \(\vdots\) | \(\vdots\) | \(\vdots\) |
| 2 | 0010 | 1.250 V |
| 1 | 0001 | 0.625 V |
| 0 | 0000 | 0.000 V |
2の補数表現
アナログ値をフルスケール\(\pm 5 \;V\)(\(-5 \sim +5 \;V\))の電圧と仮定して、4bitの2の補数に変換した場合を表2に示す。この場合でもストレートバイナリの例と同様に、1ステップの電圧値はフルスケールの\(1/16\)なので、\(0.625 \;V\)である。2進数の\(0111\)が10進数の\(+7\)を、2進数の\(1000\)が10進数の\(-8\)を表している。
| 10進 | 2の補数 | \(\pm 5\; V\) |
| \(+7\) | 0111 | + 4.375 V |
| \(+6\) | 0110 | +3.750 V |
| \(+5\) | 0101 | +3.125 V |
| \(\vdots\) | \(\vdots\) | \(\vdots\) |
| \(+1\) | 0001 | +0.625 V |
| \(0\) | 0000 | 0.000 V |
| \(-1\) | 1111 | -0.625 V |
| \(\vdots\) | \(\vdots\) | \(\vdots\) |
| \(-5\) | 1011 | -3.125 V |
| \(-6\) | 1010 | -3.750 V |
| \(-7\) | 1001 | -4.375 V |
| \(-8\) | 1000 | -5.000 V |
2の補数表現
2の補数とは、2進数の符号付き整数を表現する方法である。2の補数表現は、コンピュータで効率的に演算処理を行うために多く用いられる。
2の補数は、以下の手順で求めることができる。
1) 数値の絶対値を2進数に変換する。
2) 各ビットを反転させる。
3) 1を加算する。
【例】10進数の5を2の補数(4 bit)に変換
1) \(10 \rightarrow 0101\)
2) \(0101 \rightarrow 1010\)
3) \(1010 +1 \rightarrow 1011\)
よって、10進数5の2の補数は、1011となる。これが10進数の-5に相当する。
10進数の演算:\(5 +(-5) = 0\)
2進数の演算:\(0101 + 1011 =10000\)となる。4 bitの範囲で考えると0000である。つまり、\(1011\)は負の値を意味している。

