10. 離散時間システムの周波数特性

※離散時間システムの周波数応答（ディジタル制御）も参考にどうぞ。

LTIシステムのインパルス応答を\(h(n)\)として、そのシステムに複素正弦波数列の入力\(x(n) = e^{j n \omega T}\)を印可した時の出力\(y(n)\)は、$$y(n) = h(n) \ast e^{j n \omega T} = \sum_{k=0}^{\infty} h(k) e^{j (n - k) \omega T} \\= \left[ \sum_{k=0}^{\infty} h(k) e^{- j k \omega T} \right] e^{j n \omega T} \cdots \cdots(1)$$の畳み込み和で表せる。一方、インパルス応答\(h(n)\)の\(Z\)変換がシステムの伝達関数になるので、$$H(z) = \sum_{n=0}^{\infty} h(n) z^{-n} \cdot\cdots(2)$$となる。式(2)で\(z = e^{j \omega T}\)とおけば、式(1)の［　］内と等しくなる。従って、$$H(e^{j \omega T} )= \sum_{n=0}^{\infty} h(n) e^{-j n \omega T} \cdots \cdots (3)$$を定義し、これを離散時間システムの周波数伝達関数という。\(H(e^{j \omega T})\)は周期\(T\)（角周波数\(\omega_s = 2 \pi /T\)）の周期関数となる。\(|e^{j \omega T}|=1\)より、\(h(n)\)のフーリエ変換と\(z\)平面における単位円上で計算された\(h(n)\)の\(Z\)変換は等しいので、$$H(e^{j \omega T}) = \left. H(z) \right|_{z=e^{j \omega T}}$$が成り立つ。ただし、\(H(z)\)の収束領域内に単位円を含んでいなければならない。
ここで、\(\omega T = \Omega\)とおくと、式(3)は、$$H(e^{j \Omega}) = \sum_{n=0}^{\infty} h(n) e^{- j n \Omega}\;\cdots \cdots (4)$$となる。角周波数\(\omega\)の単位は[rad/s]、\(\Omega\)の単位は[rad]となる。\(H(e^{j \Omega})\)は周期\(2 \pi\)の\(\Omega\)の関数となるので、$$H(\Omega) = H(e^{j \Omega}) = \left. H(z)\right|_{z= e^{j \Omega}}$$と表せる。また、$$\Omega = \omega T = \frac{2 \pi f}{f_s} = 2 \pi f_N$$と書ける。（\(T\)：サンプリング周期、\(f_s\)：サンプリング周波数）\(f_N\)を正規化周波数という。\(f = f_s /2 \)で、\(\Omega = \pi\)であり、\(f_N = 0.5\)である。標本化定理より、離散時間システムの周波数特性は、\(f_s/2, \;\; f_N=0.5,\;\; \Omega=\pi\)で折り返すので、\(H(\Omega\)（正規化周波数）で周波数特性を描くことも多い。なお、\(\Omega\)をラジアン周波数と呼ぶ。

周波数特性

$$H(\Omega) = \sum_{n=0}^{\infty} h(n) e^{-j n \Omega}$$で表せる離散時間システムの周波数伝達関数は、一般に複素数なので、以下のように表せる。$$H(\Omega) = Re\{H(\Omega)\} + Im\{H(\Omega)\}\\ =|H(\Omega)|e^{j \angle H(\Omega)} \\ |H(\Omega)| = \sqrt{Re^2\{H(\Omega)\} + Im^2\{H(\Omega)\}} \\ \angle {H (\Omega)} = arg\{H(\Omega)\} = \tan^{-1} \frac{Im\{H(\Omega)\}}{Re\{H(\Omega)\}}$$ \(|H(\Omega)|\)を振幅特性（利得特性）、\(\angle{H(\Omega)}\)を位相特性という。この両方で、周波数特性という。

【例】インパルス応答が因果性の指数数列\(h(n) = b^n u(n) ,\;\;n \ge 0\)であるシステムの周波数特性を求める。

$$H(z) = \mathcal{Z}\{h(n)\} = \frac{1}{1 - bz^{-1}}, \;\;|z| > |b|$$なので、\(|b|<1\)であれば、収束領域内に単位円を含み、\(h(n)\)のフーリエ変換が存在するので、$$H(\Omega) = \left. H(z)\right|_{z= e^{j \Omega} }= \frac{1}{1- b e^{-j \Omega}}$$となる。この式は、オイラーの定理により、$$H(\Omega) = \frac{1}{1 - b \cos \Omega + j b \sin \Omega}$$となるので、振幅特性、位相特性は、$$|H(\Omega)| = \frac{1}{\sqrt{(1 - b \cos \Omega)^2 + (b \sin \Omega)^2}} \;\cdots \cdots(5) \\ \angle H(\Omega) =- \tan^{-1} \frac{b \sin \Omega}{1 - b \cos \Omega}\; \cdots \cdots (6)$$である。

Scilabによる周波数特性の計算

Scilabにより周波数特性を計算する。\(b=0.5\)として、\(\Omega = 0 \sim 2\pi\)（\(f= 0 \sim f_s\)）の範囲で振幅特性、位相特性を描く。スクリプトの青字部分は、式(5),(6)を計算しグラフにするスクリプト、緑字部分は、振幅特性をdBにし、横軸を対数にしたグラフにするスクリプト、赤字部分は、Scilabのbode関数を使ったスクリプトである。

【Scilab スクリプト】
//周波数特性
//Hz=1/(1-b*z^-1)=z/(z-b)
clear; clf();
pi=%pi; z=%z;
b=0.5;
w=0:0.01:2*pi;
H = 1./(sqrt((1- b.*cos(w)).^2 + (b.*sin(w)).^2)); pH = -atan((b.*sin(w))./(1 - b.*cos(w)));
scf(0);plot(w,H);
scf(1);plot(w,pH);
Hdb = 20*log10(H);
pHd = pH*180/pi;
scf(2);plot2d('ln',w,Hdb);
scf(3);plot2d('ln',w,pHd);
T=1;
Hz = z/(z-b);
Hzz=syslin(T,Hz);
scf(4);bode(Hzz,0.01,10,'rad');

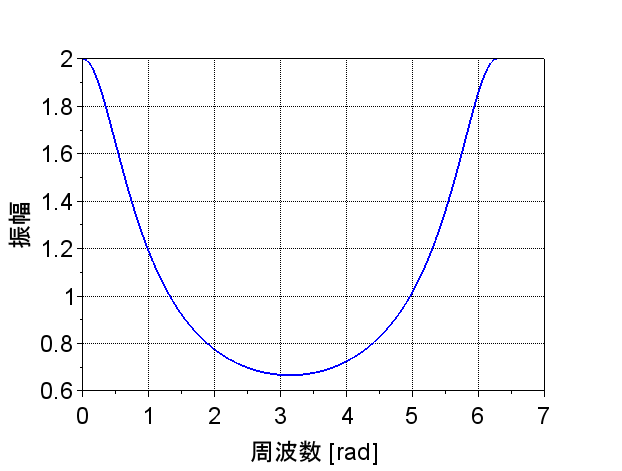
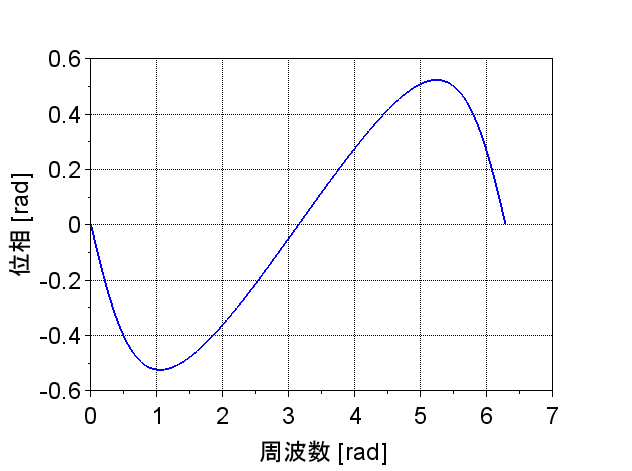
図１は、青字のスクリプトによる結果である。横軸は\(\Omega \;[rad]\)で、リニアスケールで表示している。位相は「rad」表示である。
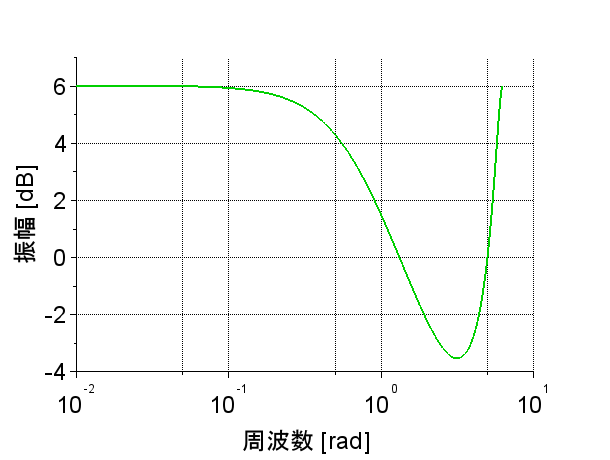
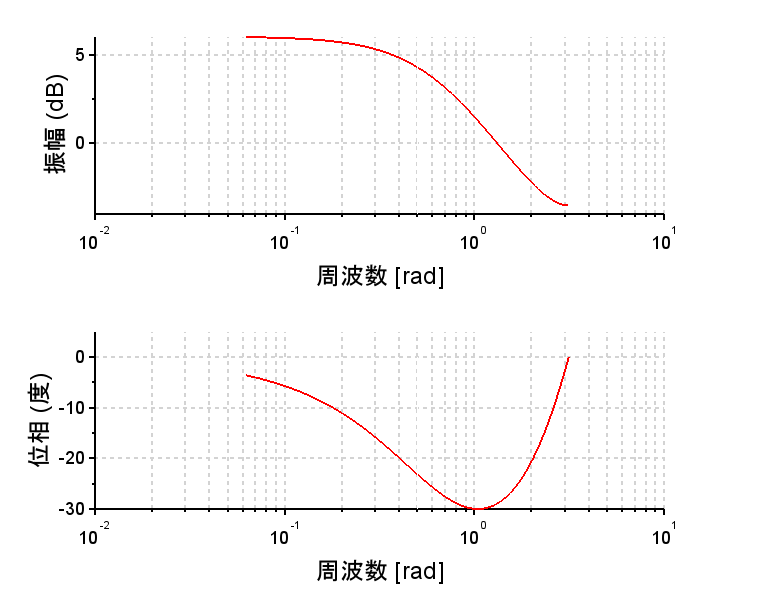
図２は、緑字のスクリプトによる結果である。横軸は\(\Omega \;[rad]\)で、Logスケール、振幅は「dB」、位相は「度」表示である。
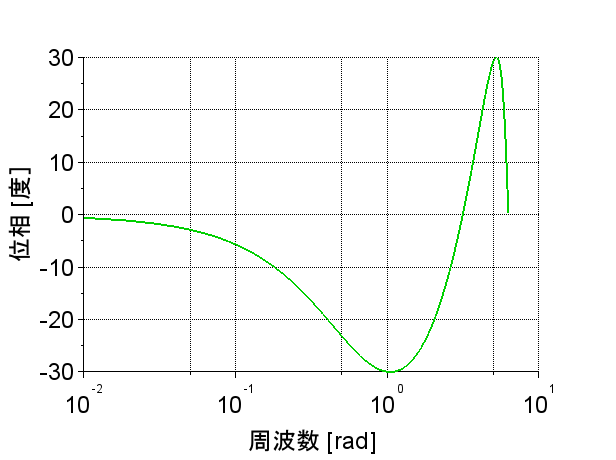
図３は、赤字のスクリプトによる結果である。図２と同じ結果がbode関数で簡単に得られる。ただし、ラジアン周波数は\(\pi\)までとなっている。図１からわかるように\(\pi\)以上は、折り返しになるだけなので、一般的に計算は不要である。