13. 電圧の測定法
電圧計は、ある2点間の電位差を測る電気計器である。指針形電圧計は、指針形電流計の原理を応用して作られており、電流計に抵抗値の大きな抵抗を接続することで、電流計に流れる電流を制限して、その電流計に微小に流れる電流を測定し、電圧に換算する。
指針形電圧計の内部には、磁針と磁場を発生させるコイルが組み込まれている。電圧計の端子に電圧を印加すると、電流が流れ、コイルに磁場が発生する。磁場が磁針に作用して、磁針が回転する。磁針の回転量は、印加された電圧の大きさに比例する。磁針の回転量を、目盛り付きのスケールによって電圧値に変換して表示する。
電圧計の測定範囲は、電圧計の内部に組み込まれている抵抗値によって決まり、抵抗値が大きいほど、電流計に流れる電流が小さくなり、電圧をより正確に測定することができる。電圧計は、電気回路の電圧を測定するために使用され、電気回路の故障診断や電気回路の設計・試作・施工等に使用される。
指針形電圧計の原理
直流電圧の測定
直流電圧を測定するには、直流電流計を応用する。図1に永久磁石可動コイル形電流計を電圧計として利用する構成を示す。なお、電流計部分は、内部抵抗\(R_m\)で表している。電流計には指針をフルスケールに動かす定格電流(最大電流)が決まっており、この電流を供給できる電圧が印可されるとき、それが電圧計の定格電圧(最大電圧)となる。
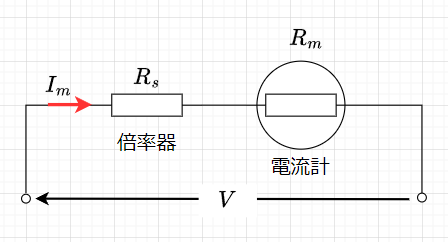
この定格電圧が決定できるように電流計に直列に抵抗\(R_s\)を挿入する。この抵抗\(R_s\)を倍率器と呼ぶ。この時、電圧方程式は、$$V = (R_s + R_m)\cdot I_m$$なので、倍率器の抵抗値\(R_s\)は、$$R_s = \frac{V}{I_m} - R_m $$であるが、\(R_s \gg R_m\)なので、$$R_s \approx \frac{V}{I_m}$$となる。ただし、この近似は確度の観点から決定する必要がある。
電圧計の内部インピーダンスの影響
図2に直流電圧計で電圧を測定する場合の概念図を示す。被測定電圧(測定したい電圧)を\(V_s\)とすると、DCV-Meterで測定される電圧\(V_d\)は、$$V_d = \frac{R_i}{R_s + R_i} V_s$$となる。従って、\(R_s\)に比べ\(R_i\)が十分に大きければ、\(V_d \approx V_s\)となり、ほぼ正確な電圧が測定できる。
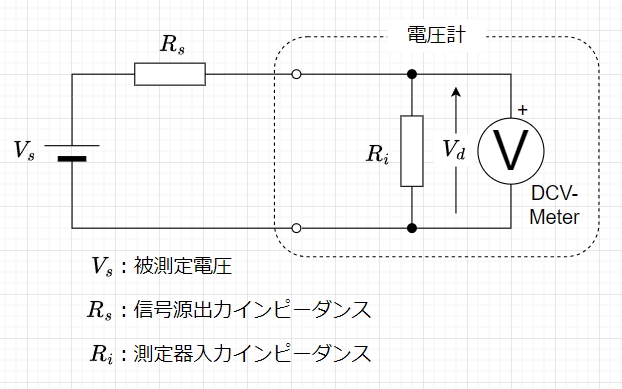
この時、誤差率\(\epsilon\)(実際の被測定電圧に対する測定電圧の誤差の割りあい)は、$$\epsilon = \frac{V_s - V_d}{V_s} \times 100 = \frac{V_s - \left(\frac{R_i}{R_s + R_i}\right) V_s }{V_s} \times 100 \\= \frac{R_s}{R_ s + R_i} \times 100\;[\%]$$で表せる。
一般的な電圧計(ディジタルマルチメータなど)では、内部抵抗は、数\(M\Omega\)程度であるが、高精度な電圧計では、内部抵抗\(R_i\)は\(10^{13} \;\Omega\)以上である。
交流電圧の測定
交流電圧計は、直流電流計から直流電圧計を構成したのと同様に、交流電流計から構成する。
交流電圧の測定で、大きな電圧を測定する場合には、抵抗での分圧、コンデンサでの分圧を使う。
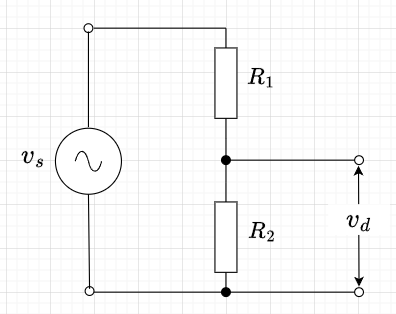
図3の抵抗での分圧では、測定電圧\(v_d\)は、$$v_d = \frac{R_2}{R_1 + R_2}v_s$$となる。よって、被測定電圧\(v_s\)は、$$v_s = \frac{R_1 + R_2}{R_2} v_d$$として求まる。
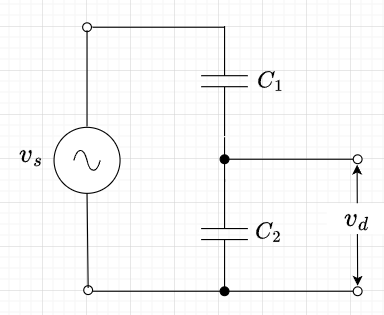
図4のコンデンサでの分圧では、各コンデンサの電荷\(Q\)は等しいので、$$Q =C_2 v_d ,\;\;\;Q= C_1(v_s - v_d)$$よって、測定電圧\(v_d\)は、$$v_d = \frac{C_1}{C_1 + C_2} v_s$$となる。よって、被測定電圧\(v_s\)は、$$v_s = \frac{C_1 + C_2}{C_1} v_d$$として求まる。
電圧測定による電流計測
電圧計で電圧を測定することで電流を計測する手法は、回路にシャント抵抗を挿入することで実現できる。図5はDCモータに通電している電流を計測する回路構成例である。DCモータの回路にシャント抵抗\(R_s\)を直列に挿入し、\(R_s\)の両端の電圧(電圧降下)を測定する。シャント抵抗\(R_s\)は、温度による変化が十分小さいこと、寄生インダクタンスが無視できること、が重要であり、また、回路への影響を小さくするために極力小さな抵抗値にする必要がある。この例では、数+\(m\Omega\)程度が妥当である。従って、\(R_s\)の電圧降下は非常に小さいので、増幅回路(この例では、オペアンプによる差動増幅器)で電圧降下を増幅し、\(V_{out}\)を電圧計で測定する。
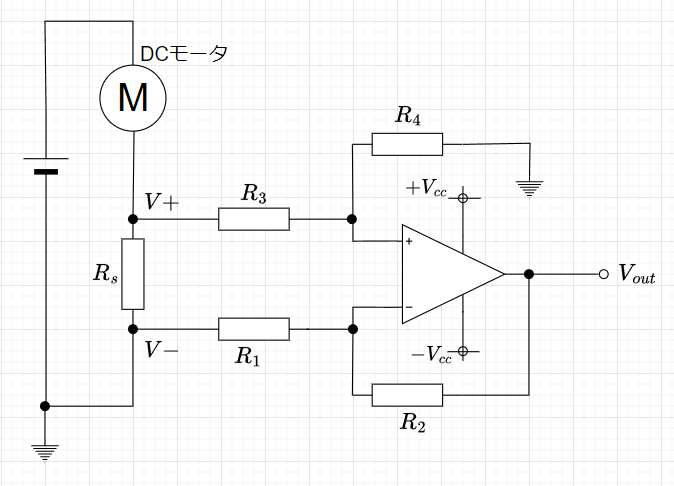
この例の差動増幅器の増幅度\(A_v\)は、$$A_v=\frac{R_2}{R_1}$$である。ただし、\(R_1=R_3 ,\;\;\; R_2 = R_4\)とする。従って、測定電流\(I\)は、$$I=\frac{V_{out}}{A_v}\cdot\frac{1}{R_s}$$となる。
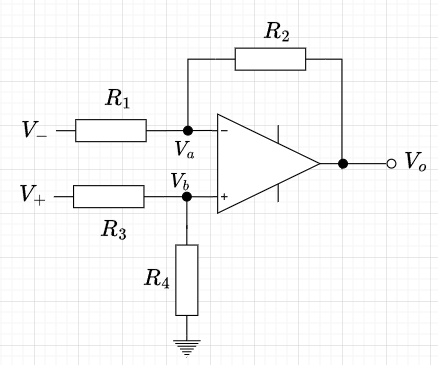
差動増幅器の増幅度
右図に示す差動増幅器の増幅度を求める。
オペアンプの理想基本特性(入力インピーダンスは\(\infty\))より、$$V_b = \frac{R_4}{R_3 + R_4} V_{+} \\ \frac{V_{-} - V_a}{R_1} = \frac{V_a -V_o}{R_2}$$が成立する。ここで、バーチャルショートより、\(V_a = V_b\)を使って、式を整理すると、$$V_o = \left(\frac{R_1 + R_2}{R_1}\right) \left(\frac{R_4}{R_3 + R_4}\right) V_{+} - \frac{R_2}{R_1} V_{-}$$となる。ここで、\(R_1 = R_3\)、\(R_2 = R_4\)とすると、$$V_o = \frac{R_2}{R_1}(V_{+} - V_{-})$$となる。つまり、2つの入力\(V_{+}\)と\(V_{-}\)の差を\(R_2/R_1\)倍することになる。