14-2. ベッセルフィルタ
ベッセルフィルタは、群遅延が最大限平坦になるようにしたアナログフィルタである。
位相特性が線形になるため、方形波などの波形を入力しても、歪みの少ない出力波形を得ることができる。
※群遅延:周波数によって信号の伝搬時間が変わる現象。群遅延\(\tau_g\)は、入力波形と出力波形の位相差\(\phi\)を角周波数\(\omega\)で微分することで求められる。\(\tau_g = -\frac{d \phi}{d\omega}\)
以下にベッセルフィルタの特徴をまとめる。
・群遅延の平坦性: すべての周波数成分が同じ遅延時間を持つことを意味し、方形波などの波形を入力しても、歪みの少ない出力波形を得ることができる。
・減衰特性:ベッセルフィルタの減衰特性は、バターワースフィルタよりも緩やかである。
ベッセルフィルタは、次数によって分類され、次数が高くなるほど、群遅延の平坦性が高くなり、減衰特性の傾きが急になる。2次のベッセルフィルタが、 多くの用途で用いられる一般的なベッセルフィルタで、群遅延の平坦性と減衰特性のバランスが良い。
ベッセルフィルタは、群遅延が平坦で 波形の歪みを最小限に抑えることができ、入力信号に急激な変化があっても、出力信号に過渡的な振動が発生しにくいという利点がある。しかし、バターワースフィルタに比べて、通過帯域における周波数特性に多少の揺らぎがあり、 バターワースフィルタよりも減衰特性が緩やかである。また、バターワースフィルタに比べて設計が複雑である。
正規化フィルタ
アナログフィルタ回路の設計は、伝達関数の設計から行うことが多い。基本的なフィルタ回路を使用する場合、その伝達関数は 良く知られおり、正規化されている式も多くある。
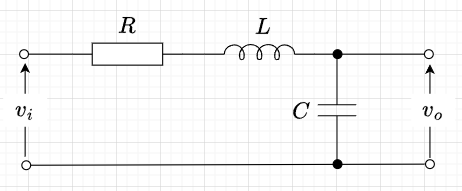
正規化とは、例えば図1の2次系RLC回路の伝達関数は、$$G(s) = \frac{1}{LCs^2 + RCs + 1} =\frac{\frac{1}{LC}}{s^2 + \frac{R}{L}s + \frac{1}{LC}}$$であり、\(\omega_0 = \frac{1}{\sqrt{LC}}\)、\(\zeta = \frac{R}{2}\sqrt{\frac{C}{L}} \)とおくと、この2次系伝達関数は、$$G(s) = \frac{\omega_0^2}{s^2 + 2\zeta \omega_0 s +\omega_0^2}$$となる。さらに、\(s \rightarrow j\omega\)として、周波数伝達関数をもとめると$$G(j \omega) = \frac{\omega_0^2}{(\omega_0^2 - \omega^2) +j 2\zeta \omega_ 0 \omega}$$となる。ここで、分母分子を\(\omega_0^2\)で割ると、$$G(j \omega) = \frac{1}{1 - \left(\frac{\omega}{\omega_0}\right)^2 + j 2 \zeta \left(\frac{\omega}{\omega_0}\right)}$$となる。\(\frac{\omega}{\omega_0}\)を正規化角周波数(正規化周波数)、この周波数伝達関数を正規化周波数伝達関数と呼び、このようにしてフィルタの周波数伝達関数を正規化したフィルタを正規化フィルタという。
図2は正規化5次LPFの回路構成例である。また、バタワースLPFとベッセルLPFの各係数を表1に示す。
※フィルタの各係数は、文献やこちらを参考にして下さい。
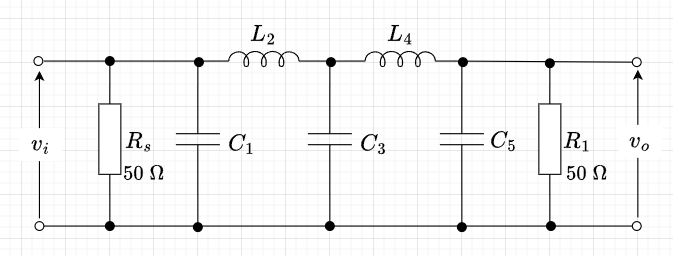
| \(R_s\) | \(C_1\) | \(L_2\) | \(C_3\) | \(L_4\) | \(C_5\) | |
| バタワース型 | 1.0000 | 0.6180 | 1.6180 | 2.0000 | 1.6180 | 0.6180 |
| ベッセル型 | 1.0000 | 0.1743 | 0.5072 | 0.8040 | 1.1110 | 2.2582 |
遮断周波数\(f_c = 100 \;kHz\)、入力インピーダンスを\(R_s=1.0000 \times 50 =50\; \Omega\)とした5次ベッセルLPFを設計する。$$\omega_c = 2\pi f_c = 6.2832\times 10^5\; rad/s $$
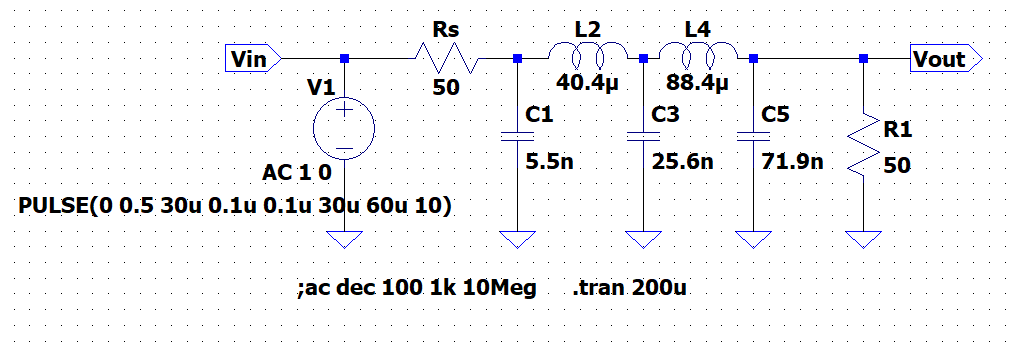
LTspice
$$C1 = \frac{0.1743}{\omega_c \times 50} = 5.5\; nF, \;\;\;\;\;\; L2 = \frac{0.5072 \times 50}{\omega_c}= 40.4 \;\mu H \\ C3 = \frac{0.8040}{\omega_c \times 50} = 25.6 \; nF, \;\;\;\;\;\; L4 = \frac{1.1110 \times 50}{\omega_c} = 88.4 \;\mu H, \;\;\;\;\;\; C5 = \frac{2.2582}{\omega_c \times 50} = 71.9 \;nF $$である。図3に回路図を示す。
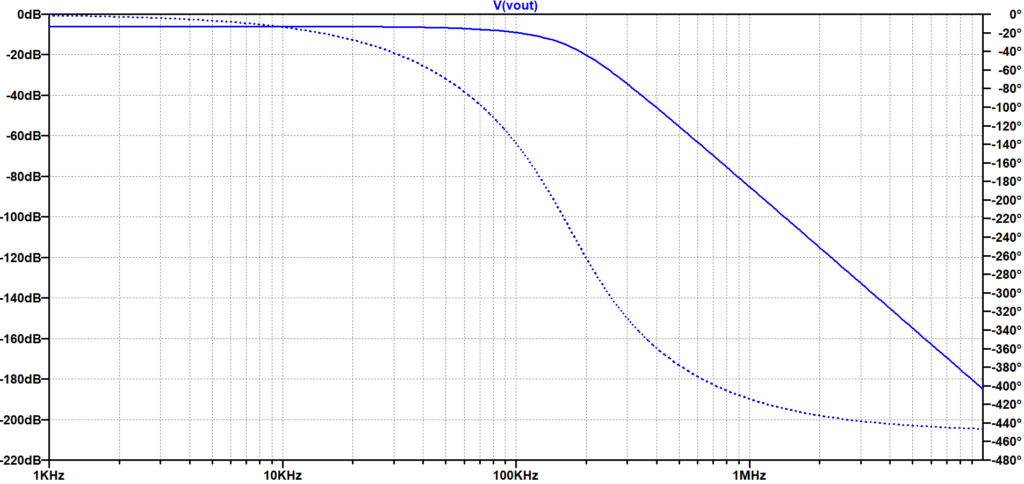
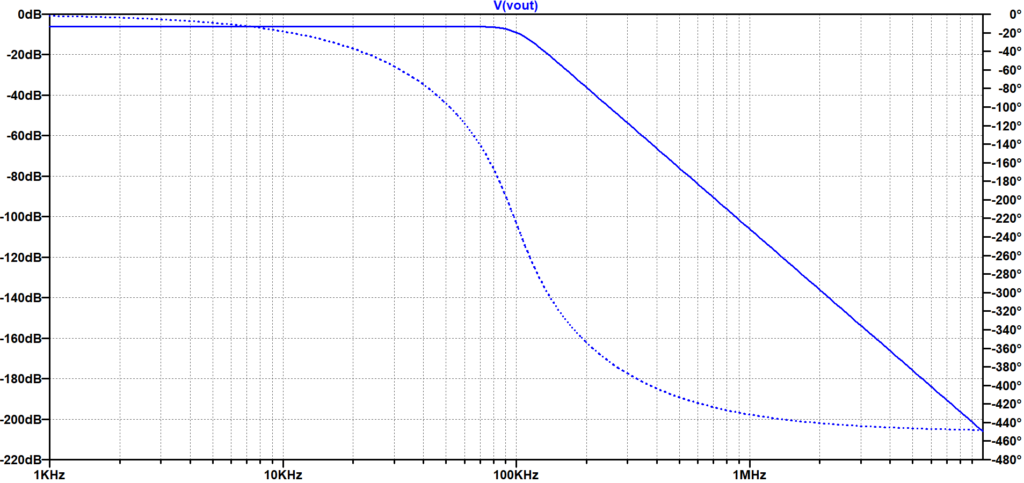
図4に5次ベッセルLPFの周波数特性を示す。図5は、周期\(60\;\mu s\)(周波数:\(16.7\;kHz\))の矩形波を入力(赤線)したときの出力信号(青線)を示す。図9の5次バタワースLPFの時間応答特性と比較すると、波形の振動が小さく、位相ずれも小さい。さらに、図6は、周期\(20\;\mu s\)(周波数:\(50.0\;kHz\))の矩形波を入力(赤線)したときの出力信号(青線)を示す。図10の5次バタワースLPFの時間応答特性では、ほぼ基本波の正弦波状となり、位相も大きく遅れているのに対して、図6の5次ベッセルLPFの場合は、矩形波の形状をある程度保ち、位相遅れも小さい。以上のことから、バタワースLPFよりベッセルLPFの方が、矩形波の伝送に適していることがわかる。但し、図4のベッセルLPFと図8のバタワースLPFの周波数特性を比較して分かるように、高域での減衰特性がベッセルLPFの方が緩やかであるため、高域の雑音抑圧特性は弱いことになる。
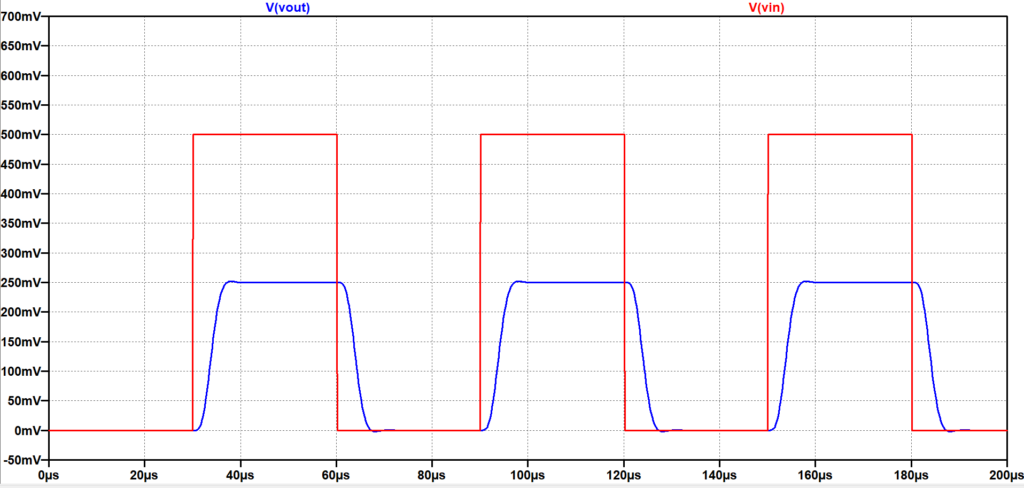
入力\(16.7\;kHz\)(赤)
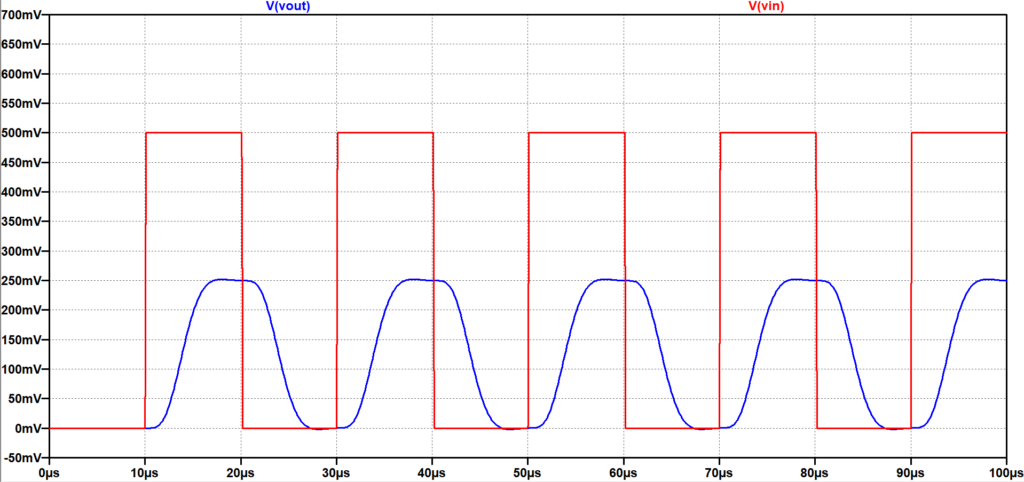
入力\(50\;kHz\)(赤)
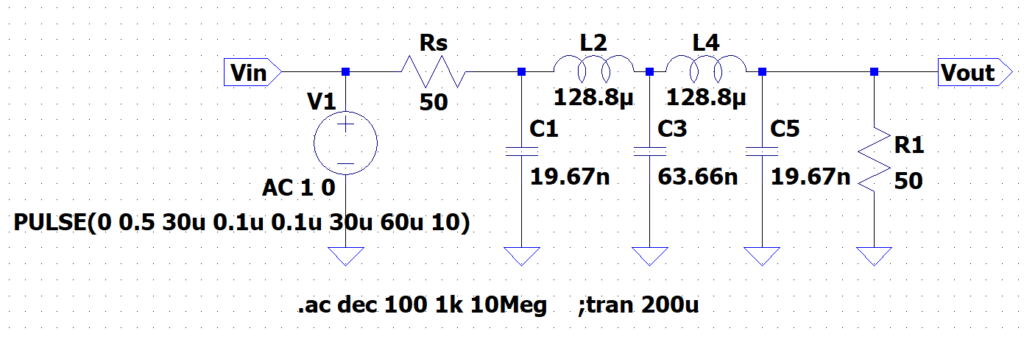
図6は、図3と同じ遮断周波数\(f_c = 100 \;kHz\)、入力インピーダンスを\(R_s=1.0000 \times 50 =50\; \Omega\)としたときの5次バタワースLPFの回路図である。
LTspice
$$C1 = \frac{0.6180}{\omega_c \times 50} = 19.67\; nF, \;\;\;\;\;\; L2 = \frac{1.6180 \times 50}{\omega_c}= 128.8 \;\mu H \ C3 = \frac{2.0000}{\omega_c \times 50} = 63.66 \; nF, \;\;\;\;\;\; L4 = L2 = 128.8 \;\mu H, \;\;\;\;\;\; C5 = C1 = 19.67 \;nF $$である。図7に回路図を示す。図8がその周波数特性、図9,10が時間応答特性である。
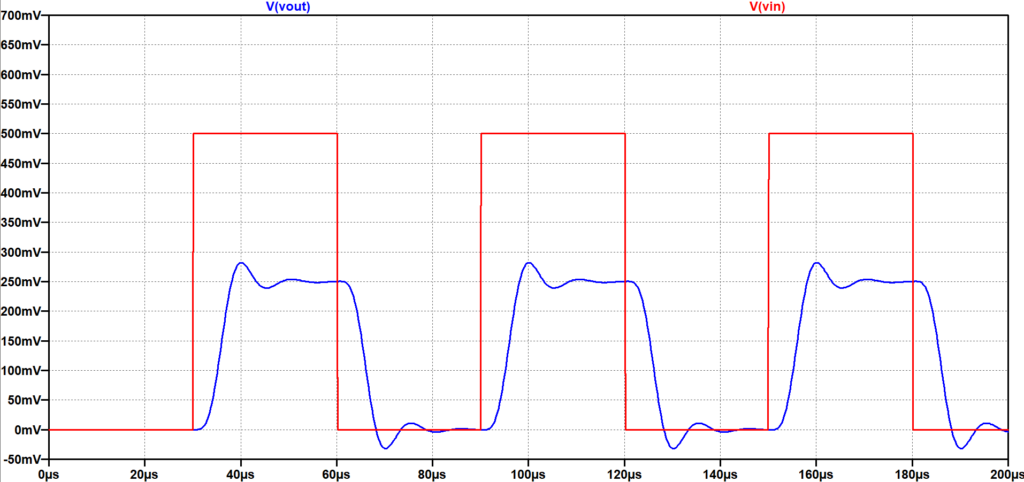
入力\(16.7\;kHz\)(赤)
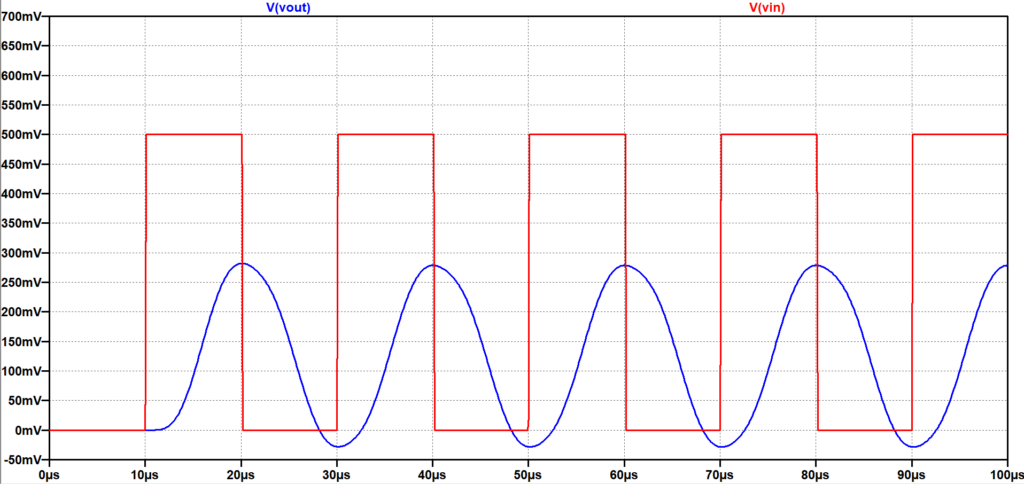
入力\(50\;kHz\)(赤)

